Алгебраическое интерполирование

Рассмотрим функцию , , для которой известны ее значения в точках:

Точки известны и расличны между собой.

Будем аппроксимировать функцию алгебраическим полиномом:

(1)

Тогда неизвестные константы определяются из следующей системы:

(2)

Следует отметить, что при вычисление коэффициентов из системы (2) приводит к катастрафическому искажению их значений из-за возрастающей вычислительной погрешности. Поэтому на практике используют другие виды интерполяции.

Интерполяционный многочлен Лагранжа

Рассмотрим функцию , , для которой известны ее значения в точках:

Точки известны и расличны между собой.

Интерполяционным многочленом Лагранжа называется следующий многочлен:

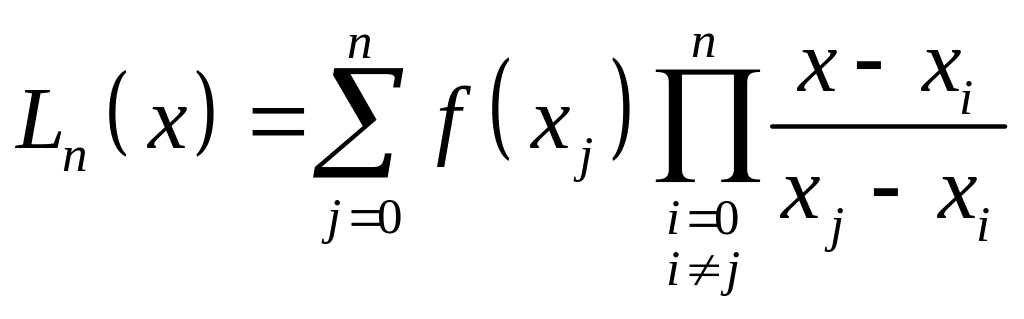
Многочлены Чебышева

Многочленом Чебышева называется многочлен, задаваемый формулой и определенный на промежутке [-1,1].

Погрешность интерполяции можно уменьшить путем выбора узлов интерполяции. Погрешность будет минимальной, если в качестве узлов интерполяции взять корни многочленов Чебышева:

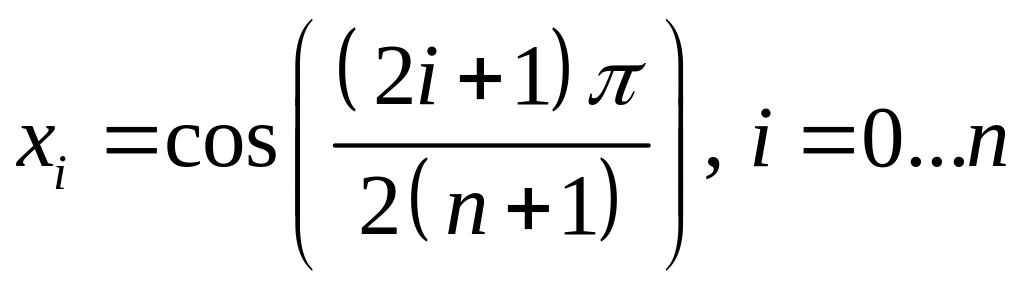(на отрезке [-1,1])

Для произвольного отрезка получим

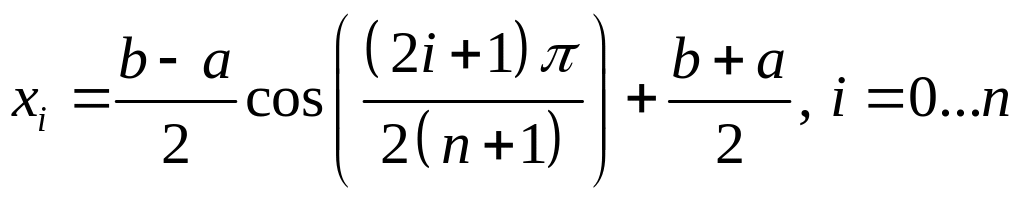
Разделенные разности и многочлен Ньютона

Пусть ‑ произвольные неповторяющиеся узлы.

Числа

называются разделенной разностью первого порядка функции в точках .

Разделенные разности -го порядка определяются через разделенные разности -го порядка с помощью реккурентной формулы:

Справедливо равенство

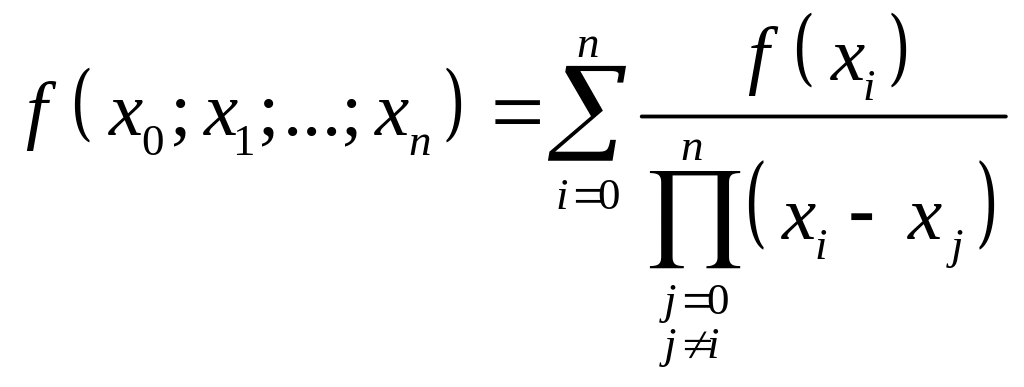
Интерполяционным многочленом Ньютона для неравных промежутков называется многочлен

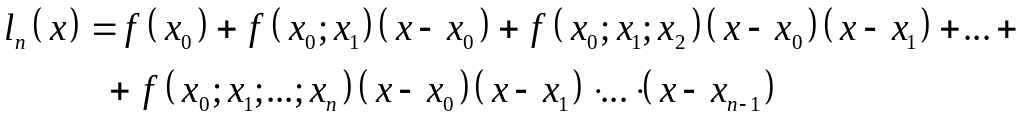
Функции для постоение различных интерполяционных полиномов объединены в пакете CurveFitting, т.е. для их использования необходимо сначала подключить данный пакет командой

> with(CurveFitting);

После выполнения данной команды в области вывода появится список всех команд этого пакета.

Полиномиальная интерполяция выполняется с помощью функции:

PolynomialInterpolation(координаты_х, координаты_y, переменная, параметр)

Где координаты_х и координаты_y – координаты точек в виде списков [x1, x2, ..., xn] и [y1, y2, ..., yn] соответственно. Переменная – имя переменной, от которой будет зависить будущий полином. параметр – какого вида полиномы используются, задается в виде form=значение, где значение может быть Lagrange (Лагранжа), Newton (Ньютона) или power (алгебраическими полиномами).

Решение уравнений, неравенств и их систем

Команда solve() системы Maple является универсальным средством, позволяющим решать алгебраические уравнения, неравенства и их системы.

Точно так же, как и при задании уравнений, два выражения, соединенные знаками >= (больше или равно), <= (меньше или равно), > (больше) или < (меньше), представляют новый тип — неравенство (inequation).

Команда solve()

Команда solve() позволяет решать уравнения и системы уравнений, неравенства и системы неравенств. Она всегда пытается найти замкнутое решение в аналитической форме.

solve(уравнение, переменная);

solve({уравнение1, уравнение2,...},{переменная1, переменная2,...});

Первая форма команды предназначена для решения одного уравнения относительно заданной переменной, тогда как вторая форма позволяет решать системы уравнений относительно переменных, заданных вторым параметром. Если не задана переменная/переменные, относительно которых следует решать уравнение/систему уравнений, то Maple выдаст все решения относительно всех неопределенных переменных в исходных уравнениях.

Пример. Решение уравнений и систем уравнений

> eq:=x^2-2*x+y^2=0;

> solve(eq,x);

> solve({eq},x);

> eq2:=x+y=0;

> solve({eq,eq2},{x,y});

> solve(eq);

Когда Maple не может найти ни одного решения, то команда solve() возвращает пустую последовательность NULL. Это означает, что, либо решения не существует, либо Maple не удалось его найти.

Решение последнего уравнения из примера осуществлялось без указания переменной, относительно которой следовало решать уравнение. Maple решил их относительно всех неизвестных величин, входящих в уравнение.

В общем случае полиномиальное уравнение степени выше 4 может не иметь решения, выраженного с помощью радикалов. В этом случае для представления результатов Maple использует специальную функцию RootOf(), которая применяется для обозначения любого корня выражения, заданного в качестве ее параметра:

> solve(cos(x)=x,x);

> evalf(%);

В этом примере функция RootOf(_Z-cos(_Z)) представляет любое решение уравнения _Z-cos(_Z)=0. Обратим внимание на переменную _Z. Это системная переменная, сгенерированная Maple, которая всего лишь заменяет переменную х нашего уравнения. С помощью функции evalf() можно получить приближенные числовые значения функции RootOf.

Графическое решение данного уранения можно получить путем построения графиков функций и . Для этого можно воспользоваться командой plot, которая имеет следующий синтаксис:

plot(функция, переменная=диапазон, параметры);

или для построения нескольких графиков:

plot([функция1, функция2, … , функцияN], переменная=диапазон, параметры);

Где функция – функция от независимой переменной, переменная – это имя независимой переменной, диапазон – диапазон изменения независимой переменной (не является обязательным параметром), задается в виде a..b, параметры – необязательные параметры, имеют синтаксис имя_параметра=значение, например, задание цвета color=red. При построении графиков нескольких функций обычно используют опцию legend, которая показывает легенду, т.е. какая кривая какой функции соответствует.

Построим функции и на графике:

> y1:=cos(x);

y2:=x;

> plot([y1,y2],x=-2*Pi..2*Pi, legend=[“косинус”,”прямая y=x”]);

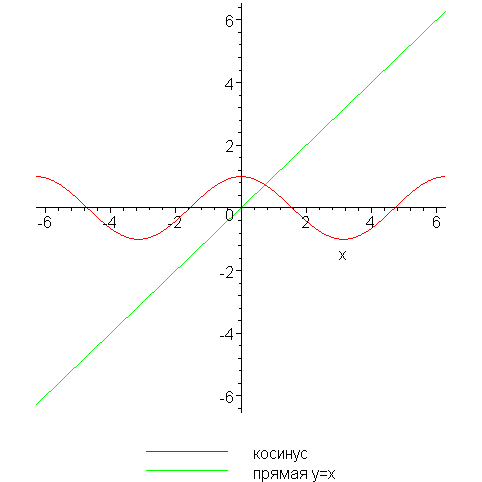
Особо отметим решение с помощью команды solve() тригонометрических уравнений. По умолчанию Maple решает их на промежутке . Для получения всех решений тригонометрических уравнений следует задать значение глобальной переменной _EnvAllSolutions равным true.

> eq:=cos(x)=0;

> solve(eq,x);

> _EnvAllSolutions:=true;

> solve(eq,x);

Как видно, в случае _EnvAllsolutions:=true Maple действительно строит все решения тригонометрического уравнения с использованием целочисленной системной переменной _Z1~, в которой знак тильда (~) означает, что на значения переменной наложены некоторые ограничения. В данном случае эта переменная может принимать только целочисленные значения. В этом можно убедиться, выполнив команду about(_Z1~).

Команда solve() может решать неопределенные системы уравнений, в которых количество уравнений меньше числа неизвестных. В этом случае система Maple сама решает, какие из неизвестных принять за параметры, а какие за неизвестные, относительно которых следует строить решение.

> eq:=x^2-2*x+y^2=0;

> solve(eq,x);

> x1:=%[1];

Для того, чтобы получить функцию своих переменных следует воспользоваться командой unapply(), которая преобразует выражение в функцию. Первым параметром задается само выражение, а последующие определяют, от каких переменных эта функция будет зависеть:

> x:=unapply(x1,y);

> x(1);

Если при решении систем уравнений ответ получается в виде множества уравнений, в которых левая часть является неизвестной переменной, то для того, чтобы присвоить найденные значения переменным, относительно которых решалась система, следует применять команду assign(). Эта команда присваивает переменным, стоящим в левой части уравнений из множества решений, значения, равные правым частям.

> eqns:={x+2*y=3,y+x=1};

> sols:=solve(eqns);

> assign(sols);

> x;

> y;