Подстановка и преобразование выражений

При выполнении математических преобразований часто необходимо произвести замену переменных в выражении, функции, уравнении и т. д. Для этих целей в Maple существует команда subs(), синтаксис которой имеет следующий вид:

subs(старое_выражение=новое_выражение, выражение);

Пример. Подстановки в выражении

> ex:=x^2+x^(1/3);

> subs(x=cos(x),ex);

> subs(x=1,ex);

Иногда необходимо выполнить преобразование выражения одного типа в другой тип. Например, нельзя строить график ряда Тейлора какой-либо функции, но всегда можно построить график полинома. Следовательно, следует выражение, имеющее тип series (ряд), преобразовать в выражение, имеющее тип polynom (полином). Преобразовать выражение в другой тип можно командой convert(), первым параметром которой задается выражение, а вторым — тип, в который это выражение следует преобразовать.

Практическое задание

Дано уравнение

Его корни определяются по формулам

(1)

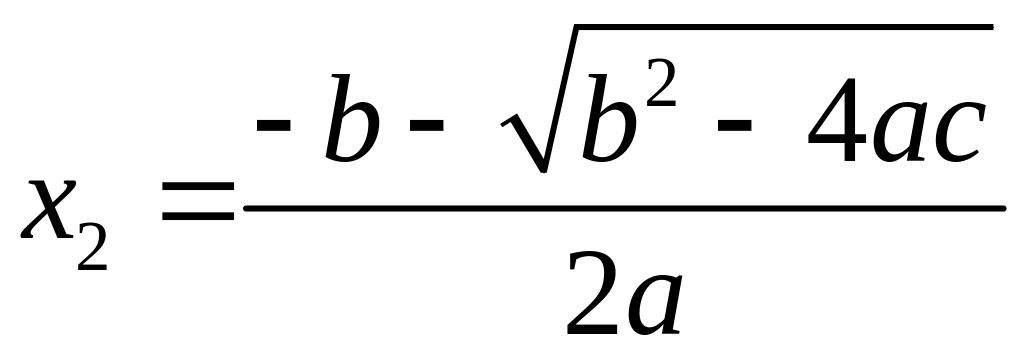
Для данного примера формула для вычисления первого корня имеет большую погрешность, т.к. в числителе стоит разность близких чисел. Поэтому для вычисления этого корня необходимо избавится от этой разности:

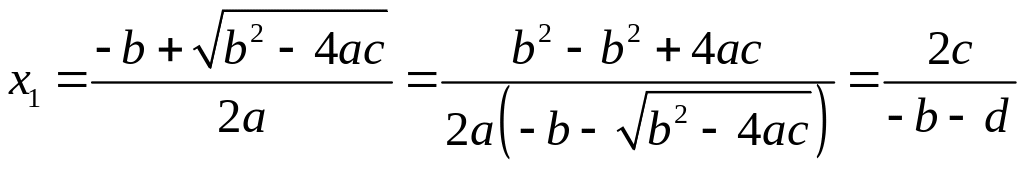(2)

В Maple необходимо сделать следующее:

1. Задать количество значащих цифр 4

2. Записать коэффициенты уравнения как переменные a, b, c.

3. Записать уравнение и обозначить его переменной eq.

4. Отдельно посчитать корень из дескреминанта и обозначить его переменной d (получить значение в виде числа с плавающей точкой).

5. Посчитать первый корень по формуле (1) и запомнить его в переменную x11 (получить его десятичное представление).

6. Подставить полученное значение x11 в уравнение eq и запомнить полученное значение как y11.

7. Посчитать первый корень по формуле (2) и запомнить его в переменную x12 (получить его десятичное представление).

8. Подставить полученное значение x12 в уравнение eq и запомнить полученное значение как y12.

9. Проанализировать полученные результаты y11 и y12.

10. Проделать пункты 2-9 для 8 цифр в мантиссе.

11. Проанализировать полученные результаты.

Занятие 2. Приближение функций

Для вычисления стандартных функций, таких как , , и , в пакетах прикладных программ используются вычислительные процедуры, включающие в себя приближение полиномами.

Приближение полиномом Тейлора

Предположим, что функция имеет непрерывные производные до порядка на и некоторая точка из этого промежутка. Тогда

Недостатком этого приближение является необходимость вычисления функции и ее производных в точке , которые не всегда известны.

Приближение функий заданных таблицей своих значений

Простейшая задача, приводящая к приближению функций, заключается в следующем. В дискретные моменты времени наблюдаются значения фунции ; требуется восстановить ее значения при других .

Иногда из каких-то дополнительных соображений известно, что приближающую функцию следует искать в виде

Если параметры определяются из условия совпадения функции и приближающей функции в точках , которые называются узлами интерполяции

то такой способ приближения называют интерполяцией или интерполированием.

Если точка , в которой необходимо вычислить значение функции , лежит вне отрезка , где и соответственно минимальное и максимальное значение узлов интерполяции, то такая операция называется экстраполяцией.

Способы интерполирования отличаются выбором вида аппроксимирующей функции .