Команды преобразования выражений

Синтаксис вызова стандартной команды следующий:

команда(пар_1, пар_2,…, пар_n);

Здесь команда ‑ это имя вызываемой функции, a пap_1, пар_2,... означают необходимые для выполнения команды параметры, которые могут быть переменными или даже выражениями, причем их тип должен соответствовать типу параметров используемой функции.

Система обозначений функций в Maple интуитивно проста, поэтому обыкновенно имя функции соответствует действию, которое она выполняет (все имена заданы на английском языке).

Наиболее употребляемые команды Maple расположено в ядре системы, для их вызова необходимо лишь написание имени команды. Остальные команды и функции объединены в пакеты. Для вызова таких команд необходимо сначала подключить соответсвующий пакет командой with(имя_пакета);.

Упрощение выражения: simplify()

Команда simplify() предназначена для упрощения разнообразных выражений. Ее синтаксис имеет следующий вид:

simplifу(выражение);

В скобках в качестве параметра передается выражение, подлежащее упрощению.

При упрощении выражения можно предположить, что все переменные в нем являются, например, положительными, или принадлежат некоторому отрезку действительных чисел. Это осуществляется заданием ключевого параметра assume=свойство. Форма вызова команды в этом случае имеет вид:

simplify(выражение,assume=свойство);

где параметр свойство может принимать одно из следующих значений: complex – комплексная область, real – действительная область, positive – положительные действительные числа, integer – целые числа, RealRange(a,b) –интервал (а,b) действительных чисел.

Пример. Упрощение выражений

> f:= ln(exp(x));

> simplify(f);

> simplify(f, assume=real);

> a:=1/sqrt(5)*(((1+sqrt(5))/2)^3-((1-sqrt(5))/2)^3);

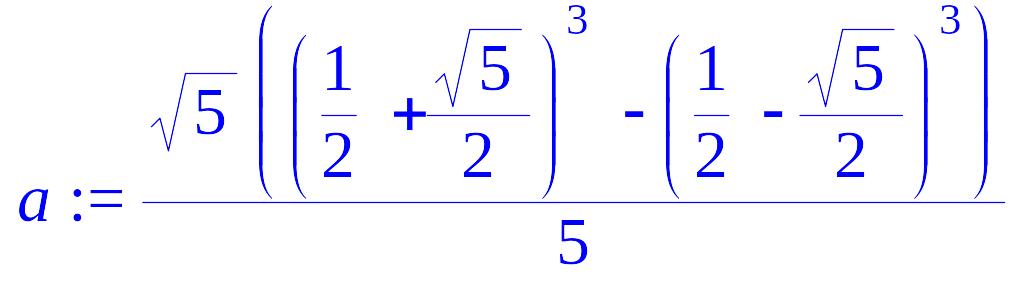
> simplify(a);

Обратим внимание на упрощение выражения f. Использование команды без параметров не упростило выражения , тогда как второй оператор с предположением о действительной области изменения переменной х упростил заданное выражение. При упрощении Maple предполагает, что там, где это возможно, переменные изменяются в области комплексных чисел.

Пример. Упрощение с предположением

> f:=sqrt(x^2);

> simplify(f);

> simplify(f,assume=real);

> simplify(f,assume=positive);

Раскрытие скобок в выражении: expand()

Основное назначение команды expand() ‑ раскрытие скобок в выражении.

expand(выр);

где выр является выражением, в котором необходимо раскрыть скобки.

Пример. Представление произведений в виде суммы

> expand((x+1)*(x+2));

> expand(sin(x+y));

> expand(exp(a+ln(b)));

Разложение полинома на множители: factor()

Основное предназначение команды factor() – разложить на множители полином от нескольких переменных.

> factor(x^3*y-x^3*b-x^2*a*y+x^2*a*b+2*x^2*y^2-2*x^2*y*b-2*x*y^2*a+2*x*y*a*b+y^3*x-y^2*x*b-y^3*a+y^2*a*b);

Пример. Разложение полинома над разными полями

> factor(x^3+2);

> factor(x^3+2.0);

> factor(x^2-1);

Ограничения на неизвестные: assume()

Команда assume() накладывает ограничения на неизвестные величины Maple. Она имеет следующий синтаксис:

assume(х, свойство);

Здесь х представляет любую неопределенную переменную Maple или выражение с такими переменными, а параметр свойство может принимать значения, равные названиям свойств (специальным символьным именам, зарезервированным системой Maple для задания разнообразных ограничений на переменную или выражение, определенные первым параметром), имени типа данных и числовому диапазону. Некоторые из наиболее употребительных свойств перечислены в таблице (полный список в справке).

Таблица. Свойства числовых переменных и выражений

Название свойства	Описание
negative	Отрицательные вещественные числа из интервала (нуль не включается)
nonnegative	Неотрицательные вещественные числа из интервала (нуль включается)
positive	Положительные вещественные числа из интервала (нуль не включается)
posint	Целые строго большие 0
odd	Нечетные числа
even	Четные числа
complex	Комплексные числа
real	Вещественные числа
rational	Рациональные числа (дроби и целые)
integer	Целые числа

Пару параметров (x,свойство) можно заменить математическим отношением. Например, (x,negative) соответствует отношению x<0 и т.д.

Команда assume() может получать несколько пар (x, свойство) или математических отношений в качестве своих параметров:

> assume(x>1,х<2);

т.е. переменная x может изменяться только в интервале (1,2).

Новое ограничение, накладываемое новой командой assume() на переменную, отменяет все предыдущие ограничения.

Для снятия всех наложенных ранее на переменную предположений следует этой переменной просто присвоить ее же символьное имя (имя переменной, заключенное в одинарные кавычки):

> х:='х';

Команда about() отображает информацию о наложенных ограничениях на неизвестную величину:

> about(x);

Originally x, renamed x~:

is assumed to be: RealRange(Open(1),2)