Методы Рунге-Кутта

Наиболее популярен метод Рунге-Кутта порядка . Он вполне точен, стабилен и прост для программирования. Метод основан на вычислении :

где

Данную схему называют стандартной или классической.

Системы дифференциальных уравнений

Задача Коши:

Метод Эйлера:

для

Метод Рунге-Кутта порядка 4:

где

Решение обыкновенных дифференцильных уравнений в Maple

Для решения дифференцильных уравнений и их систем можно воспользоваться командой dsolve() или функциями пакета DEtools. Общий синтаксис команды решения дифференциального уравнения следующий:

Dsolve(уравнения, неизвестные, [опции]);

Уравнения – одно или несклько уравнений (система). Если это система, то уравнения должны быть представлены в виде множества.

неизвестные ‑ неизвестная функция/фукнции. Если их несоклько, то тоже в виде множества.

опции ‑ необязательные опции в виде название=значение.

Производную можно задать с помощью функции diff и оператора D, причем саму неизвествную функцию следует определять явням указанием независимой переменной, например y(x).

Оператор дифференцирования имеет следующий синтаксис:

(D@@n)(функция)(переменная);

n ‑ целое число, определяющее порядок производной.

функция ‑ используемый идентификатр функции

переменная ‑ независимая переменная функции.

Например, производную второго порядка фукнции f(x) следует задавать следующим образом:

(D@@2)(f)(x);

Пример. Решение дифференциального уравнения

> ode := diff(y(x),x,x) = 2*y(x) + 1:

> dsolve(ode,y(x));

> ics := y(0)=1, D(y)(0)=0;

> dsolve({ode,ics},y(x));

Если точное решение задачи Коши система Maple не смогла найти, то можно построить численное решение с использованием все той же команды. Для этого следует задать опцию type=numeric, а с помощью опции method=метод определить используемый для построения численного решения метод. Парамет метод может принимать одно из значений

Rkf45 – метод Рунге-Кутта-Фальберга порядка 4-5 (задан по умолчанию)

Dverk78 – метод Рунге-Кутта порядка 7-8

Пример. Численное решение дифференциального уравнения

> ode:=diff(y(x),x,x)+y(x)=0;

> F:=dsolve({ode,y(0)=0,D(y)(0)=1},y(x),type=numeric);

> F(1);

> F(2);

Процедура численного решения выдает результат в виде списка значений независимой переменной, самой фукнции и ее производных (до порядка на 1 меньше порядка уравнения).

Отобразить это решение на графике можно с помощью команды odeplot пакета plots:

> plots[odeplot](F,[x,y(x)],-5..5);

Некоторые команды пакета DEtools:

DEplot() и DEplot3d() – для построения графиков решения дифференциальных уравнений и их систем.

dfieldplot() – отображение поля направлений.

phaseportrait() – отображения фазового портрета.

Пример. Использование команд пакета DEtools

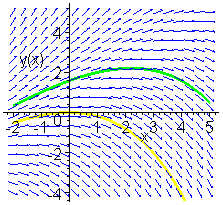
> DEplot(cos(x)*diff(y(x),x$3)-diff(y(x),x$2)+Pi*diff(y(x),x)=y(x)-x,y(x),

x=-2.5..1.4,[[y(0)=1,D(y)(0)=2,(D@@2)(y)(0)=1]],y=-4..5);

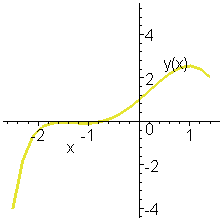
> dfieldplot(Pi*diff(y(x),x)=y(x)-x, y(x), x=-3..3,

y=-3..2);

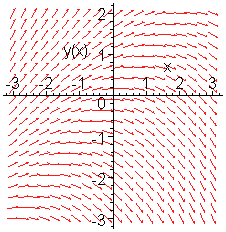
> phaseportrait(Pi*diff(y(x),x)=y(x)-x,y(x),x=-2..5,[[y(0)=0],[y(1)=2]],y=-4..5,colour=blue,linecolor=[yellow,green]);