Решение систем линейных уравнений

В пакет LinearAlgebra входит специальная команда LinearSolve() решения систем линейных алгебраических уравнений. В качестве параметров ей передаются матрица A системы и вектор правых частей b. Сама система в матричной форме записывается в виде Ax=b.

Практическое задание 1.

Найти решение системы с помощью обратной матрицы и проверить его командой LinearSolve.

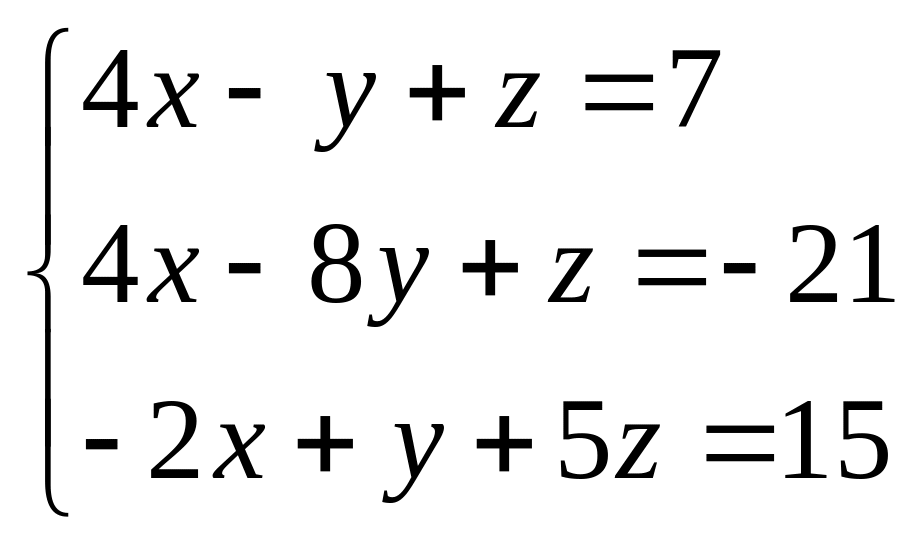
План решения:

1. Подключить покет LinearAlgebra

2. Задать матрицу A и вектор b

3. Найти обратную матрицу для A

4. Найти решение уравнения

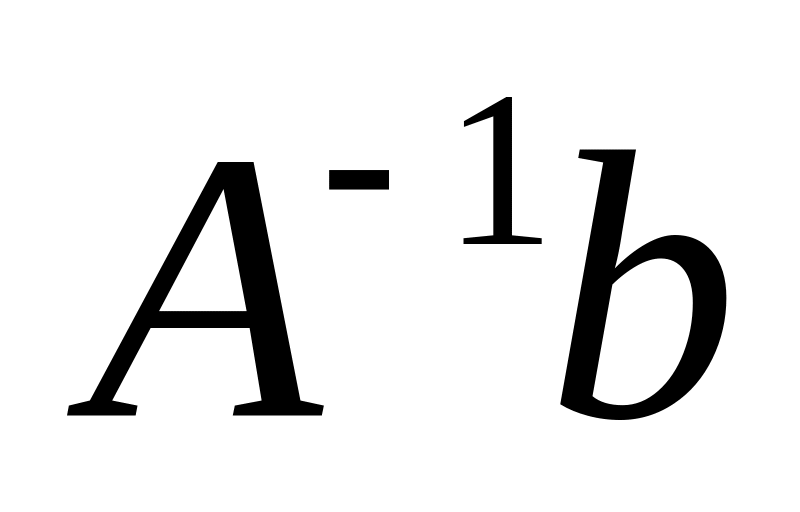
5. Найти решение с помощью команды LinearSolve

Практическое задание 2

Найти решение нелинейной системы методом итераций

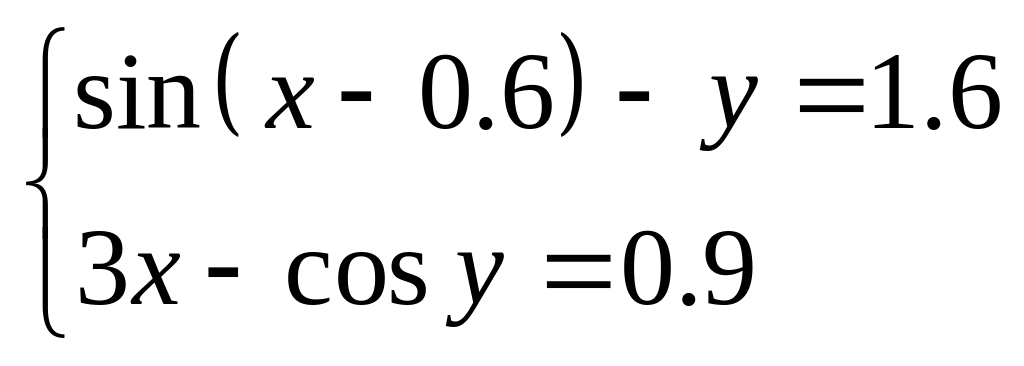
План решения:

1. Записать два уравнения.

2. Выразить из первого уравнения 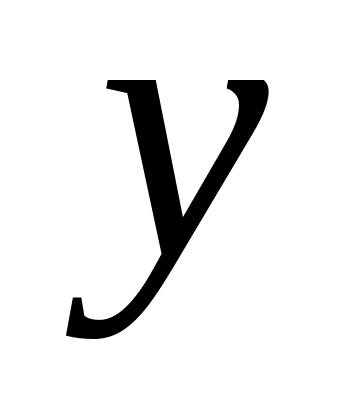(обозначить F через ), а из второго (обозначить G через )

3. Построить графики этих функций, используя функцию implicitplot пакета plots

4. Выбрать начальное приближение и 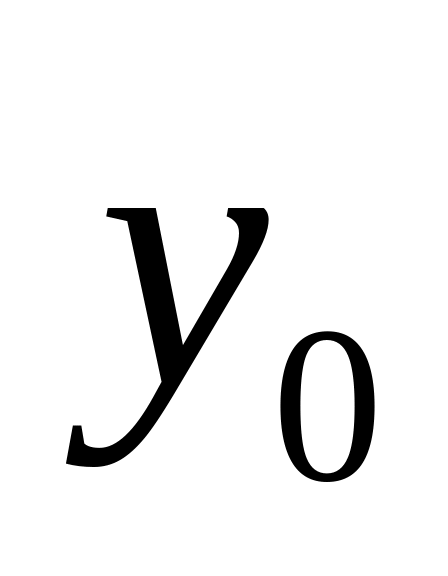из графика, обозначить x[0] и y[0]

5. Задать погрешность вычислений

6. Найти решение путем итераций по формуле . Т.е. написать цикл, выход из которого осуществляется когда и .

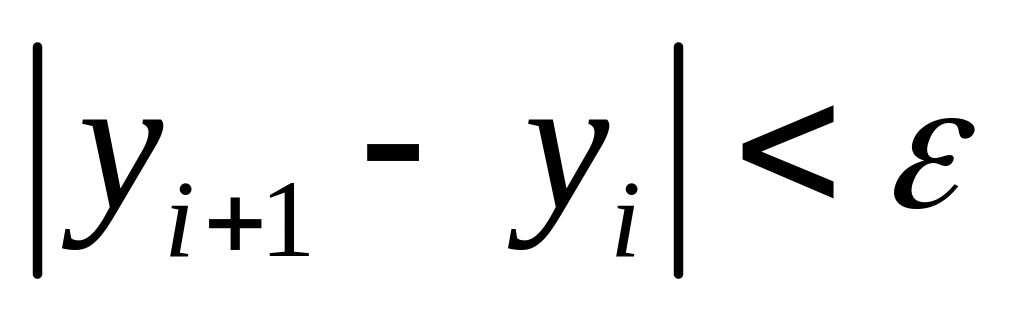7. Проверить полученное решение командой solve.

Практическое задание 3

Найти решение нелинейной системы методом Ньютона

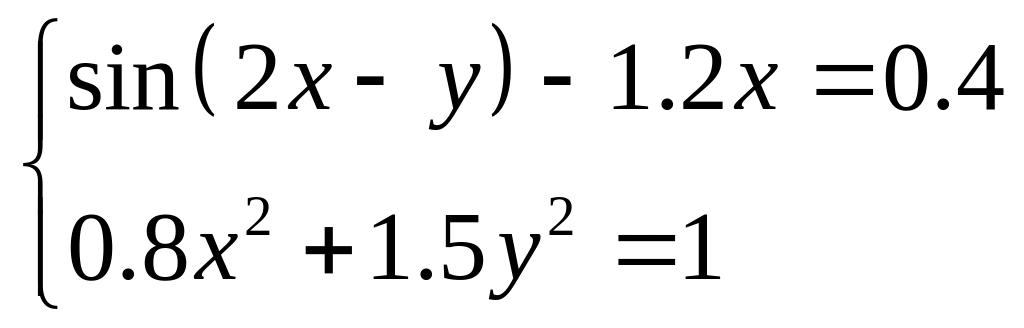
План решения:

1. Записать два уравнения так, чтобы в правой части был ноль, обозначить F, а из второго обозначить G (через ).

2. Построить графики этих функций, используя функцию implicitplot пакета plots

3. Выбрать начальное приближение и из графика, обозначить x[0] и y[0]

4. Задать погрешность вычислений

5. Найти частные производные 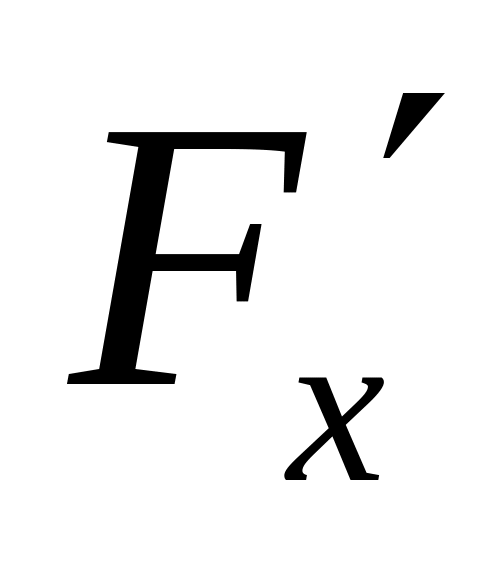, , 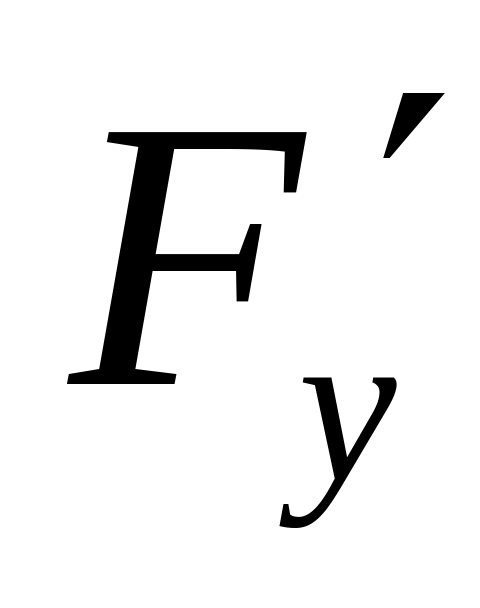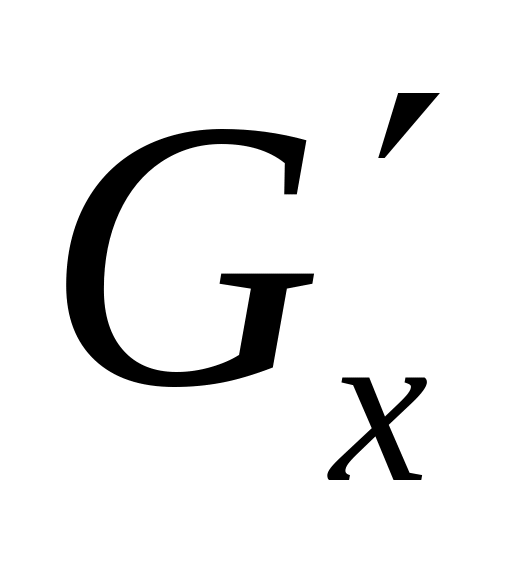и 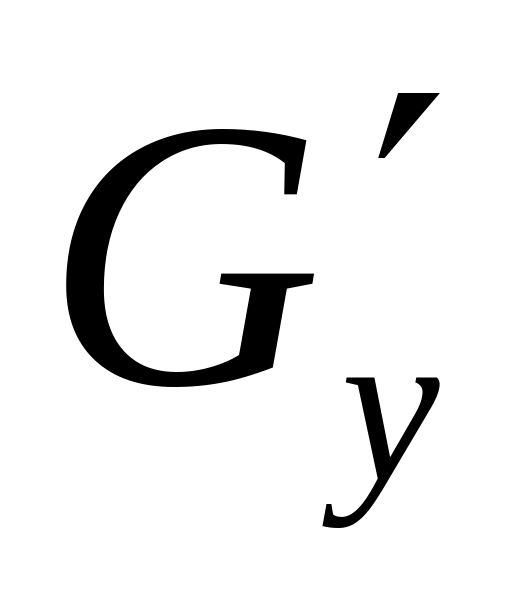и сделать их функциями своих аргументов, для этого можно использовать команду unapply(функция, от_чего_зависит)

6. Найти решение путем итераций по формуле где: , Все эти формулы пишутся в цикле, выход из которого осуществляется когда и . Определители находятся с помощью функции Determinant пакета LinearAlgebra.

7. Проверить полученное решение командой solve.

Занятие 8. Решение дифференциальных уравнений

В общем случае уравнение имеет бесконечное множество решений.

Задача Коши

Решением задачи Коши

с

на интервале является такая дифференцируемая функция , которая удовлетворяет условиям

и для всех .

Кривая, соответствующая решению данной задачи должна проходить через начальную точку .

Если известно общее решение уравнения , то задача Коши решается достаточно просто. Она заключается в нахождении частного решения, удовлетворяющего условия , которое легда определяется из общего решения подстановкой в него значения и определения произвольной постоянной при условии, что значение функции в точке должно быть равно .

Метод Эйлера

Однако, не все задачи Коши имеют явное решение.

Первый подход называется методом Эйлера и годится для иллюстрации понятий, включенных в методы повышенной точности. Он имеет ограниченное применение из-за большой ошибки накапливаемой в процессе вычислений.

Пусть ‑ интервал, на котором требуется найти решение корректно поставленной задачи Коши с . Вместо нахождения функции, удовлетворяющей данным условиям, сгененрируем семейство точек и используем их для приближения. Сначала разобьем интервал на одинаковых подынтервалов и выберем точки

для , где .

Значение называется длиной шага.

Метод Эйлера заключается в нахождении точек, которые приближают кривую , по формулам:

для