Практическое задание 2.

Решить уравнение методом деления пополам.

Для данного метода функция должна быть задана в виде , что мы и имеем.

План:

1. Задать фукнцию 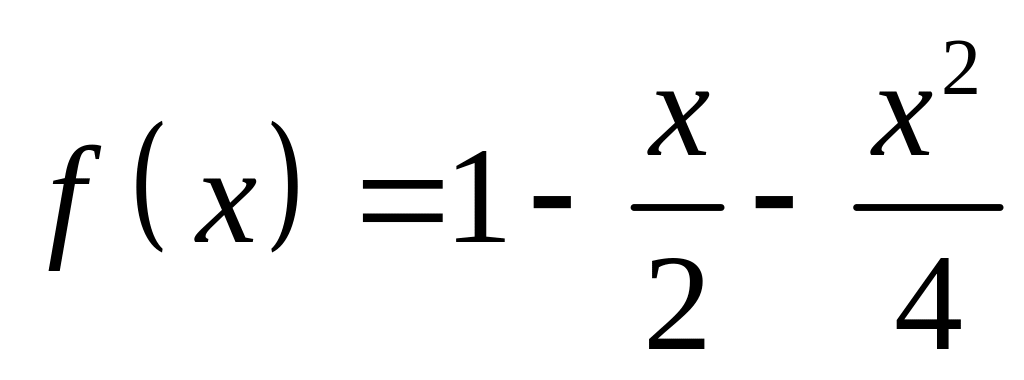через оператор и обозначить ее f

2. Построить график функции f(x)

3. Задать концы интервалов как переменные a, b (исходя из графика так, чтобы )

4. Задать точность вычисления epsilon:=0.0001;

5. Реализовать алгоритм нахождения корня. Для этого необходимо написать цикл по переменной от 1 до 10000 (любое большое число на случай зацикливания) с условием while ((b-a)>epsilon) (условие пишется в той же строчке, что и for). Внутри цикла считаетя середина интервала 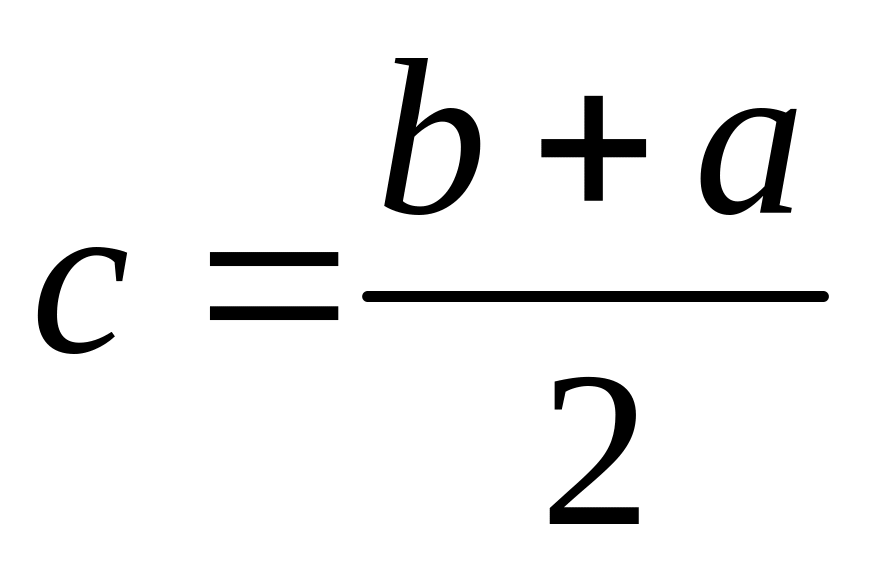и проверяется два условия: 1) если ; 2) . Если выполняетя 1), то b:=c; если 2), то a:=c;

6. Найти точное решение уравнения, используя solve.

Практическое задание 3.

Решить уравнение методом Ньютона.

Функция задана в нужном .

План:

1. Задать фукнцию через оператор и обозначить ее f

2. Построить график функции f(x)

3. Задать концы интервалов как переменные a, b (исходя из графика)

4. Задать точность вычисления epsilon:=0.0001;

5. Взять за начальное приближение левый конец интервала, т.е. x[0]:=a;

6. Реализовать алгоритм нахождения корня по формуле , Для этого необходимо написать цикл по переменной от 0 до 10000 (любое большое число на случай зацикливания) с условием выхода при выполнении условия 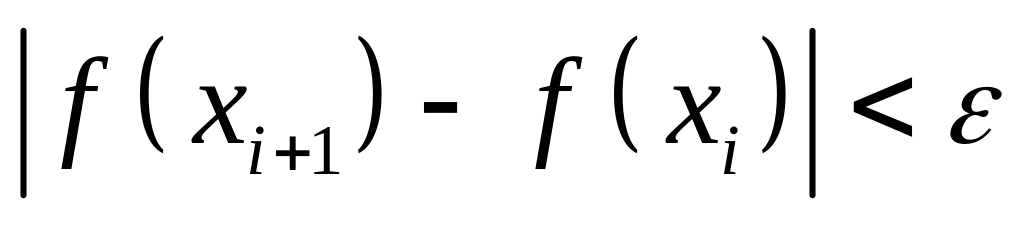(условие выхода через оператор if ‑ проверка условия и break ‑ выход). Для нахождения значения производной в точке можно использовать следующую команду D(f)(x[i])

7. Найти точное решение уравнения, используя solve.

Практическое задание 4.

Реализовать любой из выше перечисленных методов в виде процедуры.

Например, для метода итераций:

iteracii:=рrос([ список_формальных_параметров ])

[ local список_локальных_переменных; ]

[ global список_глобальных_переменных; ]

последовательность_операторов

end proc

В список_формальных_параметров будут входить g, a, epsilon.

Они задаются вне процедуры, и ее вызов будет выглядеть следующим образом:

iteracii(g,a,epsilon);

список_локальных_переменных – это список вспомогательных переменных, которые используются внутри процедуры, в данном методе это i, x.

Глобальных переменных нет.

Занятие 7. Решение систем Линейные системы. Метод Гаусса

Рассмотрим данный метод на примере системы, состоящей из 3 линейных уравнений:

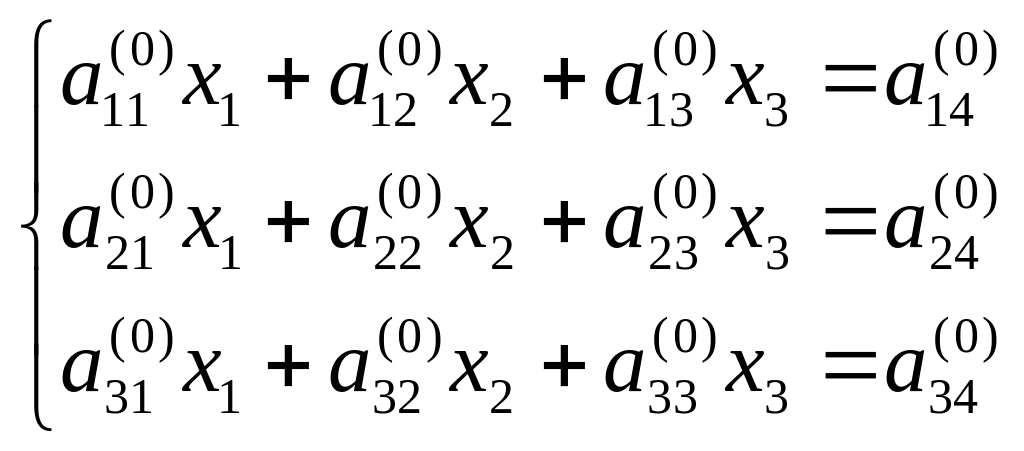(1)

Предположим, что коэффициент , называемый ведущим элементов не равен 0.

Разделим первое уравнение на , получим

(2)

где

Исключаем неизвестную из оставшихся уравнений, это делается вычитанием уравнения (2), умноженного на коэффициент при переменной в соответствующем уравнении:

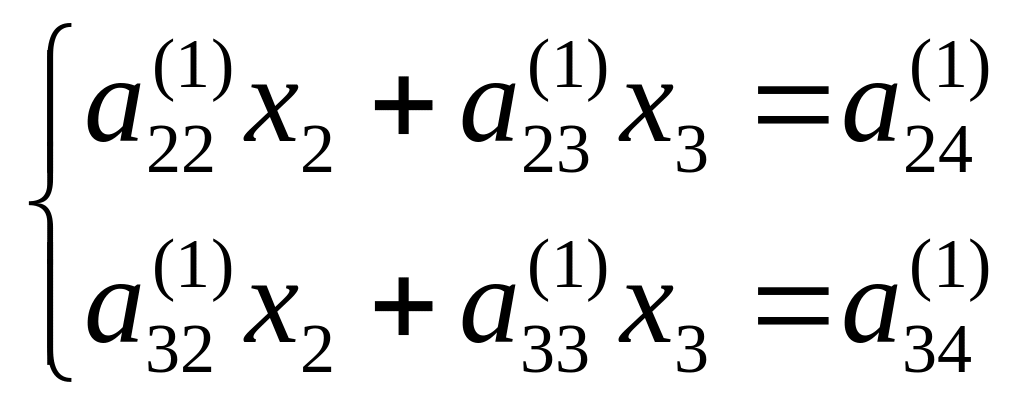(3)

где

Допустим, что ведущий элемент отличен от нуля. Тогда разделив на него первое уравнение получим:

где

Исключив из полученного уравнения получим:

где

Наконец, если , то разделив на него получим

где

Итак, система эквивалентна следующей системе:

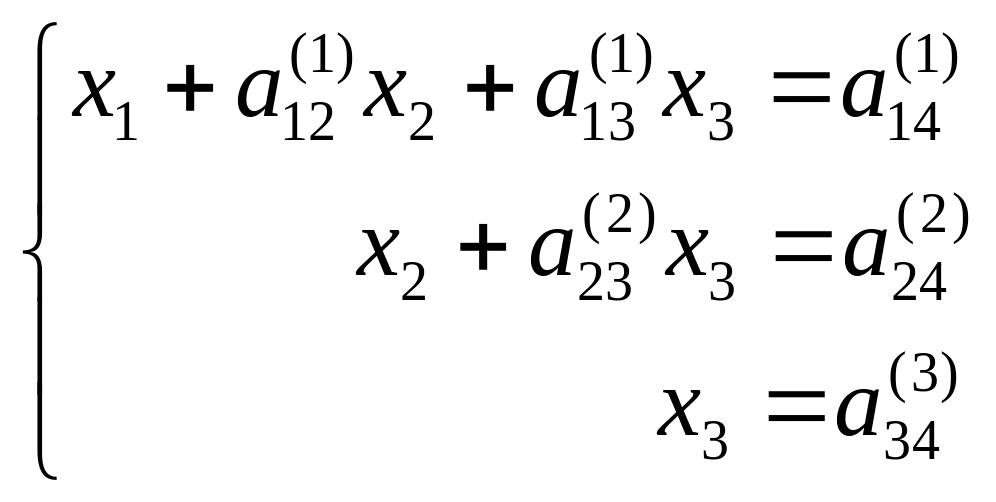
Из нее неизвестные находятся в обратном порядке.

Решение системы с помощью обратной матрицы

Пусть дана система в матричном виде

где

‑ матрица коэффициентов

‑ вектор неизвестных

‑ вектор правой части

Тогда

Метод простой итерации

Пусть дана система

представим ее в виде

Метод простой итерации состоит в следующем: выбирается произвольный вектор и строится итерационная последовательность по формуле

,

Решение нелинейных систем

Метод итераций

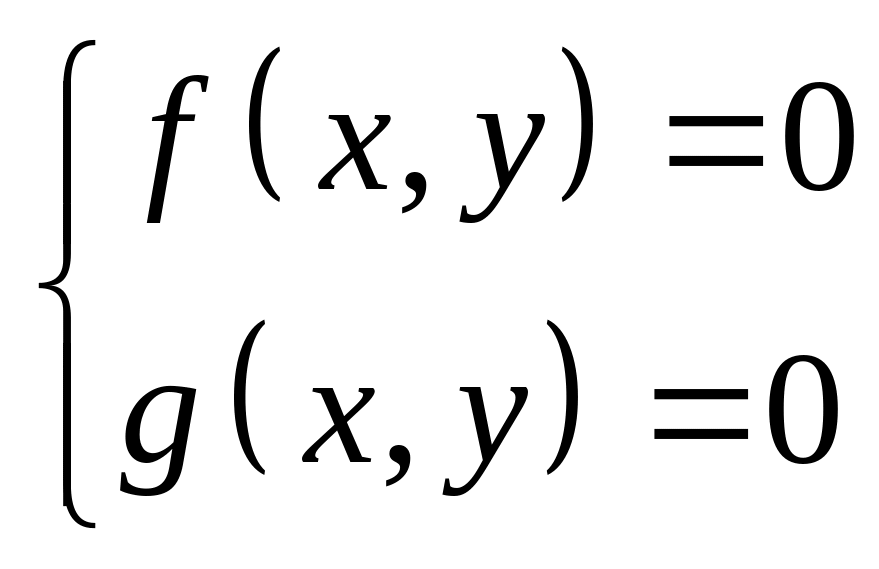
Перепишем систему в виде:

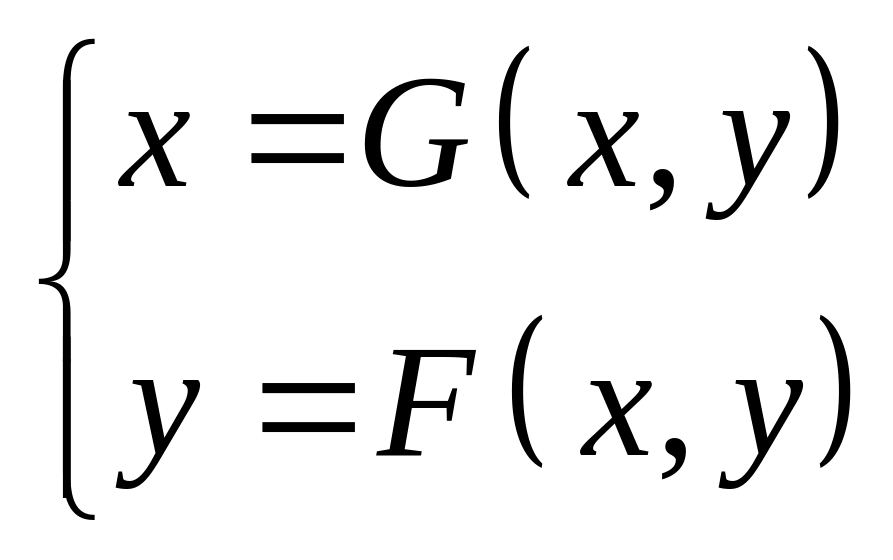
Выбирается начальное приближение из области (область с единственным решением).

Для того, чтобы данный метод был применим для уточнения решения системы необходимо выполение условий в области :

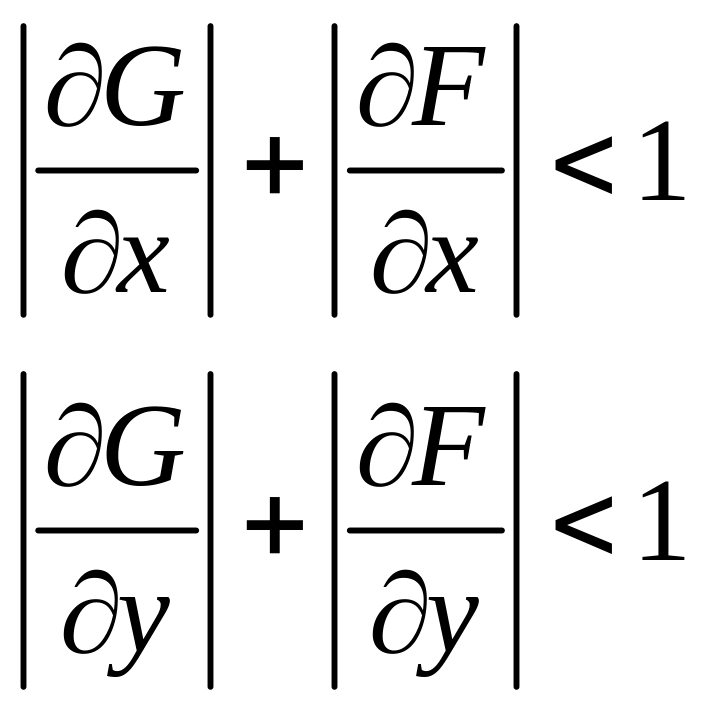
Вычисления производим по формулам:

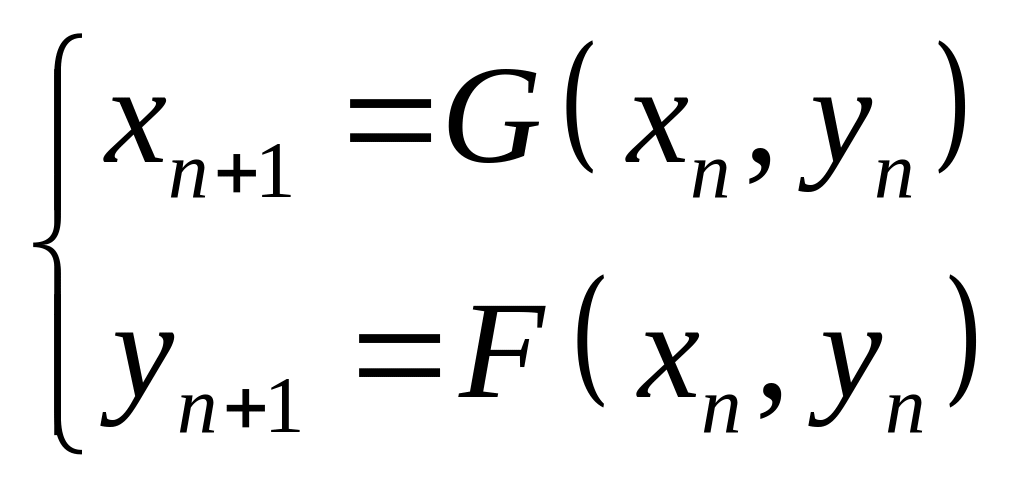
Метод Ньютона.

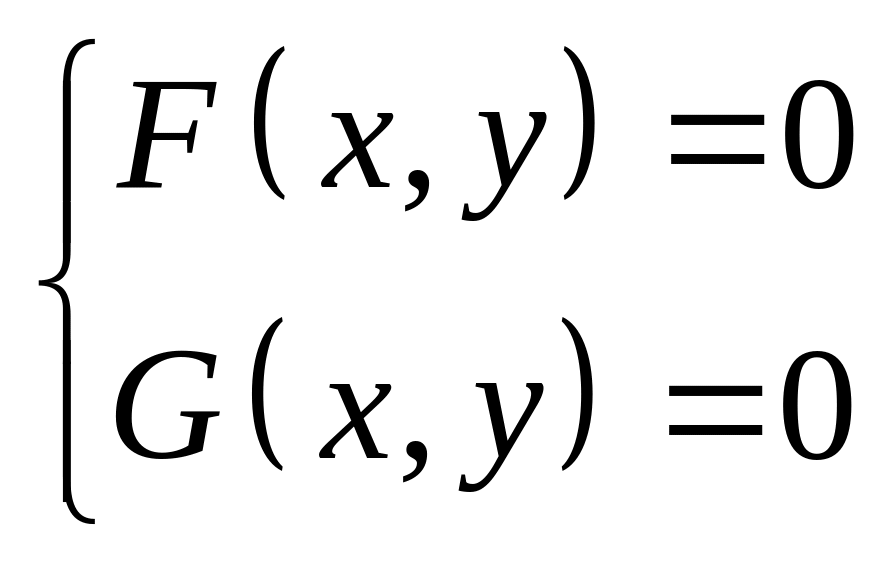
Выбирается начальное приближение из области (область с единственным решением).

Найдем частные производные:

Уточнение корней производим методом Ньютона:

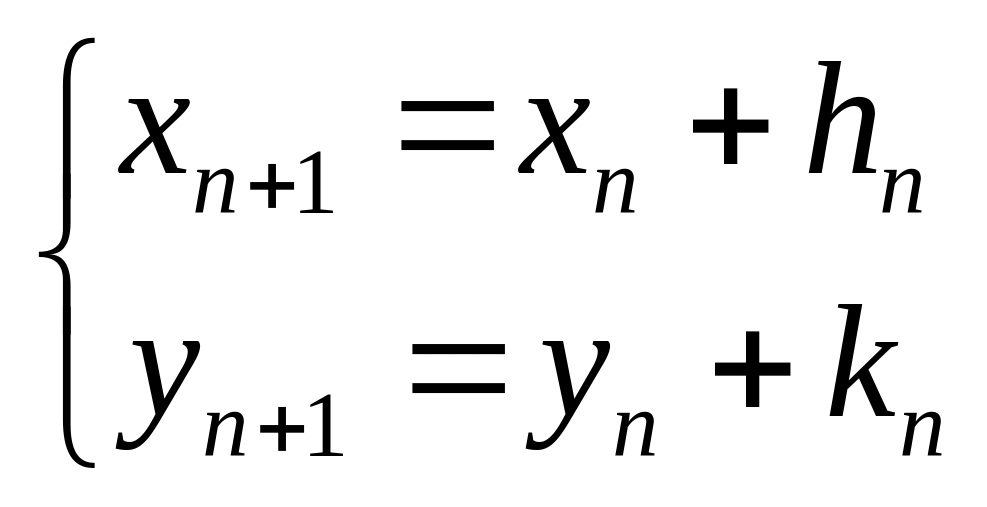
Где

,

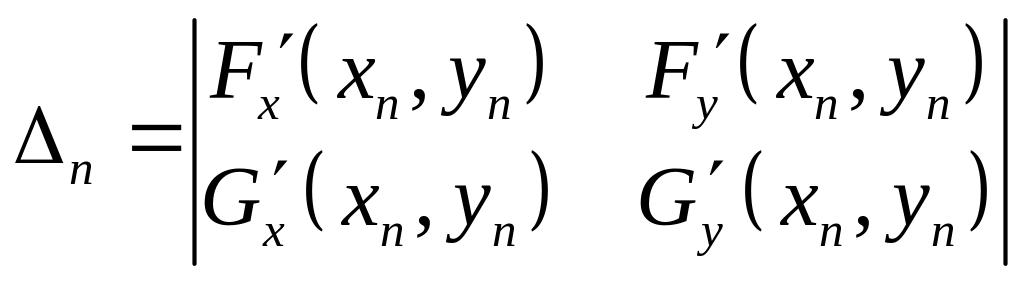
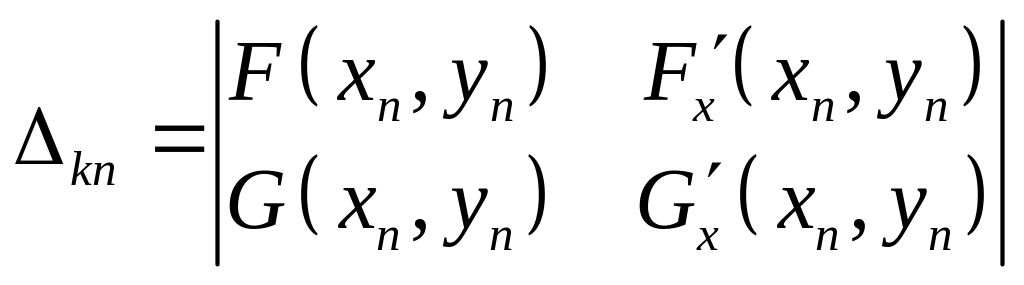
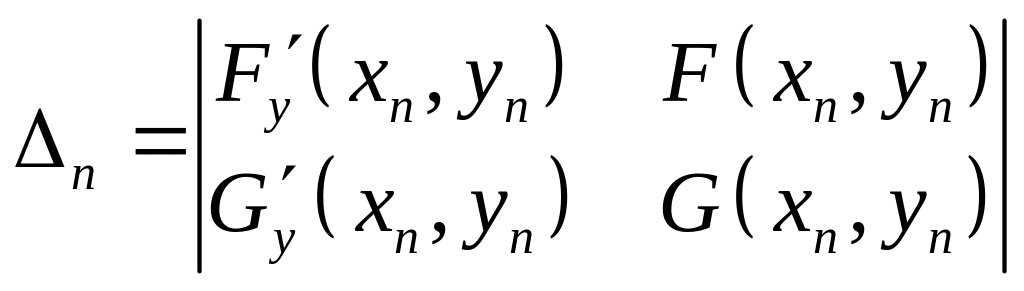
Линейная алгебра

В Maple выполнение преобразований линейной алгебры можно осуществлять с помощью команд двух пакетов: linaig и LinearAlgebra, функциональность которых практически одинакова. Первый пакет входил в состав и всех предыдущих версий Maple, тогда как второй пакет — это новое средство, позволяющее работать с числовыми матрицами, в том числе и с матрицами больших размеров, используя всю мощь известного пакета численных расчетов NAG (Numerical Algorithms Group).

Основными объектами, с которыми работают команды этих пакетов, являются матрицы, однако матрицы одного пакета не эквивалентны матрицам другого.