Метод Ньютона

Данный метод называетя также методом касательных

Метод Ньютона сходится к корню быстрее, чем метод деления пополам и метод итераций.

Рассмотрим уравнение

Метод Ньютона заключается в нахождении корня уравнения по итерационной формуле

для (3)

Остановка итераций происходит, когда .

Процедуры в Maple

В языках программирования процедуры позволяют выделить код в одну связанную единицу с тем, чтобы в дальнейшем простым обращением к ее имени инициировать выполнение всех, содержащихся в ней операторов. Обычно процедуры используются для реализации некоторых часто выполняемых действий.

Определение процедуры Maple имеет следующий общий синтаксис:

рrос([ список_формальных_параметров ])

[ local список__локальных_переменных; ]

[ global список_глобальных_переменных; ]

последовательность_операторов

end proc

При объявлении процедуры единственным обязательным параметром является последовательность операторов, формирующих тело процедуры. Остальные параметры, определяющие локальные и глобальные переменные, список формальных параметров, задающие специальные опции режима выполнения процедуры и строку описания, могут полностью отсутствовать.

Определение процедуры на рабочем листе создает объект Maple, которому, однако, следует дать имя, чтобы в дальнейшем можно было обращаться к нему. Это осуществляется обычной операцией присваивания:

> vector_length:=proc(x,y) sqrt(x^2+y^2); end proc;

После того, как процедура определена и ей присвоено имя, ее можно вызвать и выполнить с помощью оператора вызова функции, в котором задается имя процедуры, а в скобках определяются фактические переменные, которые заменяют в теле процедуры все формальные параметры:

> vector_length(2,5);

Обычно возвращаемым значением процедуры является значение последнего вычисленного в теле процедуры оператора. В нашем примере последний, и единственный, оператор вычисляет квадратный корень из суммы квадратов параметров процедуры.

Если необходимо вернуть из процедуры не последний оператор, то необходимо пользоваться командой return.

Процедуру можно написать используя специальную нотацию:

> vector_length:=(x,y)->sqrt(x^2+y^2);

> vector_length(2,5);

Практическое задание 1.

Решить уравнение методом итераций.

Для метода итераций функция должна быть задана в виде , а мы имеем . Для преобразования функции к нужному виду прибавим к обеим частям равенства, получим:

т.е.

План:

1. Задать фукнцию через оператор и обозначить ее g

2. Построить график функции g(x)-x

3. Задать концы интервалов как переменные a, b (исходя из графика)

4. Задать точность вычисления epsilon:=0.0001;

5. Взять за начальное приближение левый конец интервала, т.е. x[0]:=a;

6. Реализовать алгоритм нахождения корня по формуле , Для этого необходимо написать цикл по переменной 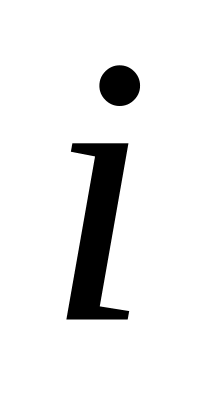от 0 до 10000 (любое большое число на случай зацикливания) с условием выхода при выполнении условия (условие выхода через оператор if ‑ проверка условия и break ‑ выход).

7. Найти точное решение уравнения, используя solve.