Методичка. Расчет на прочность при сложном нагружении

Здесь α=f (h/b), h/b=2, α=0,246.

τВ = γτmax = 0,795 • 40,6 = 32,3 МПа,

здесь γ = f(h/b), h/b= 2, γ = 0,795.

σэквА III = 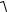σ2A + 4τ2A = 452 + 4 • 32,32 = 78,7 МПа.

4. ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ

Приемы определения напряжений и деформаций, которые использовались при решении частных задач сложного сопротивления (косой изгиб, внецентренное растяжение-сжатие, изгиб с кручением), могут быть распространены на более сложные случаи нагружения, когда в поперечных сечениях бруса действуют все шесть силовых факторов.

В качестве примера рассмотрим расчет ломаного бруса, показанного на рис. 4.1.

Пример 6. Для заданного ломаного бруса (рис. 4.1), имеющего круглые поперечные сечения в пределах элементов длиной l1 и l2, прямоугольное сечение в пределах элемента длиной l3, требуется выполнить следующие расчеты:

1.Построить эпюры продольных усилий, изгибающих и крутящих моментов.

2.Определить допускаемые нагрузки Р и q, исходя из заданных размеров прямоугольного сечения элемента бруса длиной l3.

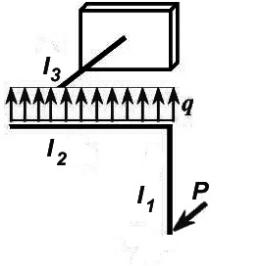
3. Определить диаметры круглых сечений элементов бруса длиной l1 и l2.

Рис. 5.1

Примечания:

а) построение эпюр внутренних силовых факторов производить, используя скользящую систему координат с постоянным направлением осей; б) в расчетах на прочность использовать теорию максимальных

касательных напряжений; в) прямоугольное сечение бруса длиной /3 считать ориентирован-

ным так, что плоскость наибольшей жесткости совпадает с плоскостью действия максимального изгибающего момента.

Таблица исходных значений

Решение.

1. Построение эпюр внутренних силовых факторов.

Для определения величины и характера распределения внутренних силовых факторов по длине каждого участка ломаного бру-

са построим эпюры продольных сил N, изгибающих Мизг и крутящих Мкр моментов.

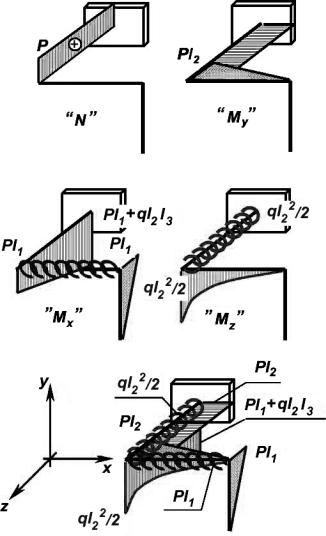
Поперечными силами Q в расчетах, как правило, пренебрегают, так как их влияние незначительно. Для ломаного бруса, показанного на рис. 4.1, эпюры внутренних силовых факторов приведены на рис. 4.2.

Рис. 4.2

2. Определение допускаемой нагрузки Р и q

2.1. Определение опасного сечения элемента бруса длиной l3. Анализ эпюр показывает, что наиболее опасным является сечение в заделке. В этом сечении действуют: максимальный из-

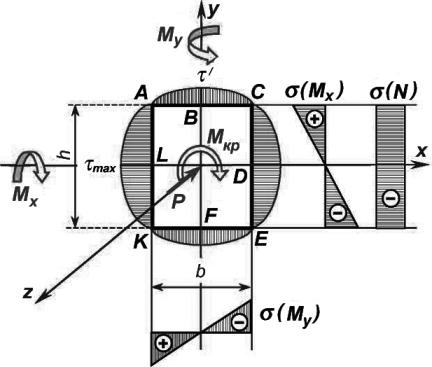
гибающий момент Мх, изгибающий момент М , постоянный по длине участка, крутящий момент Mz, а также продольная сжимающая сила N.

2.2. Определение опасных точек в опасном сечении элемента Прямоугольное сечение элемента бруса длиной l3 ориенти-

руем так, чтобы плоскость наибольшей жесткости совпадала с плоскостью действия максимального изгибающего момента Мх. Положение плоскости наибольшей жесткости определяется жесткостью поперечного сечения относительно главных центральных осей х и у, в частности, величиной максимального момента сопротивления. В данном случае (рис. 4.3)

Максимальный изгибающий момент также действует относительно оси х (Мх>Му). Следовательно, сечение должно быть расположено так, как показано на рис. 4.3.

Рис. 4.3

Для определения положения опасных точек в опасном сечении построим эпюры распределения нормальных (от N, Mx, Мy ) и касательных (от Мкр= Мz) напряжений (рис. 4.3).

Эпюры нормальных и касательных напряжений показывают, что наиболее опасными являются следующие три точки этого сечения:

точка E, где суммируются нормальные напряжения от N, Mx, My ,касательные напряжения равны нулю,

точка D, где суммируются нормальные напряжения от N, My, a касательные напряжения от Мкр принимают максимальные значения,

точка F, где суммируются нормальные напряжения от N, Мх, а касательные напряжения равны τ1.

2.3.Определение величин изгибающих и крутящих моментов

вопасном сечении и моментов сопротивления.

Выразим q через величину Р. Так как по условию задачи

Моменты в опасном сечении имеют следующие значения:

Mx = Pl1 + ql2l3 = P 0.23 + 4,64 • P 0,28 • 0,33 = 0,659 • P, My = Pl2 = 0.28 • P,

При заданном соотношении h/b = 2,5 и b=3 см моменты сопротивления принимают следующие значения:

w x = bh2 = 3 • 7,52 = 28,13 см3, 6 6

w кр = αhb2 = 0,256 • 7,5 • 32 = 17,3 см3,

где при h/b=2,5 α=0,256.

2.4 Определение допускаемой нагрузки Расчет в точке Е. В точке Е имеют место только нормальные

напряжения, поэтому на основании принципа независимости действия сил

Так как в точке D имеют место нормальные и касательные напряжения, используем условие прочности по III гипотезе

σэквIII = σ2 + 4τ2 ЎЬσ

свободного конца бруса, где действует один силовой фактор - изгибающий момент М х = Р11. Условие прочности будет иметь вид

d1=36 мм.

3.2. Определение диаметра круглого сечения элемента бруса длиной /2

Анализ эпюр (рис. 4.2) на втором участке показывает, что опасным является сечение в конце участка, если двигаться со свободного конца бруса, где изгибающие моменты Му и Мх принимают максимальные значения, а крутящий момент Мz= Р1z, т.е. имеет место изгиб с кручением бруса круглого поперечного сечения (см. гл 3.1). На рис. 4.4 два изгибающих момента приведены к одному суммарному и показаны опасные точки сечения А и В.

Рис.4.4

Величины моментов

My = Pl2 = 3305 • 0.28 = 925.4 Нм,

Мz = q • l22 = 15344 • 0,282 = 601,5 Нм, 2 2

Мх=Мкр=Рl1=3305·0,23=760,2 Нм.

Условие прочности для круглого сечения согласно III теории прочности имеет вид

d2=44 мм.

Литература

1.Сопротивление материалов. Под ред. А.Ф. Смирнова. - М.: Высшая школа, 1975.

2.Цвей А.Ю. Лекции по сопротивлению материалов с примерами расчетов. ч.1 – М.: МАДИ, 1997.

3.Рубинин М.В. Руководство к практическим занятиям по сопротивлению материалов. М.:РОСВУЗИЗДАТ, 1963.

Оглавление Введение……………………………………………………………. 3

1.Косой изгиб…………………………………………………………. 3

1.1.Определение напряжений при косом изгибе…………………. 3

1.2.Определение положения нейтральной линии при косом из-

гибе…………………………………………………………………... 6

1.3.Определение перемещений при косом изгибе……………….. 9

2.Внецентренное растяжение (сжатие)………………………….. 13

2.1.Определение напряжений при внецентренном растяжении

(сжатии)……………………………………………………………… 14

2.2.Определение положения нейтральной линии………………… 16

2.3.Понятие о ядре сечения…………………………………………… 18 3. Совместное действие изгиба и кручения……………………….. 22

3.1.Расчет брусьев круглого поперечного сечения……………….. 23

3.2.Расчет брусьев прямоугольного сечения………………………. 27

4.Общий случай сложного сопротивления……………………….. 31

Литература…………………………………………………………… 39

Редактор Н.П. Лапина Технический редактор Е.К. Евстратова