
Методичка. Расчет на прочность при сложном нагружении
.pdfМОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Кафедра строительной механики
Утверждаю Зав. кафедрой профессор
________И.В. Демьянушко
« 30 » января 2007г.
А.М. ВАХРОМЕЕВ
РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАГРУЖЕНИИ
Методические указания
МОСКВА 2007
УДК 624.046 ББК 34.41
© Московский автомобильно-дорожный институт (государственный технический университет), 2007
2 |
- - |
Введение
Под сложным нагружением подразумевают различные комбинации простейших деформаций бруса - растяжения или сжатия, сдвига, кручения и изгиба. При этом, на основании принципа независимости действия сил, напряжения и деформации в стержне при сложном нагружении определяют суммированием напряжений или деформаций, вызванных каждым внутренним силовым фактором в отдельности. Напомним, что этот принцип применим в тех случаях, когда имеют место только упругие деформации, а материал подчиняется закону Гука.
Рассмотрение вопросов, связанных с расчетом на прочность и жесткость элементов, работающих в условиях сложного нагружения, начнем с частных случаев, которые наиболее популярны.
1. КОСОЙ ИЗГИБ
Изгиб, при котором внешние нагрузки действуют в плоскости, не совпадающей ни с одной из главных плоскостей инерции, называется косым изгибом (рис.1.1). Главной плоскостью инерции называется такая плоскость, которая включает в себя ось балки (z) и одну из главных центральных осей инерции поперечного сечения (x или у). Плоскость, в которой располагаются внешние нагрузки, называется силовой плоскостью.
1.1. Определение напряжений при косом изгибе
Рассмотрим консольную балку, нагруженную сосредоточенной силой, как показано на рис.1.2.
Находим проекции силы Р на главные центральные оси инерции x и y (см. рис.1.2):
Px = P sin α и Рy = P cos α.
Каждая из проекций располагается в одной из главных центральных плоскостей инерции и, таким образом, косой изгиб
3 |
- - |
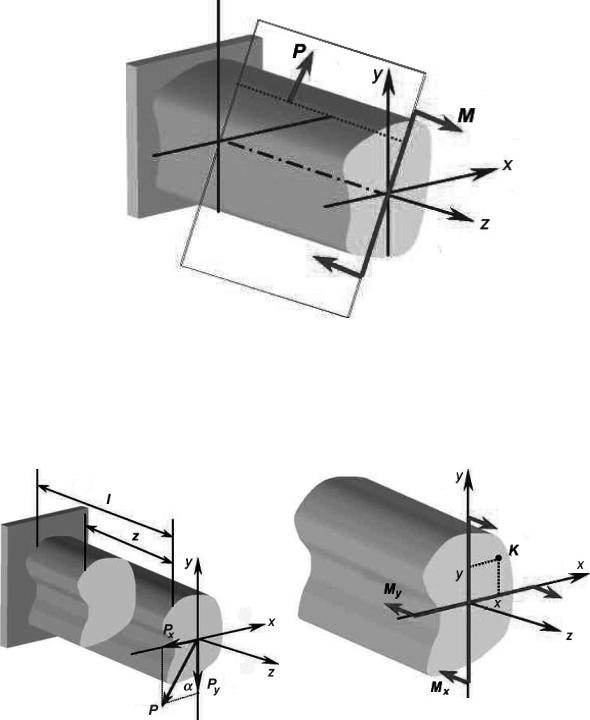
Силовая плоскость
Рис. 1.1
является сочетанием двух плоских поперечных изгибов и часто называется двойным.
Рис. 1.2
В произвольном сечении на расстоянии z от точки приложения силы имеют место четыре внутренних силовых фактора:
поперечные силы Qx=Px=Psinα,
Qy=Py= P cos α;
4 |
- - |
и изгибающие моменты М y = Px y = P y sin α,
Mx= Py = P x cos α.
Определим напряжения, возникающие в произвольной точке К рассматриваемого сечения (см. рис.1.2): от изгибающего момента
Мx
σ/ = M х y ,
J x
от изгибающего момента My
σ// = M y х ,
J y
здесь x и у - координаты точки, в которой рассчитывают напряжения.
Знак напряжения зависит от характера деформации (растяже- ние-плюс, сжатие-минус). В нашем случае оба напряжения являются растягивающими и имеют знак плюс.
На основании ПНДС полное нормальное напряжение в точке К равно их алгебраической сумме
σ |
= σ/ + σ// = M x y + M y x . |
(1.1) |
|
|
J x |
J y |
|
При проведении расчетов на прочность условие прочности составляется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений. Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.
В связи с этим большое значение приобретают вопросы, связанные с определением положения нейтральной линии.
5 |
- - |
1.2. Определение положения нейтральной линии при косом изгибе
Положение нейтральной линии можно определить с помощью формулы (1.1), если предположить, что точка К с координатами x0, y0 лежит на нейтральной линии. В этом случае нормальное напряжение в точке равно нулю
M x |
|
M y |
|
|
σ = J x |
y 0 + J y x0 |
= 0 |
, |
|
Pz cos α y 0 |
+ Pz sinα x0 = 0 |
|||
J x |
|
J y |
|
|
или |
|
|
|
|
cos α y 0 |
+ sinα x0 = 0 . |
(1.2) |
||
J x |
|
J y |
|
|
Уравнение нейтральной линии при косом изгибе (1.2) есть уравнение прямой, проходящей через начало координат.
Положение нейтральной линии определяется тангенсом угла ее наклона β (рис.1.3) к главной оси x. С учетом (1.2) находим
y 0 |
= sinα |
J x = tgα |
J x , |
|
|||
x0 |
|
||||||
|
cos α |
J y |
J y |
|
|
||
tgβ = |
|
y 0 |
, tgβ = tgα |
J x |
. |
(1.3) |
|
|
x0 |
J y |
|||||
|
|
|
|
|
|
||
Так как в общем случае Jx ≠ Jy и, следовательно, |tg β| ≠|tg α|, то можно заключить, что при косом изгибе нейтральная линия не перпендикулярна к линии действия внешней силы.
Из формулы (1.3) следует, что для сечений с Jx=Jy (квадрат, круг, кольцо, правильный многоугольник), т.е. для сечений, у которых любые центральные оси являются главными, углы α и β равны, и нейтральная линия перпендикулярна линии действия
6 |
- - |

внешней силы. Балки такого сечения не испытывают деформации косого изгиба.
Определение положения нейтральной линии позволяет выявить опасные точки сечения. Для этого следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными (точки A и B на рис.1.3).
Силоваялиния |
Нейтральная линия |
Рис. 1.3
Для некоторых сечений (прямоугольник, двутавр, швеллер и т.п.) наиболее напряженные точки расположены в углах этих сечений, т.е. их можно найти без определения положения нейтральной линии (рис.1.4).
Условия прочности составляют в зависимости от свойств того материала, из которого изготовлен элемент конструкции (брус).
7 |
- - |
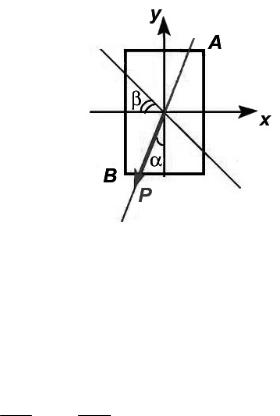
Рис. 1.4
Для хрупкого материала используют два условия прочности - для опасной точки, где имеет место растяжение (для нашего случая т. А на рис.1.3), и для точки, где имеет место сжатие
(т. В)
σmaxp = MJ x y A + MJ y xA ЎЬ[σp],
xy
c |
= |
M x |
y |
|
+ |
M y |
xВ |
ЎЬ[ |
]. |
(1.4) |
|
|
J y |
||||||||
σmax |
|
J x |
В |
|
σс |
|
|
|||
Необходимость использования двух условий прочности для хрупкого материала объясняется разными механическими свойствами материала при растяжении и сжатии. Хрупкий материал плохо сопротивляется растяжению и хорошо - сжатию.
Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, используют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения
|σmax |= |
M x y |
+ M y x ЎЬ[σ ], |
(1.5) |
|
J x |
J y |
|
где x и у - координаты данной точки.
При расчетах на прочность касательными напряжениями от поперечных сил пренебрегают, т.к. их влияние незначительно.
8 |
- - |
1.3. Определение перемещений при косом изгибе
Перемещения при косом изгибе определяют по принципу независимости действия сил, т.е. рассчитывают прогибы x и у в направлении главных осей, а величину полного прогиба в любом сечении балки получают геометрическим суммированием:
= |
2x + |
2y . |
Например, для балки, изображенной на рис.1.2, прогиб конца консоли определится следующим образом:
|
Py l 3 |
P cos α |
l 3 , |
||||
y = |
|
|
|
= |
3EJx |
|
|
|
|
|
|
||||
|
3EJx |
|
|
||||
|
P l 3 |
P sinα |
|
|
|||
x = |
x |
|
= |
3EJy |
l 3 , |
||
|
|
||||||
|
3EJy |
|
|
||||
= |
|
2x + |
2y . |
|
|
||
Рис. 1.5
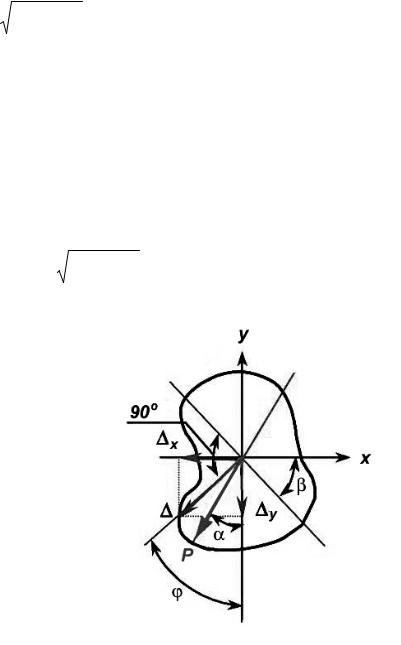
Направление полного перемещения tgφ определится величиной отношения x / у (рис.1.5)
9 |
- - |

tgφ = |
x |
= |
P sin α3EJx |
= |
Jx |
tgα . |
(1.6) |
|
y |
3EJy P cos α |
Jy |
||||||
|
|
|
|
|
Сравнивая выражения (1.6) и (1.3), видим, что tgφ = tgβ, т.е. направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы
(рис.1.5.).
Рассмотрим примеры расчета балок на косой изгиб.
Пример 1. Подобрать прямоугольное сечение балки (рис.1.6) при условии, что h = 2b, [σ]=160МПа, Р=60кН, α=30°, l=2,8м.
Рис. 1.6
Решение. Разложив силу Р на две составляющие, действующие по направлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов Mx и Мy (рис.1.7). Наибольшие моменты действуют в среднем сечении, где
Mzmax = |
Pl |
cos α , |
M ymax = |
Pl |
sinα , |
4 |
4 |
следовательно, это сечение является опасным.
Для определения положения опасной точки расставим знаки от σ(Mx) и σ(Му) в угловых точках поперечного сечения балки (рис.1.7).При действии момента Mx в точках А и D будут иметь место положительные (растягивающие) напряжения, а в точках С
10 |
- - |
