Методичка. Расчет на прочность при сложном нагружении

удален малый прямоугольник с размерами hxt (фигура II). За исходную ось примем ось z.

В этом случае в поперечном сечении АВ возникает два внутренних силовых фактора: продольная сила N - Р и изгибающий момент Мх - Рус.

С целью определения опасной точки расставим знаки напряжений по боковым сторонам поперечного сечения (рис. 2.6). От продольной силы во всех точках сечения имеют место положительные (растягивающие) напряжения. От изгибающего момента слева от оси хс имеют место растягивающие напряжения (знак плюс), справа - сжимающие (знак минус).

Таким образом, максимальные нормальные напряжения возникают в т. А

где FH - площадь ослабленного сечения, равная FI – FII =7 см2;

Jхс - момент инерции ослабленного сечения относительно главной центральной оси хс

yA - расстояние от нейтральной линии хс до наиболее удаленной точки (т. А)

y A = h2 + yC = 5,643 см.

В результате максимальные нормальные напряжения будут равны

3. СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ

На практике деформации кручения часто сопутствует изгиб. Например, совместное действие изгиба с кручением приходится учитывать при расчете валов машин, испытывающих воздействие окружных и радиальных усилий. Сочетание изгиба с кручением имеет место в пространственных рамах, коленчатых валах и других элементах конструкций.

В предыдущих главах рассматривались такие частные случаи сложного сопротивления (косой изгиб, внецентренное растяжение или сжатие), при которых в поперечных сечениях бруса возникали только нормальные напряжения, и, следовательно, имело место одноосное напряженное состояние. Это позволило при выводе расчетных формул использовать сечения произвольной формы.

В случае изгиба с кручением от крутящего момента в поперечных сечениях бруса возникают касательные напряжения, которые рассчитываются по-разному для круглых и прямоугольных брусьев. Вследствие этого рассматривать расчет сечений произвольной формы не представляется возможным.

3.1. Расчет брусьев круглого поперечного сечения

Пусть в поперечном сечении круглого бруса (рис. 3.1) действуют два изгибающих момента Mx и Мy , которые могут быть приведены к одному суммарному моменту MΣ, так как все центральные оси круга являются главными

Максимального значения нормальные напряжения от Mx достигают в т.А (положительные а), или в т. В (отрицательные а). Знаки напряжений устанавливают по характеру деформаций.

Кроме того, в поперечном сечении бруса имеет место крутящий момент (Мкр=Мz) (рис. 3.1). Максимального значения касательные напряжения от Мкр достигают в точках на контуре сечения. Следовательно, т. А (или т. В) является опасной, для которой и составляется условие прочности.

Рис. 3.1

В т. А имеют место напряжения

Проанализируем напряжения в т.А. С этой целью вырежем в окрестностях этой точки элементарный параллелепипед, передняя грань которого совпадает с поперечным сечением бруса

(рис. 3.2).

Рис. 3.2

Как видно из рис. 3.2, в данном случае имеет место плоское напряженное состояние и расчет на прочность должен

проводиться по одной из гипотез прочности. Для пластичных материалов применяют гипотезу наибольших касательных напряжений (III) или энергетическую гипотезу (IV).

Условие прочности по III гипотезе записывается в виде

тезе прочности.

Условие прочности по IV гипотезе прочности записывается в виде

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к III гипотезе, а для очень хрупких - к I гипотезе

Аналогичный расчет проводится и для кольцевого сечения.

Пример 4. Стальной вал круглого поперечного сечения передает мощность N=14.7 кВт при угловой скорости ω=10,5 рад/с. Величина наибольшего изгибающего момента, действующего на вал, Ми=1,5 кНм. Исходя из условий прочности по III и IV гипотезам прочности, определить необходимый диаметр вала, если [σ] =80 МПа.

Решение. Условие прочности при одновременном действии изгиба и кручения по III гипотезе прочности

Находим величину передаваемого валом крутящего момента

Эквивалентный момент по III гипотезе прочности равен

МэквIII = Ми2 + М2кр = 15002 +14002 = 2050 Нм,

адиаметрвала

или dIII=63,5 мм.

Условие прочности при одновременном действии изгиба и кручения по IV гипотезе прочности

dIV=62,3 мм.

Таким образом, в результате расчета по энергетической теории прочности получается более экономичный размер сечения, чем исходя из критерия наибольших касательных напряжений.

3.2 Расчет брусьев прямоугольного сечения

Рассмотрим брус прямоугольного сечения, нагруженный таким образом, что в его поперечных сечениях действуют изгибающие моменты Мх и Mv, a также крутящий момент Мz (рис. 3.3).

Рис. 3.3

Чтобы проверить прочность бруса, нужно в опасном сечении найти опасную точку, вычислить для нее эквивалентное на-

пряжение (по одной из теорий прочности) и сопоставить его с допускаемым напряжением.

Для нахождения опасной точки сечения построим эпюры напряжений от всех силовых факторов (рис. 3.4).

Рис.3.4

Эпюры нормальных и касательных напряжений наглядно показывают, что в отличие от круглого сечения, точки, в которых имеют место максимальные нормальные и максимальные касательные напряжения, не совпадают. Вследствие этого условие прочности составляют, как минимум, для трех наиболее опасных точек поперечного сечения.

Опасной точкой по нормальным напряжениям является

отрицательны. Касательные напряжения от крутящего момента в этих точках равны нулю. Таким образом, в этих точках имеет место линейное напряженное состояние.

Опасной точкой по касательным напряжениям является точка N (или L), лежащая в середине длинной стороны прямоугольника. Кроме того, в этой точке действуют максимальные нормальные напряжения от изгибающего момента Му.

Следует отметить, что в точке М (или К), расположенной в середине короткой стороны прямоугольного сечения также действуют касательные напряжения (несколько меньшие τтах) и максимальные нормальные напряжения от Mx.

Таким образом, в точках поперечного сечения N, М (L,K) имеет место плоское напряженное состояние, которое обуславливает использование гипотез прочности при расчетах на прочность. Для пластичных материалов применяют III (наибольших касательных напряжений) и IV (энергетическую) гипотезы прочности.

Составим условия прочности для трех предположительно опасных точек поперечного сечения

σэквIII = σ2 + 4τ2 = 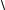σN2 + 4τmax2 ЎЬσ

σэквIII = 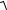σ2 + 4τ2 = 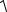σM2 + 4(τ/)2 ЎЬσ

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к III гипотезе, а для очень хрупких - к I гипотезе

Пример 5. Коленчатый стальной стержень прямоугольного поперечного сечения защемлен одним концом и нагружен поперечной силой Р=0.9 кН на свободном конце. Определить в точках А и В защемленного сечения расчетные напряжения по III теории прочности (рис. 3.5).

Решение. Построим эпюру моментов с целью определения величин внутренних силовых факторов, действующих в поперечном сечении стержня в заделке (рис. 3.6).

В результате действия силы Р в защемленном сечении будут действовать изгибающий и крутящий моменты

Mx=Mи= 0.9 • 0.9 = 0.81 кНм, Mz = Мкр = 0.9 • 0.6 = 0.54 кНм.

Эквивалентные напряжения по III гипотезе прочности рассчитываются по формуле