
- •1)Предмет теории вероятности. Её роль в экономической теории.
- •2 Подхода исследования случ. Явлений:
- •2) Основные понятия тв. Объективная и субъективная стороны вер-ти.
- •3) Частота события, её сходимость по вероятности.
- •4. Классич. Опр-е «р». Осн. Формулы комбинаторики.
- •5. Геом. Опр-е «р». Достоинства и огр-я.
- •6. Прост. И слож. С-я. Сумма соб-ий. Т.Сложения «р».
- •7. Прост. И слож соб-я. Произвед-е с-ий. Услов. «р» с-я. Т. Умн-я «р».
- •8. Ф. Бернулли. Ф. Пуассона. Сфера их применения.
- •9. Лок. И интегр. Теоремы Муавра-Лапласа.
- •10. Формула полной вер-ти. Ф. Байеса.
- •20. "Точные" зр. Распределение Гаусса. Понятие о квантилях распределения.
- •21. "Точные" зр. Распределение Пирсона(хи квадрат).
- •22. "Точные" зр. Распределение Стьюдента.
- •23. "Точные" зр. Распределение Фишера.
- •24. Понятие многомерной дискретной случайной величины и закон ее распределения.
- •25. Функция распределения многомерной св.
- •26. Понятие многомерной непрерывной св. Плотность вероятности двумерной св.
- •27. Условные зр. Числовые характеристик двумерной св.
- •28. Закон больших чисел. Неравенство Маркова.
- •29. Закон больших чисел. Неравенство Чебышева.
- •30. Закон больших чисел. Теорема Чебышева
- •31. Закон больших чисел. Т. Бернулли. Т. Пуассона
- •32. Закон больших чисел. Центральная предельная теорема
- •Корреляционный момент и коэффициент корреляции
- •34. Понятие о регрессионной зависимости св. Линей. Ур-я регрессии
- •35. Осн. Понятия математ. Статистики
- •Вариационные Ряды
- •37. Эмпирическая функция распределения.
- •38. Числовые характеристики вариационного ряда.
- •39. Точечная оценка параметров распределения. Свойства.
- •40. Метод максимального правдоподобия получения точечной оценки.
- •41. Метод наименьших квадратов получения точечной оценки.
- •42. Метод моментов получения точечной оценки.
- •43. Понятие о доверительных оценках и доверительном интервале.
- •46. Доверительная оценка неизвестного Mx при неизвестной Dx
- •47. Доверительная оценка неизвестной Dx при неизвестном Mx.
- •48.Элементы общей теории проверки статистических гипотез
- •49.Статисическая проверка гипотез:проблема выбора критической области. Ошибки 1 и 2 рода.
- •50.Статистическая проверка гипотез :сравнение математических ожиданий 2 генеральных совокупностей при известных σ2х , и σ2у
- •55. Статистическая проверка гипотез: непараметрический критерий сравнения Уилкоксона.
- •57. Статистическая проверка гипотез: критерий согласия (Пирсона).
- •59. Статистическая проверка гипотез о равенстве вероятности события заданному числовому значению.
28. Закон больших чисел. Неравенство Маркова.
ЗБЧ - это некоторый принцип, согласно которому совокупные действия большого числа СВ приводят к результату почти независящему от случая. Другими словами, при большом числе СВ их ср.знач. перестает быть случайным т.е его можно предсказать с опр. степенью доверия. В узком понимании это ряд теорем, в каждой из кот. для тех или иных условий устанавливается факт приближения ср.характеристик большого числа испытаний к некоторым постоянным величинам.
Неравенство Маркова.
Теорема. Если СВ
Х принимает только неотрицательные
значения и имеет матем.ожидание
![]() ,
то для любого положительного числа А
выполняется неравенство:
,
то для любого положительного числа А
выполняется неравенство:
![]() ,
,
![]()
Неравенство Маркова
применимо к любым неотрицательным
случайным величинам. Оно не дает
эффективного результата в случае, когда
![]() .
Док-во: Х=(x1,x2…xn)
P(X=xi)=pi;
i=
.
Док-во: Х=(x1,x2…xn)
P(X=xi)=pi;
i=![]() . A>0
. A>0
Выберем, что ![]() i=
i=
![]()
Заменив возможное значение хk+1, xk+2…xnна А>0 в послед. неравенстве, то получаем более строгое неравенство, т.е.
![]()
![]()
![]()
![]()
29. Закон больших чисел. Неравенство Чебышева.
ЗБЧ - это некоторый принцип, согласно которому совокупные действия большого числа СВ приводят к результату почти независящему от случая. Другими словами, при большом числе СВ их ср.знач. перестает быть случайным т.е его можно предсказать с опр. степенью доверия. В узком понимании это ряд теорем, в каждой из кот. для тех или иных условий устанавливается факт приближения ср.характеристик большого числа испытаний к некоторым постоянным величинам.
Неравенство Чебышева.
Теорема. Для любой
СВ, имеющей матем.ожидание и дисперсию,
справедливо неравенство Чебышева:
![]() .
.
Вторая форма
записи:
![]()
Следствие 1.
Для СВ Х, распределенной по биномиальному
ЗР(Х-число экспериментов в схеме из n
независимых испытаний, в которых событие
А наступило) справедливо неравенство:
![]() ,где
npg=D(X),
np=M(X)
,где
npg=D(X),
np=M(X)
Следствие 2.
(для нахождения доли): Для частоты
события, распределнного по нормированному
биномиальному закону, справедливо
неравенство:
![]() ,где
pg/n=D(X),
p=M(X).
,где
pg/n=D(X),
p=M(X).
Док-во: Применив нер-во Маркова к С.В. X’=(X - Mx)2; А=ℰ2
![]()
![]()
1)![]() ;
;
![]()
2)![]()
И следует:
![]()
Теорема Чебышева:
Если дисперсия n
независимых СВ Х1, Х2,...,Хn
ограничены одной и той же постоянной
(D(x)=C),
то при
![]() их
ср.арифм. сходится по вероятности
ср.арифм. их математического ожидания.
их
ср.арифм. сходится по вероятности
ср.арифм. их математического ожидания.
![]()
Следствие. Если
дисперсия n
независимых СВ ограничена одной и той
же постоянной С, а их математические
ожидания совпадают
![]() ,
то ср.арифм. исходных СВ сходится по
вероятности мат.ожидания отдельной СВ.
,
то ср.арифм. исходных СВ сходится по
вероятности мат.ожидания отдельной СВ.
![]()
30. Закон больших чисел. Теорема Чебышева
ЗБЧ - это некоторый принцип, согласно которому совокупные действия большого числа СВ приводят к результату почти независящему от случая. Другими словами, при большом числе СВ их ср.знач. перестает быть случайным т.е его можно предсказать с опр. степенью доверия. В узком понимании это ряд теорем, в каждой из кот. для тех или иных условий устанавливается факт приближения ср.характеристик большого числа испытаний к некоторым постоянным величинам.
Теорема Чебышева: Если дисперсия n независимых СВ Х1,Х2....Хn ограничены одной и той же постоянной (D(xi)≤C), то при их ср.арифм. сходится по вероятности к ср.арифм. их математического ожидания т.е не имеет четких границ области распределения.
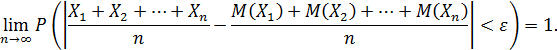
Док-во: X1,
X2…
Xn–
независ. С.В. M(xi)=aii=
D(xi)![]() C
C
Рассмотрим С.В.![]() для
кот. запишем нерав-во Чебышева:
для
кот. запишем нерав-во Чебышева:
![]()
![]()
![]() Тогда:
Тогда:
![]()
Следствие. Если дисперсия n независимых СВ ограничена одной и той же постоянной С, а их математические ожидания совпадают , то ср.арифм. исходных СВ сходится по вероятности мат.ожидания отдельной СВ.
