10. Формула полной вер-ти. Ф. Байеса.

H_1,H_2, …,H_n-события, образующие полную группу событий (гипотезы). Нек-ое соб-е А может наступить совместно с одной из гипотез H_1,H_{2, …},H_n, A=A* H₁+A* H₂+…+A* H_n

P(A)=P(A* H₁)+P(A* H₂)+…+P(A* H_n)=P(H₁)*P(A/ H₁)+P(H₂)* P(A/ H₂)+…+P(A/ H_n)

- Ф-ла полной вер-ти. Выделим i-ое слагаемое из правой части формулы полной вер-ти отсюда выразим - ф-ла Байеса. По ф-ле Байеса осущ-ся переоценка вероятностей гипотез при условии, что соб-е А наступило.

Вер-ти при Hi по наз-ют априорными P(Hi), i=1,n; , - апостериорные.

11. Дискретные случайные величины. Формы задания их законов распределения.

СВ- некоторая функция, определенная на множестве элементарных исходов.

Дискретная СВ -СВ, возможные значения кот. изолированы друг от друга и образуют конечное или бесконечное, но всегда счетное множество.

ЗР- всякое соотношение, устанавливающее связь м/у возможными значениями СВ и соответствующими им вероятностями.

ЗР ДСВ м.б. задан на основе ряда распределения и функции распределения. Ряд распределения – таблица, сост. из 2-х строк, первая из кот. указ. возможные знач. СВ, во второй- соответствующие им вероятности.

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

=P(X= ), i=1,2,…

События x= , x= образуют полную группу событий.

Основное свойство ряда распределения: =1

Графическое распределение ряда распределения называют многоугольником распределения.

Функция распр. СВ Х – вероятность того, что СВ Х принимает значения меньшее текущей величины Х. F(x)=P(X˂x)

Св-ва: 1. F(x)- неубывающая функция.

2. F(-∞)=0

3. F(+∞)=1

График функции распределения ДСВ является ступенчатым. Величина i-го скачка графиков функции распр. ДСВ = вероятности того, что P(X= ). Функция распр. называют интегральным законом распр. СВ. Функция распр. непрерывна слева.

Типовые ЗР ДСВ:

Биномиальный ЗР с возможными значениями 0,1,2,…,n

ДСВ имеет биномиальный ЗР, если вероятности ее возможных значений определяются по формуле P(X=m)=

Параметрами распределения являются n и p. Область применения- схема независимых испытаний. ДСВ с возможными значениями 0, ,…,1 имеет нормированное биномиальное распределение если вероятности возможных ее знач. опред. по формуле

P(X= )=

M(X)=np; D(X)=npq; σ(X)= .Если по нормированному биномиальному ЗР(P(X=m/n)), то M(X)=p; D(X)=pq/n;

ДСВ с возможными значениями 0,1,2,…,m распр. по закону Пуассона с параметром λ=np, если вероятности ее значений опред. по формуле: P(X=m)= * .Числовые характеристики: М(Х)= λ, D(X)= λ

12. Непрерывные случайные величины. Формы задания их законов распределения.

СВ, ЗР которой может быть задан на основе непрерывной функции распр-я назыв. непрерывной.Или Непрерывная СВ-СВ,возможные значения которых заполняют некоторый интервал числовой оси.

ЗР НСВ может быть задан:

1)на основе непрерывной функции распределения;

2) плотности распределения ее вероятностей;

Плотностью распре. НСВ f(x) называется ее функция распределения.

f(x)= , F(x)=P(X˂x)

Св-ва:1.f(x)≥0, xϵR, f(x)- неубыв. функция и F ́(x)≥0

2. f(-∞)=f(+∞)=0

3. (площадь под кривой=1)

P(a˂x˂b)=F(b)-F(a)=

13. Числовые характеристики дискретных СВ. Свойства математического ожидания.

Мат.ожидание-это число равное сумме произведений возможных значений CB X на соответствующие им вероятности.

, x_i=возможные значения CВ p_i=P(X= x_i)

Мат. Ожидание характеризует средневзвешанную оценку возможных значений CВ Х. Физический смысл мат.ожидания-это центр тяжести возможных значений СВ.

Св-ва мат. ожидания:

1.М(с)=с, с-const 2. M(с*X)=с*M(x), с-const 3.M(X±Y)=M(X)±M(Y) 4. M(X±C)=M(X)±(C), c-const 5.M(X*Y)=M(X)*M(Y); Х,Y-независимые СВ. 6. M[X-M(X)]=0 ,7. M(X*Y)=M(X)*M(Y)+ -зависимые СВ

Доказательство 1св-о. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С.

Дисперсией CB X наз. мат.ожидание квадрата отклонения CB X от ее мат.ожидания

D(x)=M((X-M_x)²)= M(X^2)- M^2 (X)

Дисперсия характеризует степень рассеяния возможных значений CВ Х относительно ее мат.ожидания.

Среднее квадратическое отклонение CB X- это корень квадратный из ее дисперсии

Медианой CB X называют ее возможное значение, делящее ее закон расп-я на равные части.

=0,5

Модой CB X называют ее возможное значение с наибольшей вероятностью.

14. Числовые характеристики непрерывных СВ. Метод моментов. Свойства дисперсии.

СВ, ЗР которой может быть задан на основе непрерывной функции распределения, называется непрерывной.

Среднее значение (математическое ожидание, первый начальный момент) непрерывной СВ вычисляется по формуле . Дисперсия или второй центральный момент имеет вид . Свойства дисперсии:

1)D(C)=0; C-const 2) D(kX)=k^2D(X); k-const3) D(X±Y)=D(X)+D(Y), где X и Y– независимые СВ 4) D(X±C)= D(X), C-const ,5) D(X)=M(X^2)- M^2 (X), 6) D(X+Y)=D(X)+D(Y)+ -зависимые СВ

Доказ-о: = M(X^2)- M^2 (X)

Величина – среднеквадратическое (стандартное) отклонение случайной величины от среднего значения. Медианой называется значение , для которого выполняется соотношение

Модой СВ Х называется ее наиболее вероятное значение.

Начальный момент первого порядка называется математическим ожиданием(+/-) СВ: = , где - возможные значения СВ.х – текущая величина. - плотность распределения. =p(x= )

Центральный момент второго порядка называется дисперсией СВ(+): D(x)= . Дисперсия характеризует степень рассеянности Х относительно М(Х). Центральный момент 3-го порядка– для исследования ассиметрии. = , где – центральный момент 3-го порядка – ср.кв.окл- характеризует крутость графика плотности распределения СВ.

ЦМ 4-го порядка– для оценки коэффициента эксцесса. Коэффициент эксцесса определяется по формуле = ,,-характеризует островершинность или плосковершинности ЗР СВ.

15. Равномерный ЗР СВ. Сфера проявления.

Непрерывная СВ распределена по равномерному ЗР с параметрами a и b, если плотность вероятности распределения задается формулой: f(x)=

Теорема. Функция распределения равномерна распределенной СВ на интервале от a до b задается формулой:

f(x)=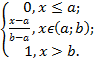

Мат. ожидание СВ опред. по формуле M(x)= ;

Дисперсия: D(x)= ; σ(x)= ;

Доказ-во: F(x)=

xϵ(a; b]; F(x)= *x = ;

xϵ(b; +∞); F(x)= *x = *(b-a)=1.

Сфера проявления.

1) Случайное число, полученное на основе генератора случайных чисел, является случайной величиной с равномерным законом распределения с параметрами по умолчанию a=0, b=1.

2) Время ожидания транспорта (метр)– случайная величина с равномерным законом распределения, параметр которого a=0, b= , – интервал движения транспорта.

3) Угол остановки юлы–случайная величина с равномерным законом распределения, где a=0, b=2π(360 гр).

16. Показательный ЗР СВ. Сфера проявления.

Непрерывная СВ X распределена по показательному закону с параметром λ, если плотность вероятности ее распределения задается формулой.

f(x)=

Функция распределения СВ, распределенной по показательному ЗР задается формулой

F(x)= , Док-во: x

x dx=λ*(-1/λ)* =-( -1)=1- .

M(x) = , D(x) = , = .

Доказ-во:D(x)=M( )- (x)= – .

Сфера проявления.

1. Время обслуживания заявки в сфере массового обслуживания с простейшим потоком событий;2.Остаток времени обслуживания заявки имеет тот же закон распределения(с тем же параметром), что и начало обслуживания заявки, вне зависимости от того, как долго длилось это обслуживание.

17. Нормальный ЗР СВ. Сфера проявления. Правило «трех сигм»

Непрерывная СВ распределена по нормальному ЗР с параметрами и , если плотность распределения задается формулой: f(x)= * , - параметры распределения, кот. являются числовыми характеристиками нормального ЗР СВ.

Теорема: Функция распределения нормального ЗР СВ задается формулой:f (x)= * dx.

Св-ва: 1. P(a -Ф( )

2. P(|X- ); где Ф(х)- функция Лапласа.

Правило «трех сигм»: Если СВ Х имеет норм. ЗР, то выполняется равенство:P(X- )=0,9973 (1)

Справедливо и обратное утверждение.

Если для СВ Х вып. равенство (1), то СВ имеет нормальный ЗР.P(|x-

Частным случаем Норм. ЗР является распределение Гаусса, плотность распр. при этом задается формулой: f(x)= * ; =0, =1. Распределение Гаусса так же назыв. стандартным нормальным ЗР. Переход от нормального ЗР к распределению Гаусса осуществляется по формулам: T= , где Х-СВ с норм. ЗР, Т-СВ имеющая распр-е Гаусса.

Сфера проявления НЗР: расчеты по определению вероятности попадания СВ в пределы задаваемых интервалов ее возможных значений. НЗР подчинено подавляющее большинство ошибок(ошибки измерения величин, ошибки определения местонахождения объектов, ошибки стрельбы и др.).

18. Биномиальный ЗР. Сфера проявления.

Биномиальный ЗР с возможными значениями 0,1,2,…,n

ДСВ имеет биномиальный ЗР, если вероятности ее возможных значений определяются по формуле P(X=m)=

Параметрами распределения являются n и p. Область применения- схема независимых испытаний. Числовые хар-ки: M(X)=np; D(X)=npq; σ(X)= . ДСВ с возможными значениями 0, ,…,1 имеет нормированное биномиальное распределение если вероятности возможных ее знач. опред. по формуле

P(X= )= . Числов. хар-ки: M(X)=p; D(X)=pq/n;

Биномиальный ЗР широко применяется в теории и практике стат. контроля качества продукции, при описании функционирования систем массового облуживания, при моделировании цен активов, в теории стрельбы и в других областях.

19. Распределения Пуассона. Сфера применения.

ДСВ с возможными значениями 0,1,2,…,m распр. по закону Пуассона с параметром λ=np, если вероятности ее значений опред. по формуле: P(X=m)= = (λ).

Матем. ожидание и дисперсия СВ: M(X)=λ, D(X)=λ.

Доказ-во: СВ X: a=M(X)= = = =λ = λ (1+λ+ +…)= λ =λ.

Распределение Пуассона имеет место в схеме независимых испытаний при n->∞, p->0,n*p-> λ(const) ,применяется в сфере массового обслуживания с простейшим потоком событий(число заявок на орп. интервале времени).По закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание, поступивших в единицу времени в системах массового обслуживания.