
- •1)Предмет теории вероятности. Её роль в экономической теории.
- •2 Подхода исследования случ. Явлений:
- •2) Основные понятия тв. Объективная и субъективная стороны вер-ти.
- •3) Частота события, её сходимость по вероятности.
- •4. Классич. Опр-е «р». Осн. Формулы комбинаторики.
- •5. Геом. Опр-е «р». Достоинства и огр-я.
- •6. Прост. И слож. С-я. Сумма соб-ий. Т.Сложения «р».
- •7. Прост. И слож соб-я. Произвед-е с-ий. Услов. «р» с-я. Т. Умн-я «р».
- •8. Ф. Бернулли. Ф. Пуассона. Сфера их применения.
- •9. Лок. И интегр. Теоремы Муавра-Лапласа.
- •10. Формула полной вер-ти. Ф. Байеса.
- •20. "Точные" зр. Распределение Гаусса. Понятие о квантилях распределения.
- •21. "Точные" зр. Распределение Пирсона(хи квадрат).
- •22. "Точные" зр. Распределение Стьюдента.
- •23. "Точные" зр. Распределение Фишера.
- •24. Понятие многомерной дискретной случайной величины и закон ее распределения.
- •25. Функция распределения многомерной св.
- •26. Понятие многомерной непрерывной св. Плотность вероятности двумерной св.
- •27. Условные зр. Числовые характеристик двумерной св.
- •28. Закон больших чисел. Неравенство Маркова.
- •29. Закон больших чисел. Неравенство Чебышева.
- •30. Закон больших чисел. Теорема Чебышева
- •31. Закон больших чисел. Т. Бернулли. Т. Пуассона
- •32. Закон больших чисел. Центральная предельная теорема
- •Корреляционный момент и коэффициент корреляции
- •34. Понятие о регрессионной зависимости св. Линей. Ур-я регрессии
- •35. Осн. Понятия математ. Статистики
- •Вариационные Ряды
- •37. Эмпирическая функция распределения.
- •38. Числовые характеристики вариационного ряда.
- •39. Точечная оценка параметров распределения. Свойства.
- •40. Метод максимального правдоподобия получения точечной оценки.
- •41. Метод наименьших квадратов получения точечной оценки.
- •42. Метод моментов получения точечной оценки.
- •43. Понятие о доверительных оценках и доверительном интервале.
- •46. Доверительная оценка неизвестного Mx при неизвестной Dx
- •47. Доверительная оценка неизвестной Dx при неизвестном Mx.
- •48.Элементы общей теории проверки статистических гипотез
- •49.Статисическая проверка гипотез:проблема выбора критической области. Ошибки 1 и 2 рода.
- •50.Статистическая проверка гипотез :сравнение математических ожиданий 2 генеральных совокупностей при известных σ2х , и σ2у
- •55. Статистическая проверка гипотез: непараметрический критерий сравнения Уилкоксона.
- •57. Статистическая проверка гипотез: критерий согласия (Пирсона).
- •59. Статистическая проверка гипотез о равенстве вероятности события заданному числовому значению.
8. Ф. Бернулли. Ф. Пуассона. Сфера их применения.
Если некот. соб-е А наступает с одной и той же вер-ю в каж. из n испытаний, причем вер-ть наступления соб-я А в каж. испытании не зависит от исходов др. испытаний, то такие испытания наз-ют независимыми относ-но соб-я А. Такая послед-ть соб-ий получила название схемы Бернулли или схемы независимых испытаний.
Т.
Бернулли:
Если вер-ть р наступления соб-я А в каж.
испытании постоянна, то вер-ть Рm,n
того, что соб-е А наступит m
раз в n
независ. испытаниях =:
![]() - ф-ла Бернулли
(если общее число испытаний не большое).
Док-во:
пусть n=3,
m=2.
В – соб-е А наступит 2 раза в 3х независ.
испытаниях; В1 – соб-е А наступит в 1ом
испытании, В2 –во 2ом и В3 – в 3ем.
- ф-ла Бернулли
(если общее число испытаний не большое).
Док-во:
пусть n=3,
m=2.
В – соб-е А наступит 2 раза в 3х независ.
испытаниях; В1 – соб-е А наступит в 1ом
испытании, В2 –во 2ом и В3 – в 3ем.
![]() -несовместные соб-я.
-несовместные соб-я.
![]() рр(1-р)+р(1-р)р+(1-р)рр=
рр(1-р)+р(1-р)р+(1-р)рр=
![]() ч.т.д.
ч.т.д.
Т.
Пуассона:
Если вер-ть р наступления соб-я А в
отдельном испытании постоянна и
![]() при неограниченном возрастании числа
проводимых испытаний
,
причем
при неограниченном возрастании числа
проводимых испытаний
,
причем
![]() ,
где
,
где
![]() ,
то вер-ть того, что соб-е А наступит m
раз в n
независ. испытаниях приближенно равна:
,
то вер-ть того, что соб-е А наступит m
раз в n
независ. испытаниях приближенно равна:
![]() -ф-ла Пуассона
(применяется при
-ф-ла Пуассона
(применяется при
![]() ).
Док-во:
т.к. имеет место схема независ. исп-ий,
то вер-ть того, что
).
Док-во:
т.к. имеет место схема независ. исп-ий,
то вер-ть того, что
![]()
![]()
![]() [
[![]() ]
]![]()
![]() переходя к пределу при
,
получаем
переходя к пределу при
,
получаем
 по 2му замеч. пределу ч.т.д.
по 2му замеч. пределу ч.т.д.
Примеры повторных испытаний: 1) многократное извлечение из урны 1 шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну; 2) повторение одним стрелком выстрелов по 1 и той же мишени при условии, что вер-ть удачного попадания при каж. выстреле принимается одинаковой.3)сфера массового обслуживания с простейшим потоком событий(число заявок на опр. интервале времени).Свойства: стационарность, ординарность, отсутствие последействия.
9. Лок. И интегр. Теоремы Муавра-Лапласа.
Локк.
теорема:
Если вер-ть р наступления соб-я А в каж.
испытании постоянна и отлична от 0 и 1,
то вер-ть Pm,n
того, что соб-я А наступит m
раз в n
независ. испытаниях при достаточно
больших n
приближенно равна:
![]() ,
где
,
где
![]() ,
x=
,
x=![]()
Условия:
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
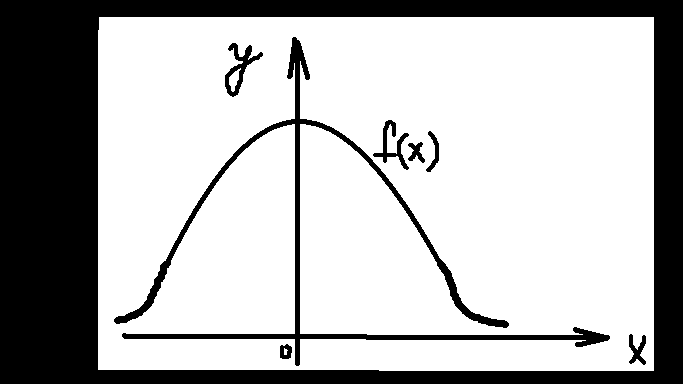 .
Для
.
Для
![]() сущ-ет тбл. значений ф-ии f(x).
При x>5
f(x)
сущ-ет тбл. значений ф-ии f(x).
При x>5
f(x)![]() 0;
f(-x)=f(x)
– функция четная.
0;
f(-x)=f(x)
– функция четная.
Интегр.
теорема:
Если вер-ть р наступления соб-я А в каж.
испытании постоянна и отлична от 0 и 1,
то вер-ть того, что число m
наступления соб-я А в n
независимых испытаниях заключено в
пределах от а до b
(включительно) при достаточно больших
n
приближенно =:
![]() ;
;
![]() ;
;
![]() ,
где
,
где
![]() - функция Лапласа.
- функция Лапласа.
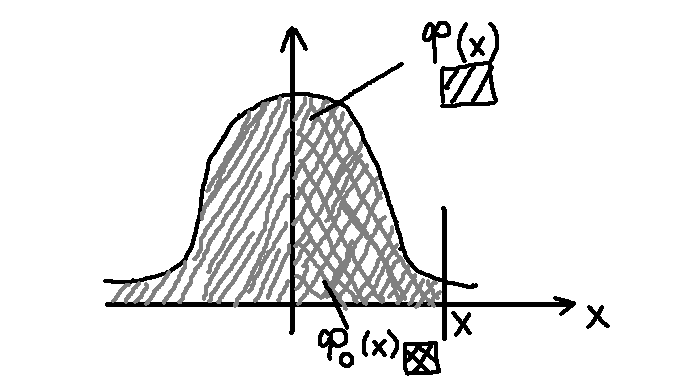 Площадь криволинейной трапеции,
ограниченной ф-ями y=f(x)
и осью абсцисс =1 => S
от
Площадь криволинейной трапеции,
ограниченной ф-ями y=f(x)
и осью абсцисс =1 => S
от
![]() до
0 и от 0 до
до
0 и от 0 до
![]() =0,5. Поэтому для сокращения исп-ся спец.
тбл.: для
=0,5. Поэтому для сокращения исп-ся спец.
тбл.: для
![]() сущ-ет тбл. зн-ий ф-ии Лапласа.
сущ-ет тбл. зн-ий ф-ии Лапласа.
![]() ;
Ф(х)=0,5+Ф0(х). При
;
Ф(х)=0,5+Ф0(х). При
![]() значение
значение
![]() Следствия: 1)Если вер-ть р наступления
соб-я А в каж. исп-ии постоянна и отлична
от 0 и 1, то при достаточно большом числе
n независ. испытаний вер-ть того, что: а)
число m
наступ.соб.А отлична от np
не более чем на величину Е>0 при-но
равна:
Следствия: 1)Если вер-ть р наступления
соб-я А в каж. исп-ии постоянна и отлична
от 0 и 1, то при достаточно большом числе
n независ. испытаний вер-ть того, что: а)
число m
наступ.соб.А отлична от np
не более чем на величину Е>0 при-но
равна:
![]() ;
б) частота m/n
соб.А в n независ.испытаниях заключается
в пределах от α до β включит.при-но равна:
;
б) частота m/n
соб.А в n независ.испытаниях заключается
в пределах от α до β включит.при-но равна:
![]() ,
где
,
где
![]() ;
;
![]() ;
в) частота m/n
соб.А отличная от вероятности его
наступления не более чем на ∆>0 по
абсолютной величине приближенно равна:
;
в) частота m/n
соб.А отличная от вероятности его
наступления не более чем на ∆>0 по
абсолютной величине приближенно равна:![]() .
.
