46. Доверительная оценка неизвестного Mx при неизвестной Dx

Дана выборка объема n предположительно отобранная из нормально распределенной генеральной совокупности с параметрами Мх и , значения которых неизвестны.

Теорема: если признак х имеет нормальный ЗР с параметрами Мх=Со, Дх= , тогда выборочная средняя имеет норм ЗР с мат ожиданием М( )=Со и Д( )=

Рассмотрим СВ

Которая распределена по закону Стьюдента с n-1 степенями свободы. Число степеней свободы определяется как общее число наблюдений минус число уравнений, связывающих этих уравнений.

При малых n для оценки дисперсии применяется формула

– исправленная дисперсия

Для заданной надежности Ɣ по таблице распределения Стьюдента определяется для которой выполняется условие:

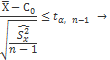
При интервальная оценка генеральной средней осуществляется по формуле:

47. Доверительная оценка неизвестной Dx при неизвестном Mx.

Для нахождения доверительного интервала для неизвестной дисперсии нормально распределенной случайной величины рассмотрим статистику

Можно показать, что эта статистика имеет ²-распределение с п-1 степенями свободы. Следовательно, справедливо равенство

которое можно переписать в виде

Таким образом, 100%-ный доверительный интервал для неизвестной дисперсии   нормального распределения с неизвестным математическим ожиданием Mx будет иметь следующий вид

где   и   - квантили распределения ² с n -1 степенями свободы. В частности, для длины лепестков ириса, учитывая, что s² =0.22, n1=49,   и , получаем, что 95%-ным доверительным интервалом для дисперсии (в предположении нормальности распределения) будет интервал (0.15, 0.34).

Заметим, что полученный доверительный интервал для дисперсии, в отличии от доверительного интервала для математического ожидания, чувствителен к отклонениям от исходного предположения о нормальности распределения.

48.Элементы общей теории проверки статистических гипотез

Опр-е : Статистической гипотезой называется любое предположение относительно генеральной совокупности ,полученное в результате анализа выборочных данных.

Стат.гипотезы:1)параметрические2)непараметрические

Опр-е: Стат.гипотеза наз. параметрической если в ней формулированы предположения относительно значений параметров расположения при условии, что закон распределения считается известным.

Опр-е: Стат.гипотеза наз. непараметрической , если в ней сформулированы предположения относительно соответствия ЗР генер-ой совокупности передполагаемому теоретическому ЗР.

Статистическая гипотеза : 1)основная 2)конкурирующая(альтернативная)

Опр-е : Стат.гипотеза наз. основной (Но),если она утверждает ,что различие между сравниваемыми величинами отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки.

Опр-е : Стат.гипотеза наз. конкурирующей если она смыслу противоречит (Н1) основной.

М(N1) = М(N2) Но

М(N1) ≠ М(N2) Н1

Пример ∆ : Но – М(Х) = М(У)

Х,У – генеральные совокупности 1 и 2 соот-но

Н1 – М(Х) ≠М(У) (1)

М(Х) ˃М(У) (2)

М(Х) ˂М(У) (3)

Выбор конкурирующей гипотезы прежде всего зависит от результатов , полученных в результате анализа выборочных данных и влияет на вид критической области .

Стат.гипотеза : 1)простые 2)сложные

Стат. Гипотеза наз . простой , если она содержит только одно предположение , т.е. ей соответствует одно распределение или одна точка пространства параметров.

Стат.гипотеза наз.сложной если она состоит из конечного или бесконечного числа простых гипотез.

Общая схема проверки статистич гипотез:

1.Определяется основная и конкурирующая гипотезы

2.Выбирается статистика критерия

3.Вычисляется значение статистикикритерия по данным выборки

4.Определяется критическая область

5.Применяется статистич.решение