41. Метод наименьших квадратов получения точечной оценки.

МНК применяется в практике статистических исследований в связи с тем, что:

Не требует знания ЗР выборочных данных
Достаточно хорошо проработан в плане вычислительной реализации.

В МНК минимизируется сумма квадратов отклонения выборочных данных от теоретических значений.

Для определения теоретической функции необходимо графически изобразить исходные статистические данные.

42. Метод моментов получения точечной оценки.

Метод моментов – приравнивание определенного числа выборочных моментов соответствующим теоретических, которые являются функциями неизвестных параметров. Число к зависит от распределения признака х, рассматривая количество моментов равно числу к неизвестных параметров и решая уравнения определяются искомые оценки параметров.

В методе моментов существует неопределенность, так как уравнения для определения параметров распределения можно получить как по начальному, так и по центральным моментам, погрешность расчетов минимальна при применении моментов более низкого порядка.

43. Понятие о доверительных оценках и доверительном интервале.

Опр: интервал, полученный по данным одной выборки, с допуском, ориентированным на накрытие им истинного значения следующего параметра с заданной надежностью называется доверительным интервалом. Границами доверительного интервала являются функции выборки, поэтому доверительный интервал также носит случайный характер.

– левая граница

– правая граница.

Оценка параметров распределения на основе доверительного интервала получило название интервальной оценки. Величина доверительного интервала непосредственно зависит от объема выборки ( с ростом n интервал сужается, т.е. становится более точным) и от заданной надежности Ɣ ( чем больше Ɣ, тем шире доверительный интервал, т.е. оценка является менее точной). Если функция выборки является несмещенным следовательно отсутствует систематическая ошибка и доверительный интервал является симметричным относительно исследуемого параметра, т.е.

- предельная ошибка выборки, которая является ошибкой репрезентативности выборки, также называют полушириной доверительного интервала

44. доверительная оценка неизвестной вероятности (npq≥10)

Выборка, относительно которой определяется частота события состоит из 0 и 1, ноль соответствует эксперименту, в которой событие не наступило, 1 - наступило. Частота события – СВ, с нормированным биномиальным ЗР в случае npq≥10 ЗР частоты события сходится по вероятности к нормальному ЗР с параметрами

Рассмотрим СВ

Которая распределена по закону Гауса. При заданной надежности Ɣ определяется критическое значение распределения Гауса, для которой выполняется условие |T|≤t

Корни квадратного трехчлена являются границами доверительного интервала. Множество значений р и р^* удовлетворяющий неравенству (3) находятся внутри эллипса, проходящего через (0,0) и (1,1), полученный эллипс – эллипс доверия.

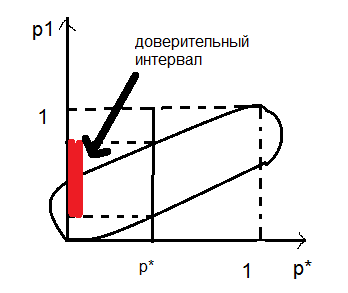
Наличие заштрихованных областей свидетельствует что при р –> 0 или 1 нельзя говорить о норм ЗР частоты m/n. Чем уже эллипс доверия, тем точнее интервальная оценка неизвестной вероятности, а с ростом надежности Ɣ и уменьшением объема выборки n доверительный интервал расширяется и получаем менее точную оценку.

Между точностью и надежностью существует жесткая взаимосвязь, чем надежнее оценка, тем менее она точна и чем точнее оценка, тем менее она надежна, при этом желательно увеличить объем выборки, тогда точность увеличивается.

45. доверительная оценка неизвестной вероятности (npq<10)

0, 1/n, 2/n, … , 1 распределена по нормальному биномиальному закону вероятности возможных значений определяется по формуле: