§ 6. Термодинамические потенциалы

Термодинамическим потенциалом называется характеристиче­ская функция, убыло которой в равновесном процессе, протекаю­щем при постоянном значении соответствующих параметров, равна максимальной полезной работе, произведенной системой. Макси­мальная полезная работа А'_mах равна максимальной работе A_mах за вычетом работы против сил внешнего давления.

Рассмотрим эти потенциалы. Воспользуемся объединенным уравнением первого и второго законов термодинамики в общем виде для обратимого процесса, в котором полная работа будет максимальной:

TdS = dU + δA_max = dU + pdV + δA’_max. (114)

Если за независимые переменные принять S и V, то уравнение (114) примет вид

-dU = δA'_max

или

-ΔU= А'_mах, (115)

т. ё. уменьшение внутренней энергии в обратимом процессе при S и V — const равно максимальной полезной работе δA_mах = δA’_max, следовательно, внутренняя энергия является термодина­мическим потенциалом.

Приняв за независимые переменные S и р, из уравнения (114) получим

— (dU + pdV) = δA’_max или —d (U + pV) = δA'_max.

Заменив (U + pV) на H, после интегрирования имеем

-ΔH= А'_{max p} (116)

т. е. уменьшение энтальпии в обратимом процессе при S = const и р = const равно максимальной полезной работе процесса. Следо­вательно, энтальпия является также термодинамическим по­тенциалом.

Определим работу при независимых переменных V и Т. За­пишем объединенное уравнение первого и второго законов термо­динамики для обратимого процесса в виде

TdS =dU + δА_max,

откуда

-(dU - TdS)= ;

-d(U-TS)= .

После замены (U—TS) на E и интегрирования получим

-ΔF = , (117)

откуда следует, что уменьшение энергии Гельмгольца в обратимом

изохорно-изотермическом процессе равно максимальной работе.

Приняв за независимые переменные р и Т из объединенного

уравнения первого и второго законов термодинамики, получим

— (dU + pdV — T dS) =

или

-d(U + pV-TS) = .

Заменив (U + pV) на H, а (H — TS) на G, имеем

—dG =

или

-ΔH = , (118)

откуда следует, что уменьшение энергии Гиббса в обратимом изобарно-изотермическом процессе равно максимальной полезной ра­боте .

Из уравнений (102) и (110) следует, что в обратном изотермиче­ском процессе изменения энергии Гельмгольца в энергии Гиббса для 1 кмоль газа

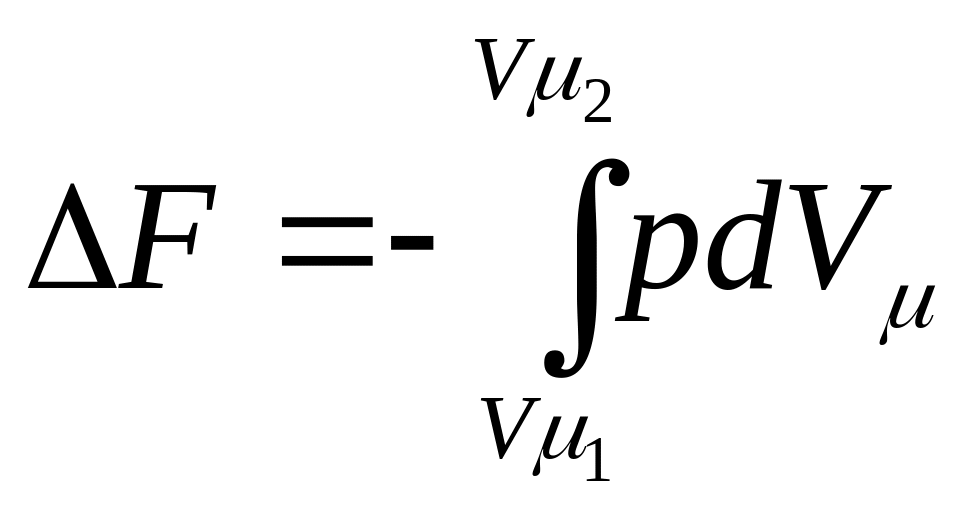
и

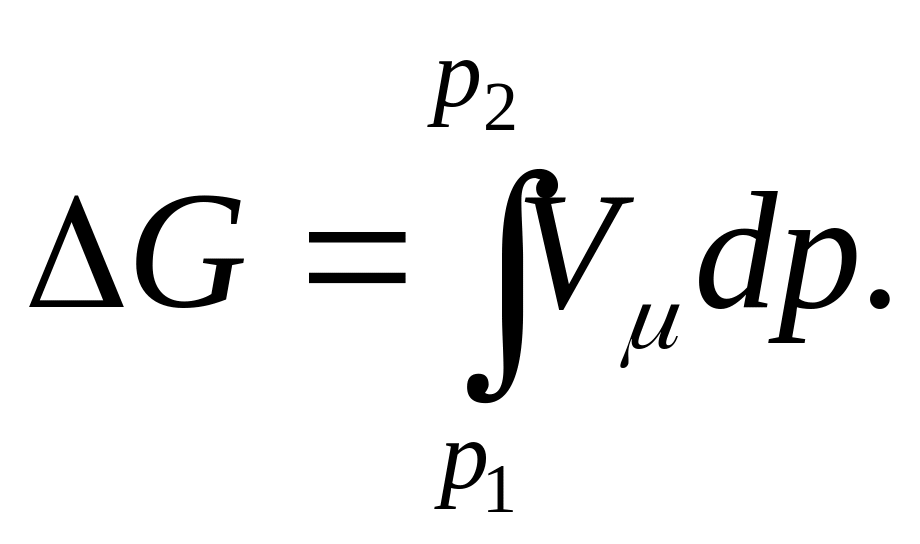
Заменив в этих выражениях р и V_μ из характеристического урав­нения Менделеева—Клапейрона

pV_μ = RT на соответствующие значения, получим изменение энергий Гельмгольца и Гиббса, а следовательно, и максимальной полезной работы в зависимости от давления и объема для изотермического процесса:

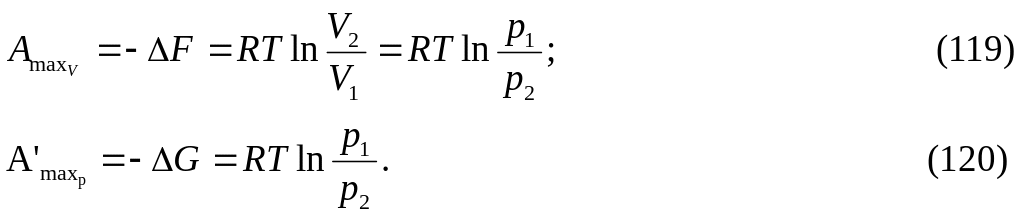Из уравнений (119) и (120) следует, что при изотермическом про­цессе для идеального газа изменения энергии Гельмгольца и энергии Гиббса одинаковы, т. е. ΔF = ΔG.