§ 2. Внутренняя энергия и ее частные производные

Примем за независимые переменные V и S. Тогда внутренняя энергия будет функцией этих переменных V =f(V, S). Так как дифференциал внутренней энергии является полным дифферен­циалом, то

(89)

Сравнив уравнения (88) и (89), можем записать

(90)

и

(91)

т. е. через первые производные характеристической функции U (по переменным V и S) определяются недостающие параметры системы (90) и (91).

Вторая производная от V (S, V) дает следующее:

(так как , откуда теплоемкость при постоянном объеме

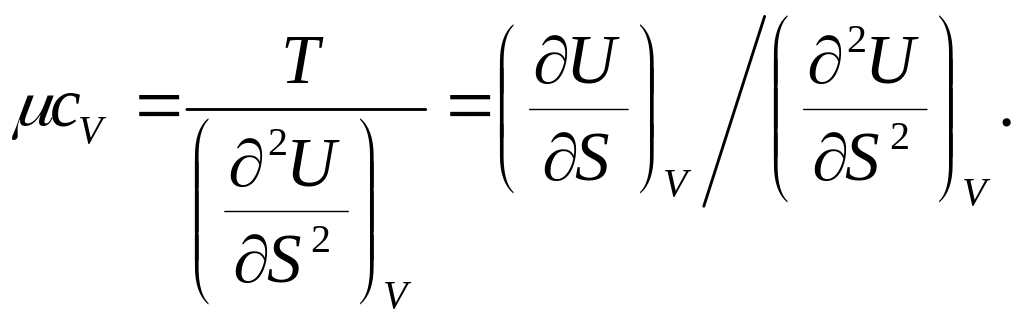(92)

Если уравнения (90) и (91) продифференцировать вторично по дру­гой переменной, то

Поэтому

(93)

Уравнение (93) связывает термические и калорические соотноше­ния системы.

§ 3. Энтальпия и ее частные производные

Примем за независимые переменные р и S, тогда энтальпия будет функцией переменных

Н = f (p, S). Полный дифференциал этой функции

(94)

Преобразуем объединенное уравнение (88). Прибавив к обеим ча­стям равенства Vdp, получим

dU + Vdp = TdS —pdV + Vdp

или

dU + Vdp + pdV = TdS + Vdp.

Откуда

d (U + pV) = T dS + Vdp.

Так как U + pV = H, то уравнение можно записать в виде

dH = TdS + Vdp. (95)

Сравнивая уравнения (94) и (95), находим

(96)

(97)

Вторая производная от Н (S, р)

(так как dS = δQ_pfT = μc_pdTfT) откуда теплоемкость при постоянном давлении

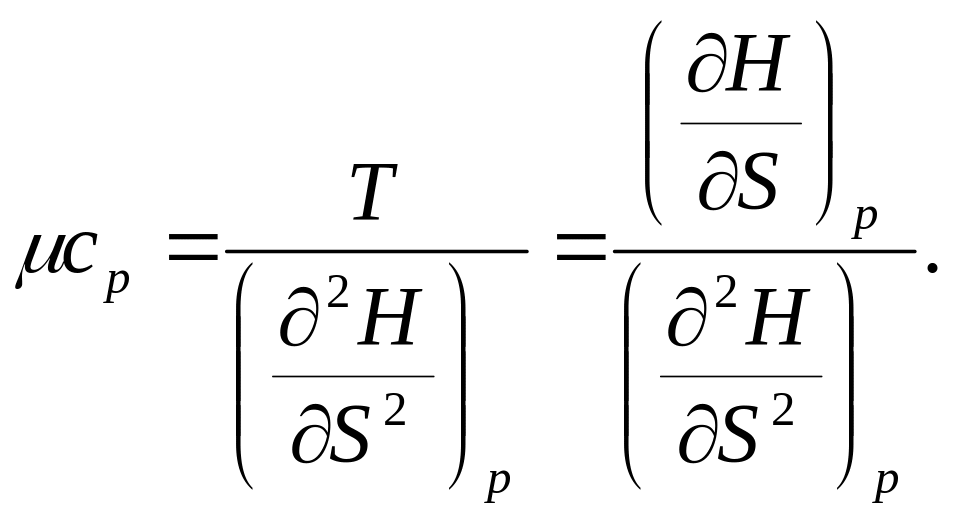(98)

Продифференцировав вторично уравнения (96) и (97) по другой переменной, получим

откуда получаем уравнение, связывающее термические и калори­ческие соотношения

(99)

или

(100)

Следовательно, через первые производные характеристической функции Н (S, р) определяются термические параметры системы по независимым переменным р и S, а через вторые — калорическая величина μc_p.