§ 5. Зависимость между тепловыми эффектами Qv и Qp

Для вывода уравнения зависимости между Q_v и Q_p восполь­зуемся соотношением

Q_p = ΔН = ΔU_p + Δ (pV),

где ΔU_p — изменение внутренней энергии термодинамической системы при осуществлении изобарного процесса. В общем слу­чае это изменение отличается от изменения внутренней энергии в изохорном процессе, т. е. ΔU_P ≠ ΔU_V, так как

V≠ const. Следовательно, . Поэтому при за­мене ΔU_V на Q_V уравнение (45) можно переписать так:

_.

В конденсированных системах разница между Q_p и Q_v незна­чительна и можно принять, что Q_p = Q_v. Однако при наличии в системе газообразных веществ разница значительная.

Если принять газы идеальными, то уравнение (45) можно записать в виде

Q_P = Qv + pΔV= Q_V + pV₂- pV₁.

Заменив в этом выражении pV₂ на n₂RT и pV₁ на n₁RT, где n₁ и п₂ — числа киломолей газообразных веществ до и после реакции, из уравнения (3) получим

Q_p = Q_v + Δ nRT (47)

Q_v = Q_p-Δ nRT, (48)

где Δn — изменение числа киломолей газообразных продуктов реакции. При Δn > 0

Q_V < Q_P.

Примером такой реакции может служить реакция образова­ния окиси углерода

2С + О₂ = 2СО, в которой Δn= 2 — 1 = 1 и Q_v = Q_p — RT, т. е. Q_v < Q_p. Термодинамическая система в этом случае совершает работу расширения за счет уменьшения внутренней энергии системы.

При Δn <0 Q_V> Q_p. Примером такой реакции могут слу­жить реакции: СО + 0,5О₂ = СО₂ или Н₂ + 0,5О₂ = Н₂О, в ко­торых Δn = 1 — 1,5 = —0,5, т. е. Δn < 0. Тогда Q_v = Q_p + 0,5RT, т. е. Q_v > Q_p.

В этом случае над термодинамической системой совершается работа внешней средой и система получает дополнительную теп­лоту.

Когда Δn = 0, тепловые эффекты Q_v = Q_p. Примером такой реакции может быть реакция СО + Н₂О = СО₂ + Н₂, в кото­рой Δn = 2 — 2 = 0. Следовательно, Q_v = Q_p.

ЗАКОН ГЕССА

Независимость теплового эффекта реакции от промежуточных стадий химических процессов была установлена русским ученым академиком Г. И. Гессом в 1840 г. на основании эксперименталь­ных данных. Это справедливо для реакций, протекающих при V, Т = const или р, Т = const. Такое утверждение является, по существу, законом сохранения энергии применительно к хи­мическим реакциям. Следует заметить, что закон Гесса — основ­ной закон химической теплодинамики был открыт еще до того, как был сформулирован первый закон термодинамики. Закон Гесса устанавливает, что тепловой эффект химической реакции не зависит от пути перехода системы из одного состояния в дру­гое, а определяется лишь начальным и конечным ее состояниями.

Таким образом, выведенные ранее соотношения

Q_V =U₂ -U₁ и Q_p =H₂ - H₁

являются алгебраическими выражениями закона Гесса.

Расчеты тепловых эффектов химических реакций описаны в ра­ботах М. В. Ломоносова, Лавуазье, Лапласа. Значительный экспериментальный материал был получен Г. И. Гессом, Н. Н. Бекетовым, Бертло, Томсоном, И. А. Каблуковым и другими учеными. Обширные исследования по определению теп­ловых эффектов химических реакций проведены В. Ф. Лугининым и его учениками.

Для определения тепловых эффектов химических реакций применяются специальные приборы — калориметры.

Закон Гесса имеет большое практическое значение, так как с его помощью можно вычислить тепловые эффекты химических реакций, экспериментальное определение которых затруднительно или практически неосуществимо. Поясним это на примере

(рис. 6).

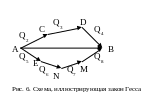
Предположим, что вещество А превращается в вещество В тремя путями: непосредственно из веще­ства А в вещество В с тепловым эффектом Q₁; через стадии С, D с тепловыми эффектами Q₂, Q₃, Q₄, через стадии Е, N, М с тепловыми эффектами Q₅, Q₆, Q₇ и Q₈. По закону Гесса суммарные тепловые эффекты одинаковы, поэтому

Q₁=Q₂+Q₃+Q₄;

Q₁₌Q₅+Q₆+Q₇+Q₈.

Тогда

Q₂+Q₃+Q₄=Q₅+Q₆+Q₇+Q₈.

Пользуясь этими соотношениями, легко вычислить тепловой эффект любой химической реакции, который невозможно полу­чить экспериментально. Например, тепловой эффект

Q₈ =Q₁-Q₅-Q₆-Q₇.

Как правило, экспериментальное определение тепловых эффектов на всех стадиях проводится с большой тщательностью, соблюдаются все предпосылки, вытекающие из закона Гесса (усло­вия, к которым приводятся начальные и конечные продукты сго­рания, одинаковый химический состав исходных продуктов и т. д.), сведены до минимума ошибки и неточности, связанные с усло­виями теплообмена экспериментальной аппаратуры с окружаю­щей средой, способами измерения температур и др., т. е. необра­тимые потери, связанные с превращением механической энергии непосредственно в тепловую, практически отсутствуют.

С помощью закона Гесса можно производить расчеты, исполь­зуя так называемые термохимические уравнения, представляю­щие собой стехиометрические уравнения химических реакций, в которых наряду с химическими формулами веществ, участвую­щих в реакции, записываются тепловые эффекты (отнесенные к одинаковым условиям). С этими уравнениями можно произво­дить алгебраические действия так же, как с любыми алгебраи­ческими уравнениями.

Стехиометрическими уравнениями или соотношениями назы­ваются численные соотношения между количествами реагирую­щих веществ, отвечающие законам стехиометрии, основные поло­жения которой вытекают из законов Авогадро, Гей-Люссака, постоянства состава, кратных отношений и др.

Из стехиометрического соотношения, например,

2Н₂ + О₂ = 2Н₂О

следует, что при образовании воды на две молекулы водорода Приходится одна молекула кислорода или в общем виде

x_aA+x_bB=x_aD, при образовании x_d молекул вещества D на x_а молекул вещества А требуется x_b молекул вещества В. Коэффициенты х_а, x_b и x_d — число молекул исходных веществ и полученных в реакции назы­ваются стехиометрическими коэффициентами.

Количество киломолей исходных и полученных веществ в хи­мической реакции пропорционально стехиометрическим коэф­фициентам. В газовых реакциях объемы и парциальные давления реагирующих веществ и продуктов реакции также пропорцио­нальны стехиометрическим коэффициентам.

Так как тепловые эффекты зависят от физического состояния реагирующих веществ и условий, при которых протекает реак­ция, то для возможности проведения термохимических расче­тов, тепловые эффекты, вводимые в термохимические уравнения, должны быть отнесены к каким-то одинаковым условиям, в про­тивном случае они несопоставимы. За такие условия принимают условия, при которых реакция осуществляется между веществами, находящимися в определенных стандартных состояниях.

За стандартные состояния индивидуальных жидких и твер­дых веществ принимают их устойчивое состояние при данной тем­пературе и давлении р = 1 атм = 760 мм рт. ст., или 1,013- 10⁵ Па, а для индивидуальных газов — такое их состояние, когда при давлении р = 760 мм рт. ст. и данной температуре они подчиняют­ся уравнению состояния идеального газа.

Широко приводимые в справочниках тепловые эффекты обычно относят к давлению р = 1 физической атмосфере (1,013·10⁵ Па) и температуре t = 25° С (298,15 К) и обозначают Q⁰_V298 и Q⁰_P298

или ΔQ⁰₂₉₈ и ΔH⁰₂₉₈.

Из закона Гесса вытекают следствия, имеющие большое прак­тическое значение.

1. Тепловой эффект реакции разложения Q_paз химического соединения по величине равен и противоположен по знаку тепло­вому эффекту образования Q_o6p этого соединения из продуктов разложения:

Q_разл=-Q_обр

2. Если из двух химических систем образуются одни и те же конечные продукты двумя различными путями, то разность между значениями тепловых эффектов химических реакций равна теп­ловому эффекту превращения одной химической системы в дру­гую. Так, например, для реакции образования вещества В из веществ А и С (рис. 7), согласно закону Гесса,

Q₁ = Q₂ + Q₃,

откуда тепловой эффект превращения вещества А в С

Q₃= Q₁- Q₂

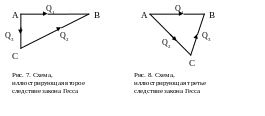
3. Если одинаковые по химическому составу системы двумя путями превращаются в различные конечные продукты, то разность между значениями тепловых эффектов, равна теплоте, по­лученной при превращении одного конечного продукта химиче­ской реакции в другой. Так, при образовании из вещества А ве­ществ В и С (рис. 8), согласно закону Гесса, Q₁ = Q₂ + Q₃ , откуда тепловой эффект перехода вещества С в вещество В

Q₃ =Q₁ - Q₂.

При термохимических расчетах особое значение имеют два вида тепловых эффектов химических реакций: теплота образова­ния соединений и теплота сгорания.

Теплотой образования принято называть тепловой эффект реакции образования данного соединения из соответствующих простых веществ в стандартных условиях.

За стандартное состояние простых веществ принимают их стабильное состояние при давлении, равном одной физической атмосфере (760 мм рт. ст., или 1,013- 10⁵ Па) и температуре 298,15 К.

В качестве примера можно привести реакцию образования бензола: из веществ в стандартных состояниях —'■ твердого угле­рода и газообразного водорода получается жидкий бензол

6С_ТВ + ЗН₂ = С₆Н_6ж.

Индексы соответственно «ж» и «тв» относятся к жидкой и твердой фазам. Индекс «г» относится к газообразному веществу, однако в расчетных уравнениях его обычно опускают.

Теплота образования, соответствующая стандартным усло­виям, называется стандартной. Данные по теплоте образования наряду с другими физико-химическими величинами приводятся в справочниках.

Так как при термодинамических расчетах определяют не аб­солютные значения внутренней энергии и энтальпии, а их изме­нение, то при определении теплоты образования какого-либо соединения начало отсчёта внутренней энергии или энтальпии можно выбрать произвольно. Так, например, в справочниках Для различных простых веществ при стандартных условиях при­нимают, что энтальпия равна нулю. К таким веществам отно­сятся С, Н₂, О₂, Cl_2(г) ,F_2(г) и др.

Таким образом, тепловой эффект образования соединений из этих веществ, например, Q_p оказывается равным энтальпии соеди­нения при искомых условиях.

Теплоту образования можно относить к любому количеству вещества. В справочниках, как правило, ее относят к 1 кмоль или 1 кг соединения.

В табл. 1 приведены значения теплоты образования веществ для некоторых распространенных химических соединений.

Теплота сгорания. Горение представляет собой сложное, быстро протекающее химическое превращение, сопровождающееся выде­лением значительного количества теплоты и, как правило, ярким свечением.

Таблица 1. Тепловые эффекты образования соединений из простых веществ при стандартных условиях

Вещество	Q0P298= ΔH0298 ·10-6 Джfкмоль	Q0P298= ΔH0298·10-3 Ккалfкмоль	Вещество	Q0P298= ΔH0298 ·10-6 Джfкмоль	Q0P298= ΔH0298·10-3 Ккалfкмоль
С (графит)	0	0	С2Н4г — этилен	52,28	12,492
Нг	217,98	52,098	С2Н6г— этан	—84,67	—20,236
H2г	0	0	С3Н8г — пропан	—103,9	—24,820
N2г	0	0	С6Нвг — бензол	82,93	19,82
Oг	429,18	59,56	С6Н6ж — бензол	49,04	11,718
OHг	38,96	9,31	СвН12г — цикло-	—123,1	—29,43
OH2г	0 -	0	гексан
	142,3	34,0	С7Н8г — толуол	50,00	11,95
COг	—110,5	—26,41	С7Н8ж — толуол	8,08	1,93
CO2г	—393,51	—94,05	C10 H8кр — нафта-	75,44	18,03
СаСО3 (кальцит)	—1206	—288,2	лин
СаО (кристалл)	—635,1	—151,8	СН4Ож — метило-	—238,7	—57,05
Н2ОГ	—241,84	—57,80	вый спирт
H2Oж	—285,84	—68,32	СН4ОГ — метило-	—202,2	—48,09
NH3г	—46,19	—11,04	вый спирт
NH3ж	—69,87	—16,7	С2Н6ОЖ — этило-	—277,6	—66,35
NOг	90,37	21,60	вый спирт
NO2г	33,89	8,09	С2НвОг — этило-	—235,3	—56,24
N2Oг	81,55	19,5	вый спирт
N2O4r	9,37	2,24	CH5Nr — метил-	—28,03	—6,70
NaO5	(12,5)	(3,06)	амин
CH4r — метан	—74,85	—17,889	C2H7Nr — диметил-	—27,61	—6,60
QH2r — ацетилен	226,75	54,194	амин

Рис. 9. Схема калориметрической «бомбы»:

1 – цилиндр; 2 – крышка; 3 – чашечка; 4 - спираль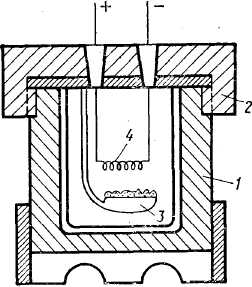

Тепловой эффект реакции горе­ния, называемый теплотой сгорания, обычно измеряют калориметрическим способом.

Теплотой сгорания соединения называется тепловой эффект реакции окисления данного соединения кис­лородом с образованием предельных высших окислов соответствующих элементов. Так, например, в орга­нических соединениях, являющихся основным топливом в тепловых двигателях, углерод окисляется до углекислого газа, водород — до водяных паров, другие вещества, входящие в соединение в незначительных количествах — до их конечных продуктов окисления.

На теплоту сгорания существенное влияние оказывают темпе­ратура и давление. Для возможности использования теплоты сго­рания в термохимических соотношениях ее нужно приводить к стандартным условиям. Теплота сгорания в этом случае назы­вается стандартной. Значение теплоты сгорания, найденное по справочнику, используется для определения тепловых эффектов реакций.

На рис. 9 приведена схема калориметрической бомбы, в кото­рой экспериментально определяют теплоту сгорания. Калориме­трическая бомба представляет собой толстостенный стальной цилиндр 1, покрытый изнутри платиной. На цилиндр навинчи­вают крышку 2. Внутри цилиндра предусмотрена чашечка 3 для навески исследуемого вещества. В цилиндр под высоким давлением нагнетают кислород. С помощью проволочки 4, нагре­ваемой электрическим током, поджигают исследуемое вещество. Бомбу помещают в калориметр, посредством которого и опре­деляют теплоту сгорания исследуемого вещества. Температуру про­дуктов сгорания «приводят» к температуре в бомбе до поджигания.

Теплота сгорания органических соединений, часто называемая теплотой сгорания топлива, является исходной величиной в рас­четах рабочих процессов тепловых двигателей. Она определяется как количество теплоты (в Дж или ккал), выделяющееся при пол­ном сгорании 1 кг массы, 1 м³ объема или 1 кмоль топлива.

Теплота сгорания топлива, если ее определить описанным выше способом, в калориметрической бомбе будет теплотой сгорания для процесса при V = const, т. е. это будет тепловой эффект Q_V.

Различают высшую и низшую теплоту сгорания топлива.

Высшей теплотой сгорания топлива Q_B называется полное количество теплоты, выделившееся при сгорании горючих частей топлива при условии конденсации водяных паров.

Низшей теплотой сгорания топлива Q_H называют разницу между полным количеством выделившейся теплоты и скрытой теп­лотой парообразования воды как имеющейся в топливе в виде примеси, так и получающейся в результате сгорания водорода.

Высшая Q_B и низшая Q_H теплоты сгорания топлива связаны между собой соотношением

-Q_h = -Q_B+r_b (9H + W) = -Q_b + 2,512·10⁶ (9H+W), Джfкг, (49)

где r_b — скрытая теплота парообразования (для технических расчетов принято r_b ≈ 2,512· 10⁶ Джfкг); 9H — количество во­дяного пара, образующегося при сжигании H (кг) водорода, со­держащегося в 1 кг топлива; W — количество влаги, содержа­щейся в 1 кг топлива, кг.

В расчетах рабочих процессов ДВС за теплоту сгорания при­нимают низшую теплоту сгорания, так как продукты сгорания, удаляющиеся из двигателя через выпускную систему, обычно имеют температуру, превышающую температуру конденсации содержащихся в них водяных паров.

В табл. 2 приведены значения низшей теплоты сгорания топлив.

На основании закона Гесса и его следствий можно составить термохимическое уравнение для определения теплового эффекта реакции через тепловые эффекты образования реагирующих веществ.

Так, например, если имеет место реакция bВ + dD = еЕ + gG, где В, D, Е, G, b, d,e, g — исходные вещества и продукты реакции

Таблица 2

Низшая теплота сгорания топлив

Топливо	Молекуляр- ная масса	Низшая теплота сгорания
	μ г, кгfмоль	Джfкг · 10-6	ккалfкг
Бензин (элементарный состав по массе	110—120	—44,0	—10 500
С = 0,855: Н = 0,145)
Дизельное топливо (элементарный со-	180—200	—42,50	—10 150
став по массе С = 0,870; Н = 0,126;
О = 0,004)
Керосин типа Т-1		—42,845	—10 230
СН4г — метан	16,042	—49,80	—11 860
С3Н8г — пропан	44,094	—46,05	—11 000
CH5Nr — метиламин	31,058	—31,20	—7 446
СгН7Нг — этиламин	45,084	—35,15	—8 340
CHeN2}K — металгидразин	46,084	—25,44	-^-6 070
C2H8N2}K — несимметричный диметил-	60,100	—32,90	—7 850
Гидразин

и их стехиометрические коэффициенты соответственно, то тепло­вой эффект этой реакции

Q_p=(eQ_обр+gQ_обрG) – (bQ_обрB+dQ_обрD)

Отсюда уравнение в общем виде

(50)

где Q_обрB, Q_обрD, Q_обрE и Q_o6pG —теплота образования соот­ветственно исходных веществ и продуктов реакдии; n_i — числа киломолей (от 1 до т), пропорциональные стехиометрическим ко­эффициентам реагирующих веществ.

Следовательно, тепловой эффект реакции равен разности теплоты образования продуктов реакции и теплоты образования исходных веществ, взятых с соответствующими стехиометрическими коэффициентами.

С помощью закона Гесса и его следствий можно также соста­вить термохимическое уравнение для расчета теплового эффекта, если известна теплота сгорания веществ, участвующих в ре­акции.

В общем виде

т. е. тепловой эффект реакции равен разности между теплотой сгорания исходных веществ и теплотой сгорания продуктов реак­ции (с учетом их стехиометрических коэффициентов).

Это можно проиллюстрировать на примере сгорания метило­вого спирта СН₃ОН (рис. 10). Теплота сгорания 1 кмоля метилового жидкого спирта

Q_2сг = — 726,49·10⁶ Дж/кмоль;

теплоты сгорания С в СО₂ и Н₂ в Н₂О_Ж соответственно равны

Q'_1cг = —393,51·10⁶ Дж/кмоль;

Q"_1cг = —285,84·10⁶ Дж/кмоль;

Q_lcг = —965,19 ·10⁶ Дж/кмоль.

Рис. 10. Схема определения теп­лово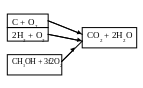 го эффекта при сгорании ме­тилового спирта

Запишем термохимические уравнения реакций горения:

C +O₂ = CO₂ + Q'_1cг;

2Н₂ + О₂ = 2Н₂О_Ж + 2Q"_1cг ;

СН₃ОН_Ж + 1,5О₂ = СО₂ + 2Н₂О + Q₂.

Для определения теплоты образования метилового спирта из уравнения С + 2Н₂ + 0,5О₂ = СН₃ОН + Q₃ сложим два напи­санных выше уравнения и вычтем третье. После некоторых пре­образований получим

С + 2Н₂ + 0,5О₂ = СН₃ОН + (Q_lcr - Q_2cr),

сравнивая два последних уравнения, заключаем, что искомая теплота образования 1 кмоля жидкого метилового спирта

Q_3обр = —238,7·10⁶ Джfкмоль.

ЗАВИСИМОСТЬ ТЕПЛОВОГО ЭФФЕКТА РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ. ЗАКОН КИРХГОФА

Для определения зависимости теплового эффекта реакции от температуры продифференцируем уравнения (44) и (46):

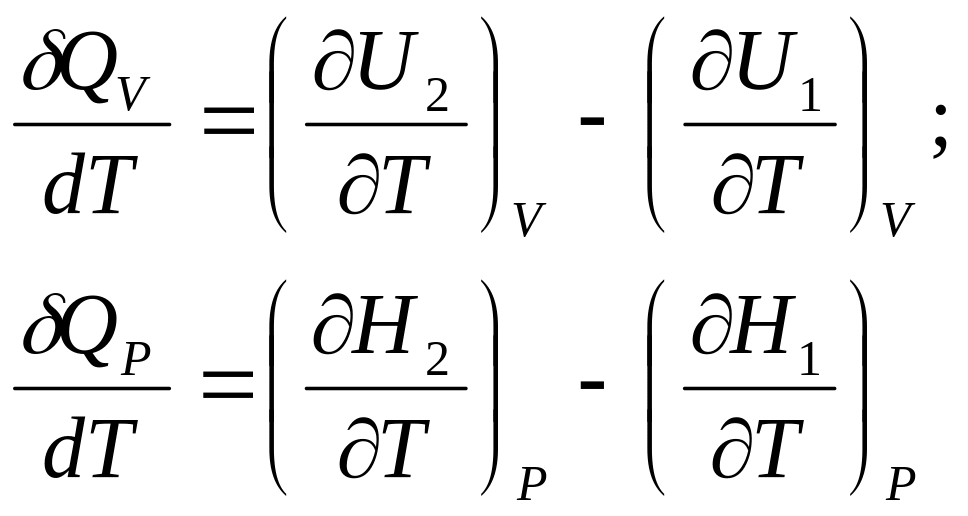₍₅₂₎

Так как выражения и для идеальных газов представляют собой теплоемкости при V = const и р = const, то в приведенных выше соотношениях члены , и

являются суммарными изохорными и изобарными киломольными теплоемкостями( μc_V1 и μс_V2) и (μc_P1 и μc_Р2) системы до и после реакции.

Подставляя значения теплоемкостей в уравнения (52), можем записать

δQ_V/dT = μс_V2 - μc_V1;

δQ_p/dT = μc_Р2 - μc_P1 (53)

и в общем виде

δQ/dT = μс_V - μc₁ = Δμc (54)

Отношения δQ_VfdT и δQ_pfdT называются температурными коэф­фициентами теплового эффекта изохорной и изобарной реакций соответственно.

Приведенные соотношения (53) и (54) выражают закон Кирх­гофа, который устанавливает, что температурный коэффициент теплового эффекта изохорной реакции равен разности суммарных изохорных теплоемкостей продуктов реакции и исходных веществ, а температурный коэффициент теплового эффекта изобарной реакции равен разности суммарных изобарных теплоемкостей продуктов реакции и исходных веществ.

Уравнение закона Кирхгофа в интегральной форме

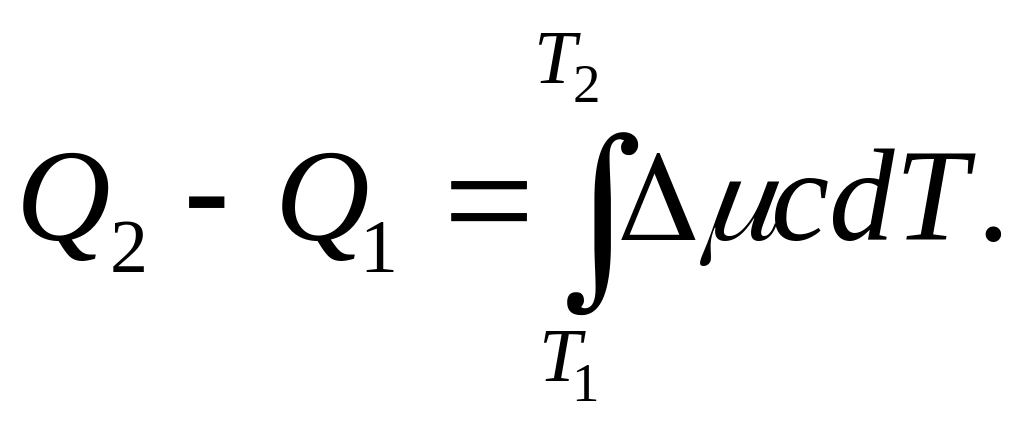
Если температуру T₁ принять равной абсолютному нулю, то уравнение Кирхгофа для процессов, протекающих при V = const и р = const, можно записать так

или в общем виде

(55)

где Q₀ — тепловой эффект реакции при T₁ = 0. Из уравнения (54) следует, что характер кривой Q = f (Т) зависит от знака прира­щения теплоемкостей Δμc.

Рис. 11. Зависимость теплового эффекта реакции от температу­ры и приращения теплоемкостей

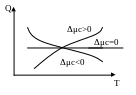
При Δμc > 0 (рис. 11) тепловой эффект реакции с повыше­нием температуры растет, при Δμc < 0 убывает, а при Δμс = О остается постоянным.

§ 8. УРАВНЕНИЕ ВИДА Q = f (Т)

Для вывода уравнения зависимости теплового эффекта от температуры Q = f (Т) необходимо в уравнении (54) раскрыть величину Δμс. Запишем реакцию вида n_bВ + n_dD = п_еЕ + n_gG, где n_b, n_d, п_е и n_g — количества кмоль веществ В, D, Е и G.

Определим суммарные мольные теплоемкости исходных (В и D) веществ и продуктов реакции (Е и G).

Если принять зависимость теплоемкости от температуры вида (17), то суммарная теплоемкость исходных веществ

μc₁=μc_B+μc_D,

где μc_B=n_b(a_b+b_bT+c_bT²+…) и μc_D=n_d(a_d+b_dT+c_dT²+…),

а суммарная теплоемкость продуктов реакции

μс₂ =μc_E + μc_G,

где μс_E = n_е (а_е + b_eT + c_eT² +…)

и μc_G = n_g (a_g +b_g Т + c_gT² +…).

Подставляя значение теплоемкостей в уравнение (54) после соот­ветствующих преобразований получим

δQfdT = (n _ea_e + n_ga_g — n_ba_b — n_da_d) + (n_eb_e + n_gb_g — n_bb_b — n_db_d) T+

+ (n_ec_e + n_gc_g — n_bc_b – n_dc_d) T²

или

откуда

.

Проинтегрировав это выражение, найдем Q:

Если принять T = T₀ ,то можно найти значение постоянной интегрирования Q₀ ⁼ const. Тогда уравнение в общем виде

Обозначим . Тогда уравнение Q = f (T) примет окончательный вид:

Q=Q₀ + αT + βT² + γT³ + … (56)

Если принять зависимость теплоемкости от температуры как сте­пенную функцию из уравнения (18), то после подстановки и соот­ветствующих преобразований получим

Q = Q₀ + αT + βT²- γ’fT, (57)

где γ' = Σ(nc’).

Приняв зависимость μc = f(Т) в общем виде μc =а + bТ + сT² + с'fT², можно, объединив уравнения (56) и (57), записать

Q = Q₀ + αT + βТ² + γT³ - γ'fT. (58)

Полученные уравнения дают возможность определять тепло­вые эффекты химических процессов при V = const и p = const при любой заданной температуре, если известны зависимости теп­лоемкостей μc_v и μc_p исходных веществ и продуктов реакции от температуры и тепловой эффект Q₀ данной реакции. Q₀ можно определить, если известен тепловой эффект данной реакции при какой-либо температуре, из соотношений

или

Тепловой эффект Q₂ реакции при заданной температуре и из­вестном Q₁ при какой-либо температуре определяется по фор­муле, которую можно получить, решая совместно уравнения

Q₁=Q₀ + αT₁ + βT₁² +γT₁³

и

Q₂ =Q₀ + αT₂ + βT₂² + γT₂³

Вычитая из второго уравнения первое, получим

Q₂ – Q₁ = α(T₂ – T₁) + β(T₂² – T₁²) + γ(T₂³ – T₁³). (59)

Уравнение (59) имеет большое практическое значение, так как с его помощью можно подсчитать тепловой эффект реакции для таких условий, при которых экспериментально его определить трудно или невозможно.

Важное значение для практики имеет также уравнение для подсчета теплового эффекта реакций по значениям средних теплоемкостей, изменением которых в небольших интервалах температур можно пренебречь:

откуда

(60)

где μс₁, μc₂, Δμc — средние суммарные мольные теплоемкости исходных веществ и продуктов реакции в пределах температур от Т₁ до T₂, соответственно и их приращение.

ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ

И ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ