Позиціонування товару

Якість низька висока	Кт ?	Р Крр
		С

Вибір позиції

Фірми

«Chocolad World»

Фірми-

конкуренти низька висока

Ціна

Р

• ТМ «Рошен»

C

• ТМ «Світоч»

Крррррр

• ТМ «Корона»

Кт

• ТМ «Конті»

?

• потенційна ніша

Рис.3.2 Схема позиціонування товару

На схемі видно, що залишається незадоволеною потреба в підприємстві, яке вироблятиме і продаватиме шоколад високої якості і за помірною ціною. Визначивши для свого товару саме цю позицію, фірма «Сhocolate world» зможе знайти своє місце на ринку.

Розділ 4. Визначення оптимальної ціни на товар на підставі проведення пробного маркетингу

Цінова політика фірми може базуватися на трьох методичних підходах: на витратах, попиті чи конкуренції. У даній роботі я використовуватиму методику ціноутворення, що орієнтована на попит, з врахуванням впливу інших методичних підходів, оскільки вони взаємопов’язані. Обраний метод базується на класичній економічній моделі, яка розглядає ціноутворення як механізм, що відповідає за ефективне розміщення і використання ресурсів. Центральним в економічній моделі є закон попиту, відповідно до якого між попитом і ціною існує обернена залежність.

4.1. Визначення взаємозв’язку між ціною і попитом

Для оцінки взаємозв’язку між ціною і попитом на свій новий товар (рівнем його збуту) фірма протягом декількох місяців проводила пробний маркетинг цього товару при різних значеннях ціни.

Зобразимо кожну пару спостережень у системі координат, де величина попиту (N) відкладається на осі Y, а ціна (Ц) - на осі X, то отримаємо кореляційне поле точок – рис. 4.1.

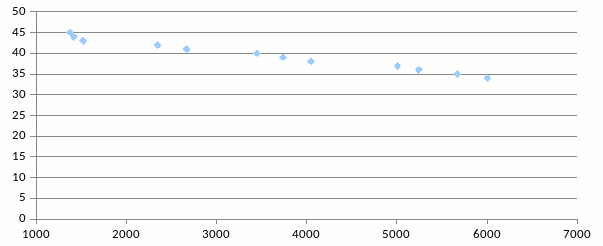
Рис.4.1. Кореляційне поле точок залежності обсягу збуту від ціни

Завдання полягає у тому, щоб скласти рівняння регресії, що встановлює взаємозв’язок між досліджуваними параметрами: ціною та обсягом попиту, що у даному випадку дорівнює рівню фактичного збуту. Оскільки зв’язок між ними близький до лінійного, то рівняння регресії буде мати вигляд:

,

де N – теоретичне значення обсягу збуту при відповідній ціні.

Використовуючи метод найменших квадратів для обчислення в₀ та в₁ слід розв’язати систему нормальних рівнянь:

де m – кількість замірів у проведеному дослідженні.

Проміжні дані для розрахунку доцільно показати у вигляді табл. 4.1.

Проміжні розрахунки для визначення взаємозв’язку між ціною та обсягом збуту

Таблиця 4.1.

Замір	Ці	Ni	Ці*ni	Ці^2	ni^2	Ni	Ni-nсер	(Ni-n)^2
1	45	1380	62100	2025	1904400	987,602	-2555,4	6530482
2	44	1419	62436	1936	2013561	1452,23	-2090,8	4371645
3	43	1524	65532	1849	2322576	1916,86	-1626,2	2644575
4	42	2352	98784	1764	5531904	2381,50	-1161,5	1349273
5	41	2671	109511	1681	7134241	2846,13	-696,94	485738,
6	40	3453	138120	1600	11923209	3310,76	-232,31	53970,9
7	39	3741	145899	1521	13995081	3775,4	232,31	53970,9

Продовженя табл. 4.1

8	38	4050	153900	1444	16402500	4240,03	696,94	485738,
9	37	5008	185296	1369	25080064	4704,66	1161,5	1349273
10	36	5242	188712	1296	27478564	5169,29	1626,2	2644575
11	35	5671	198485	1225	32160241	5633,93	2090,8	4371645
12	34	6006	204204	1156	36072036	6098,564	2555,4	6530482
Сума	474	42517	1612979	18866	182018377	42517

Отже, враховуючи дані,подані в табл. 4.1, маємо:

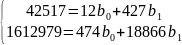
З цієї системи знаходимо в₀ та в₁

b₁= -464,632867

b₀= 21896,08159

Після цього знаходимо рівняння регресії:

21896,08159+(-464,632867)*Ц

Будуємо графік залежності N від Ц.Графік функції N=f(Ц) наведений на рис. 4.2.

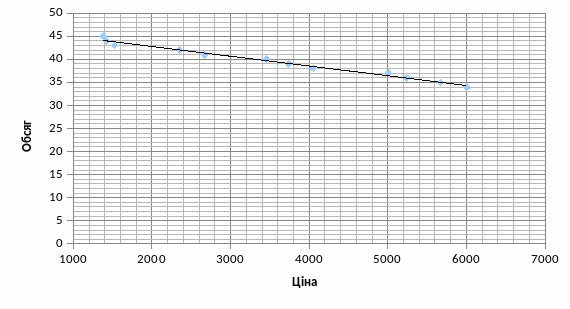
Рис. 4.2 Залежність попиту від ціни

Далі визначаємо щільність зв’язку між цими величинами, для чого обчислюємо коефіцієнт детермінації.

де – факторна дисперсія,

2572614

– загальна дисперсія,

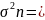2614758,576

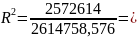0,98388208

Коефіцієнт детермінації характеризує тісноту зв’язку між даними величинами. Він має додатне значення і знаходиться в межах [0;1]. Оскільки значення R² = 0,98, то зв’язок між ціною і попитом щільний.