2. Содержание проблемных ситуаций на уроках математики

Можно выделить несколько классификаций проблемных ситуаций:

• по предмету обучения или сферы научных знаний (математике, физике и т. п.);

• по способу нахождения пути для поиска новых знаний (способов действия, новых знаний, нахождения возможности использования известных знаний и способов в незнакомых условиях);

• по уровню проблемности (очень, средне, слабо острые или не явные противоречия);

• по содержанию противоречий (например, между научными знаниями и житейскими представлениями, неожиданным фактом и неумением его объяснить и т. п.) [11].

Можно отметить самые характерные типы проблемных ситуаций на уроках, которые являются общими для всех предметов.

1. Проблемная ситуация появляется, когда ученики не знакомы со способом решения задачи, не знают ответа на вопрос, не могут разъяснить новый факт из жизни или учебной ситуации. Ученик понимает, что ему не хватает известных знаний для разъяснения нового факта [15]. Данный тип считается самым популярным.

Например, урок в 7 классе по геометрии на тему «Трапеция».

Задач: Дана трапеция , в которой , 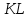- средняя линия, Основание , , . Найти Р трапеции .

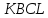Решая задачу, находят боковые стороны новой трапеции, а вычислить длину второго основания – средней линией старой трапеции, не хватает знаний о трапеции. Получается столкновение учеников с желанием решить задачу и не хваткой изученного ранее материала.

2. Проблемные ситуации появляются при столкновении учеников с необходимостью использования уже изученного знания в неизвестных новых практических условиях. Чаще всего, преподаватели формируют данные условия не исключительно для того, чтобы ученики смогли использовать собственные знания в практической работе, но и столкнулись с случаем их нехватки.

Например, уроком на тему «Объем усеченной пирамиды»

На предыдущем уроке задается ученикам задание для домашней работы: Отыскать в окружающей жизни примеры использования усеченной пирамиды. Найти ее объем.

Учитель приводит пример, для железнодорожной насыпи нужно заранее вычислить ее объем, чтобы узнать нужное количество строительных материалов, что показывает практическую важность домашней работы.

Следующий урок начинается с беседы. Ученики как примеры усеченной пирамиды называют формы щебня, картонных коробок, детали машин и тому подобное. Объясняют, как пытались найти решение, но найти объем усеченной пирамиды не поучается, что влечет проблемную ситуацию и желание найти решение проблемы [15].

Итак, процесс получения новых знаний возник в ходе работы над заданием учителя в домашних условиях, в жизненных случаях, раскрывшая важную проблему, которая выявила противоречия между появившейся познавательной потребностью и желанием ее удовлетворения при знаниях, которые уже получены ранее. Тут заметен элемент перспективности обучения; домашнее задание предусматривает подготовку к изучению новых знаний; повторения изученного идет не в виде повторного переписывания упражнений или чтения данных преподавателем страниц учебника, а в виде самостоятельной работы, которая содержит решение появившейся проблемы теоретической или практической задачи.

Проблемная ситуация с легкостью появляется в таком случае, если у нее есть противоречие между практической неисполнимостью избранного способа и теоретически возможным путем решения задачи [11].

Дидактические цели проблемных ситуаций:

1. обратить внимание учащегося к задаче, учебному материалу, вопросу, повысить познавательный интерес у него и иные мотивы деятельности;

2. поставить ученика перед такого рода познавательным затруднением с продолжение, активизируемое мыслительную деятельность;

3. помочь ученику выяснить в задании, вопросе, познавательной задаче главную проблему и построить план нахождения путей выхода из появившегося затруднения; привлечь интерес учащегося к эффективной поисковой деятельности;

4. помочь ученику выяснить границы повторяемых ранее изученных знаний и показать направление нахождения более рационального пути выхода из ситуации затруднения.

Правила необходимые для создания проблемных ситуаций.

1. Перед учениками нужно поставить такое практическое или теоретическое задание, чтобы создать проблемную ситуацию, требующее овладения новыми умениями и открытия новых неизвестных знаний; в данном случае может говорится общем способе деятельности, об общей закономерности или общих случаях осуществления деятельности. Интеллектуальным способностям ученика задание должно соответствовать. От уровня новизны материала преподавания и от степени его обобщения зависит степень трудности проблемного задания.

2. До объяснения изученного материала дается проблемное задание.

3. Проблемными заданиями могут являтся:

• усвоение;

• постановка вопроса;

• практические здания.

4. К проблемной ситуации может привести проблемное задание лишь в случае учета вышеназванных правил.

5. Любая проблемная ситуация может быть создана разными типами заданий.

6. Весьма трудную проблемную ситуацию преподаватель направляет с помощью указания ученику причин не проделывания выданного ему практического задания или нет возможности объяснить им тех или иных фактов. Например, «Вы не могли начертить треугольник с тремя известными углами, потому что в данном задании было не выполнено одно из главных правил, которые касаются треугольников» [2].

Подготовленность учащегося к проблемному учению формируется, главным образом, его умением заметить сформулированную преподавателем (или появившуюся в процессе урока) проблему, обозначить ее, отыскать пути решения и решить рациональными приемами.

Существует несколько выходов из проблемной ситуации:

1. преподаватель сам выдвигает и решает проблему;

2. преподаватель сам выдвигает и решает проблему, при этом привлекает и учеников к обозначению проблемы, выдвижению возможных предположений, доказательству гипотезы и проверке решения;

3. Ученики сами выдвигают и решают проблему, но при участии (полной или частичной) преподавателя;

4. Ученики сами выдвигают проблему и решают ее, не прибегая к помощи преподавателя (но, обычно, под его руководством) [2].

Большое количество преподавателе й понятие «проблема» уподобляют понятиям «задача» и «вопрос», проблему в обучении соединяют с проблемой в общеупотребительном ее значении.

К предлагаемой проблеме нужно предъявить небольшое количество требований. Проблемная ситуация не возникнет, если хотя бы одно из этих требований не выполнить.

1. Пониманию учеников проблема обязана быть доступной. Дальнейшая работа над задачей бесполезна, если до учащихся не дошло понимание задачи. Поэтому, проблема должна быть создана в знакомых ученикам терминах, для того чтобы каждый или, во всяком случае, большая часть учащихся поняли суть данной проблемы и средства для ее решения.

2. Простота поставленной проблемы. Если поставленную проблему большей части учеников не получится решить, понадобится потратить на много больше времени или решать данную проблему самому преподавателю.

3. Должна привлечь внимание учеников формулировка проблемы. Само собой, важным в формировании интереса является математическая особенность дела, но очень значимо выбрать и нужное словесное представление. Форма развлекательного типа часто содействует успеху решения проблемы.

4. Довольно важной ролью считается естественность формулировки проблемы. Если учеников нарочно предупредить, что будем решать проблемную задачу, в данном случае ситуация может не создать у них интереса при понимании, что будет нужно перейти к наиболее трудному [12].

Одним из наиболее важных условий удачной создания проблемы и формирования самостоятельной познавательной работы учеников является знание преподавателем главных требований к учебной программе.

По следующим этапам осуществляется формулировка учебной проблемы:

1. анализируется проблемной ситуации;

2. формулировка проблемы - понимание сути затруднения;

3. на словах формулируется проблема.

Для преподавателя учебная проблема не является проблемой. Преподаватель вводит перед учащимися проблемную задачу или проблемный вопрос. Данная формулировка ведет к появлению проблемной ситуации, принятию учащимся проблемы, которая была сформулирована и поставлена преподавателем.

Формирование проблемного обучения рассчитывает использование таких приемов и методов обучения, приводимые к появлению взаимно связанных между собой проблемных ситуаций и как следствие давали возможность выбора соответствующих методов учения.

Но все же формирование проблемных ситуаций и поисковой работы учеников может быть не во всякой ситуации. Это может быть в таких видах учебно-познавательной активности учеников, как: решение приготовленных нешаблонных задач; формирование задач и их решение; логический анализ текста; сочинение; ученическое исследование; конструирование; рационализация и изобретение и другие.

Судя из идеи формирования познавательной самостоятельности учеников, все различные виды современного урока, основанные на принципе проблемности, разделяются на проблемные и не проблемные.

С психологической точки зрения проблемным необходимо принимать урок, на котором преподаватель специально формирует проблемные ситуации и создает деятельность учеников по самостоятельному созданию учебных проблем и их решению или самостоятельной постановке проблемы и решает их, что показывает ученикам логику передвижения мысли в поисковой ситуации.

Синтетичность, комплексность является дидактическим (внешним) показателем проблемного урока. Суть синтетичного урока лежит в том, что актуализация пройденного, обычно, уходит с формулирования нового материала, идет постоянное повторение навыков, умений и знаний в новых сочетаниях и связях, что присуще именно для проблемного урока [12].

Для современного урока структурными элементами считаются:

1. повторение изученных знаний учеников (что значит не только воспроизведение уже изученных знаний, но и использование их нередко в новый неизвестных ситуации, активизирование познавательной деятельности учеников, участие учителя);

2. освоение способов действия и новых знаний (в понимании наиболее точном, чем понятие «изучение нового материала»);

3. развитие умений и навыков (включающих и закрепление, и специальное повторение) [12].

Данная структура передает и главные этапы обучения, и этапы формирования современного урока. Так как особенностью проблемности урока считается существование в его структуре этапов поисковой работы, то они и показывают внутреннюю часть структуры проблемного урока:

1. появление проблемной ситуации и создание проблемы;

2. формулировка предположений и аргументация гипотезы;

3. доказательство гипотезы;

4. проверка верности решения проблемы [12].

Поэтому, структура проблемного урока, которая представляет и себя сочетание внутренних и внешних элементов процесса преподавания, формирует возможности контролирования самостоятельной учебно-познавательной работы ученика.

В пределах проблемного обучения в педагогике изучаются общепедагогические проблемы, а также и проблемы обучения некоторым предметам. К проблемам педагогики математики это относится в особенности.

Только на уроках математики создается положительная атмосфера для введения элементов проблемного обучения, потому что проблемным способом разумно изучать данный материал, содержащие причинно-следственные зависимости и связи и направленные на формирования законов, понятий и теорий.

Примерная схема формирования урока математики в виде проблемного обучения:

1. Формирование проблемной учебной ситуации (формальной или настоящей) для того чтобы создать у учеников интерес к этой учебной проблеме и дать мотивацию целесообразности ее исследования.

2. Введение познавательной задачи (или нескольких задач), которые возникают из созданной проблемной ситуации, точная формулировка задачи.

3. Изучение различных условий, которые характеризуют выдвинутую задачу, рассмотрение возможностей моделирования ее условия или замены данной модели наиболее легкой и наглядной.

4. Процесс решения поставленной задачи. Рассмотрение задачи в общем и по частям, выделение несущественного и существенного в ее условиях, понимание в возможных трудностях при ее решении, нахождение подзадачи и последовательность ее решения, зависимость данной задачи с знаниями и опытом которые уже имеются Создание направлений которые могут быть для решений главной задачи, выборка, передача знакомых теоретических положений, которые могут быть применимы в данном направлении решения задачи, сравнительная оценка пути решения и выбор единственного из них, формирование плана решения задачи в данном направлении и его применения в целом, детальное применение плана решения задачи и аргументация верности всех шагов решения задачи, которое возникает.

5. Рассмотрение получаемого решения задачи, обсуждение его итогов, выделение нового знания.

6. Использование нового знания с помощью решения определенных выбранных учебных задач для его освоения.

7. В пределах данной проблемной ситуации обсуждаются возможные расширения и обобщения результатов решения задачи.

8. Исследование решения задачи, которое получилось, и нахождение иных менее затратных или более красивых способов ее решения.

9. Выделение итоговых результатов проделанной работы, выявление значимого в содержании, результатах, способах решения, рассмотрение возможных перспектив использования опыта и новых знаний [15].

Схематический план, который дан, создания проблемного урока математики (как и любой иной) активен (с учетом определенной характеристики той или другой учебной проблемы). Он осуществляется частично или полностью, некоторые пункты плана могут соединится вместе и так далее.

Пример урока в 8 классе по теме «Свойство медиан треугольника» в форме проблемного обучения.

Тип урока: урок открытия нового знания.

Цели:

• образовательная: выработка у учащихся навыков и умений, формирование новых понятий и знаний; в частности изучение теоремы о средней линии и теоремы о медианах треугольника и научиться использовать их при решении задач;

• воспитательная: развивать аккуратность, целеустремленность и самостоятельность в ходе решения задач;

• развивающая: формировать умение определять проблему, формулировать проблему, находить способы ее решения.

Ход урока (таблица 3):

Таблица 3

Этапы урока	Деятельность учителя	Деятельность учащихся	Комментарии
Организационный этап (1 мин)	Здравствуйте, ребята! Кто готов к уроку? Присаживайтесь, запишите число, классная работа.	Приветствие.
Актуализация знаний (4 мин)	В начале занятия, проведем теоретический опрос. Что такое средняя линия треугольника? Какими свойствами обладает средняя линия треугольника? Какие треугольники называются подобными? Сформулируйте первый признак равенства треугольников	Это отрезок, соединяющий середины 2-х сторон треугольника. Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине. Треугольники, у которых соответственные углы равны, сходственные стороны пропорциональны. Если два угла одного треугольника равны соответственно двум углам второго треугольника, то такие треугольники подобны.	На этапе актуализации знаний проводится устный опрос учащихся, о ранее изученном материале.
Мотивация и постановка проблемы (8 мин)	Решение задач на готовых чертежах. Устно с обсуждением решений. 1. Найти: а) EF, если BC=10,6 см; б) BC, если EF=4,2. 2. ABCD – трапеция. Найти: MP. (Ответ MP=5 см.) 3. Найти: В1О и А1О. Не получается, давайте вместе разберемся, каким образом нам найти эти отрезки. Какое мы можем сделать предположение о пересекающихся отрезках? Давайте, попробуем, используя уже имеющиеся знания выяснить, в каком отношении они пересекаются?	1.Ответ: а) EF=5,3; б) ВС=8,4 2. Ответ: MP=5 см. 4. не получается Они пересекаются в определенном отношении.	На этапе мотивации учащиеся, отвечая на задания, плавно переходят к проблеме, на которую необходимо найти ответ. И переходят к теме урока.
Изучение нового знания (15 мин )	Чем является отрезок B1A1? Какие свойства средней линии нам известны? B1A1||AB, что можно сказать об углах A1B1B и B1BA? Что мы можем сказать о AOB и A1O B1? Что следует из подобия? AB: B1A1= OA: A1O= OB: B1O Теперь мы можем найти нужные отрезки?	Средней линией ABC Средняя линия параллельна одной из сторон и равна ее половине Они равны, как внутренние накрест лежащие Они подобны, т.к. у них 2 пары равных углов. 2:1=OA:A1O=OB:B1O Да, B1О=4,5 и A1О=3	Через лекцию-беседу учащимся удается ответить на заданный вопрос. В случае затруднения учащимся задаются наводящие вопросы.
Закрепление нового материала (15 мин)	В ходе решения задачи мы с вами доказали очень полезную теорему, давайте её запишем: Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1 , считая от вершины. Мы доказали, что две медианы делятся точкой пересечения в отношении 2:1, считая от вершины. То, что третья медиана и одна из этих двух делятся точкой пересечения в том же отношении, доказывается аналогично. Это значит, что все 3 медианы пересекаются в одной точке. Дано: ABCD – параллелограмм AM=MB, AC=18см Найти: AK, KC Проведем диагонали ABCD Что нам известно о диагоналях параллелограмма? Рассмотрим ABD Чем являются отрезки AO и DM? Какое свойство медиан мы только что изучили? В равнобедренном треугольнике АВС О – точка пересечения медиан. Найдите расстояние от точки О до вершины А данного треугольника, если АВ=ВС=10 см, АС=16 см. Вычислите медианы треугольника со сторонами 25 см, 25 см, 14 см.	Они точкой пересечения делятся пополам Медианами ABD Они точкой пересечения делятся в отношении 2:1	На этапе закрепления нового материала учащимся предлагается решить одну задачу совместно с учителем, затем учащиеся сами решают подобные.
Рефлексия (2 мин)	Итак, наш урок подходит к концу. Что для вас сегодня было новым? Как вы оцениваете сегодня свою работу на уроке? Домашнее задание: (записано на доске)	Отвечают на вопросы, высказывают свои мысли, записывают домашнее задание.