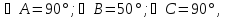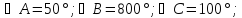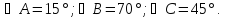2. Определение проблемного обучения. Компоненты и особенности проблемного обучения

Под проблемным обучением В. Оконь понимает «совокупность таких действий, как организация проблемных ситуаций, формулирование проблем, оказание ученикам необходимой помощи ученикам в решении проблем, проверка этих решений и, наконец, руководство процессом систематизации и закрепления приобретённых знаний» [20].

Под проблемным обучением можно иметь ввиду такой тип обучения, которому привносят иные особенности научного познания [3].

И.Я. Лернер суть проблемного обучения представляет в том, что «учащийся под руководством учителя принимает участие в решении новых для него познавательных и практических проблем в определённой системе, соответствующей образовательно-воспитательным целям школы» [12].

Некоторые педагоги на основе обобщения практической деятельности и разбора итогов теоретических исследований выдвигают следующее определение понятия «проблемное обучение»: «Проблемное обучение – это тип развивающего обучения, в котором сочетаются систематическая самостоятельная поисковая деятельность учащихся с усвоением или готовых выводов науки, а система методов построена с учётом целеполагания и принципа проблемности.» [17].

Проблемное обучение – это обучение, при котором учитель предоставляет оптимальное сочетание их самостоятельной деятельности с усвоением готовых выводов науки, регулярно создавая проблемные ситуации и организуя работу обучающихся по решению учебных проблем. [17].

Проблемное обучение помогает подъему интеллекта обучающихся, его эмоциональной сферы и образованию на данной основе мировоззрения. Самое важное различие проблемного обучения от объяснительно-иллюстрационного традиционного в этом и заключается. Отечественные психологи А.И. Матюшкин, З.И. Калмыкова, Т.В. Кудрявцев и другие создали психологические основы так называемого проблемного обучения в его некоторых вариациях. Идея заключается его в следующем. Обучающимися предлагается проблема, познавательная задача, и обучающиеся при прямом участии учителя или без чьей-либо помощи разрабатывают пути и способы ее решения [16, С. 289]. Они выдвигают предположение (гипотезу), планируют и обдумывают способы проверки ее достоверности, обосновывают, экспериментируют, наблюдения, подвергают анализу их результаты, размышляют, доказывают.

Чтобы разобраться в сути проблемного обучения стоит изучить самому древнему примеру – к тому, как обучал Сократ своих учеников примерно две с половиной тысячи лет тому назад. В одном из диалогов Платон рассказывает, как к Сократу явился юноша Феаг, чтобы выяснить, как и у кого научиться быть мудрым. И Сократ, вместо того, чтобы дать ответ молодому человеку на вопрос, начинает спрашивать его, что же он понимает под мудростью, чего же на самом деле желает.

Сократ задавал вопросы ученику, излагая их так, чтобы ученику было над чем поразмышлять, в то же время, чтобы было достаточно знаний ответить на вопрос или отыскать ответ в ходе размышлений. Выстроенная цепочка связанных между собой вопросов, любой из которых является логическим следствием главного, первого, заданного ученику, вынуждает, отыскав ответы на эти вопросы отбросить, наконец, неверное мнение и утвердиться в истинном. Такого рода диалоги назвали сократические или эвристические, а в современной трактовке - развивающие [2].

В условиях современного обучения, ученики направляются в школу учиться в соответствии с программой учебной работы, а не сами подходят к учителям с вопросами. Создание проблемы и вопросов, которые им нужно выяснить - работа учителя. Следовательно, проблемное обучение, в основном, явление в школе неестественное, которое идет не от ученика, разыскивающего ответ на волнующий его вопрос, а от преподавателя, обеспокоенного тем, как бы вызвать интерес учащихся к учебной работе [4].

Суть проблемного обучения заключается в поисковой работе учащихся, начинающейся с постановки вопросов, которые закладываются в учебных программах, потом по порядку предлагаемых в учебниках, в передаче и объяснении знаний учителем, в различной независимой и самостоятельной работе учеников.

Данный метод гарантирует вовлеченность обучающихся в решение волнующей их проблемы. Следует устроить проблемную ситуацию, чтобы учебная проблема получилась для обучающихся именно волнующей, необычной. Определённое психическое состояние или интеллектуальное затруднение, появляющееся при невозможности разъяснить привлеченное внимание явление, факт, процесс при помощи знакомых знаний или осуществить нужный шаг знакомым способом называется проблемной ситуацией.

Итак, самое главное в проблемной ситуации – озадаченность, удивление тому, что только что появившийся факт опровергает имеющиеся правильные знания, точнее с их помощью не может быть разъяснён.

Мышление каждый раз начинается с вопроса или проблемы, с противоречия, удивления или озадаченности. Данной проблемной ситуацией формируется вовлечение индивидуума в мыслительный процесс.

Существуют разные способы создания проблемных ситуаций:

• представляя несоответствие нового факта известному знанию,

• сравнивая об одном факте противоположные точки зрения,

• представляя «невозможность» применения теоретических знаний в некоторых нестандартных условиях,

• побуждая к предсказанию грядущего развития событий завершившегося произведения или их выстраивания в других условиях,

• выдавая упражнение сравнить несравнимые поначалу факты и т. п.

Существует огромное число литературы о вариантах способов создания и способов разрешения проблем [11]. Построением проблемы в общем виде завершается проблемная ситуация. В проблемном вопросе совместная проблема уточняется. Плохо сформулированный вопрос может убить возникший интерес к разбираемой области незнакомого, лишить всякого смысла все предыдущие усилия учителя. Это, к примеру, наблюдается, если вопрос очень сложный, и обучающиеся считают полную бесперспективность нахождения выхода из проблемной ситуации, а еще в таком случае, когда вопрос очень простой.

Как следует верно выраженные вопросы конкретизируют, уменьшают круг неизвестного, что собственно следует узнать для решения проблем. Следовательно, педагог «должен достичь того, чтобы ученик:

• точно понял определённую практическую или теоретическую трудность,

• понял сформулированную учителем проблему или сформулировал сам,

• захотел сам найти выход из проблемы,

• сумел это сделать» [11, С. 32].

Учитель создает проблемную ситуацию и формулирует проблемные вопросы и проблему. Дальше он раскрывает путь научного поиска, приводимый к её решению, или описывает современные способы её решения. В первом случае учитель заинтересовывает учащихся к решению полностью или частично проблемы, а во втором – всё полностью объясняет сам, постановкой вопроса гарантируя следование обучающихся путём его размышлений и доказательств.

П.Ф. Каптерев связал понимание обо всех этих разных, но которые имеют много общего, вариантах деятельности учителя на уроке общим названием – генетическая форма педагогического метода [3]. В. Оконь первый вариант называет классическим проблемным методом, а, кроме того, характеризует ещё ситуативный метод, метод случайностей, микропреподавание, банк идей [20]. И.Я. Лернер и М.Н. Скаткин считают эти варианты как частично-поисковый метод, проблемное изложение и исследовательский метод [12]. В деятельности учителя на уроке и в воспитательной работе во внеурочное время любой из них может быть использован: проблемы нравственности, эстетические и другие имеют ту же природу, что и проблемы в истории и литературе, физике или биологии.

Не нужно исключать полностью объяснительно-продуктивные методы. Получение сведений информационного характера, приумножение знаний о фактах и т. п. более продуктивно обеспечиваются применением репродуктивных методов, не связанных с расходованием столь важного количества времени, как при применении методов проблемного обучения. Большое количество знаний по математике, истории, языку и иным предметам приобретаются как раз репродуктивным способом, как и большая часть умений на уроках различных дисциплин. Объяснительно-иллюстративный метод иногда бывает наиболее продуктивным, чем проблемные методы, при овладении слишком трудным для обучающихся материалом.

Итак, ведущим к общему и специальному развитию, т.е. развивающим обучением можно назвать именно такое обучение, упираясь на знания закономерностей формирования мышления, учитель особыми педагогическими средствами управляет целенаправленной педагогической работой по развитию мыслительных способностей своих обучающихся в процессе освоения ими основных положений наук. Данное обучение и есть проблемное [3].

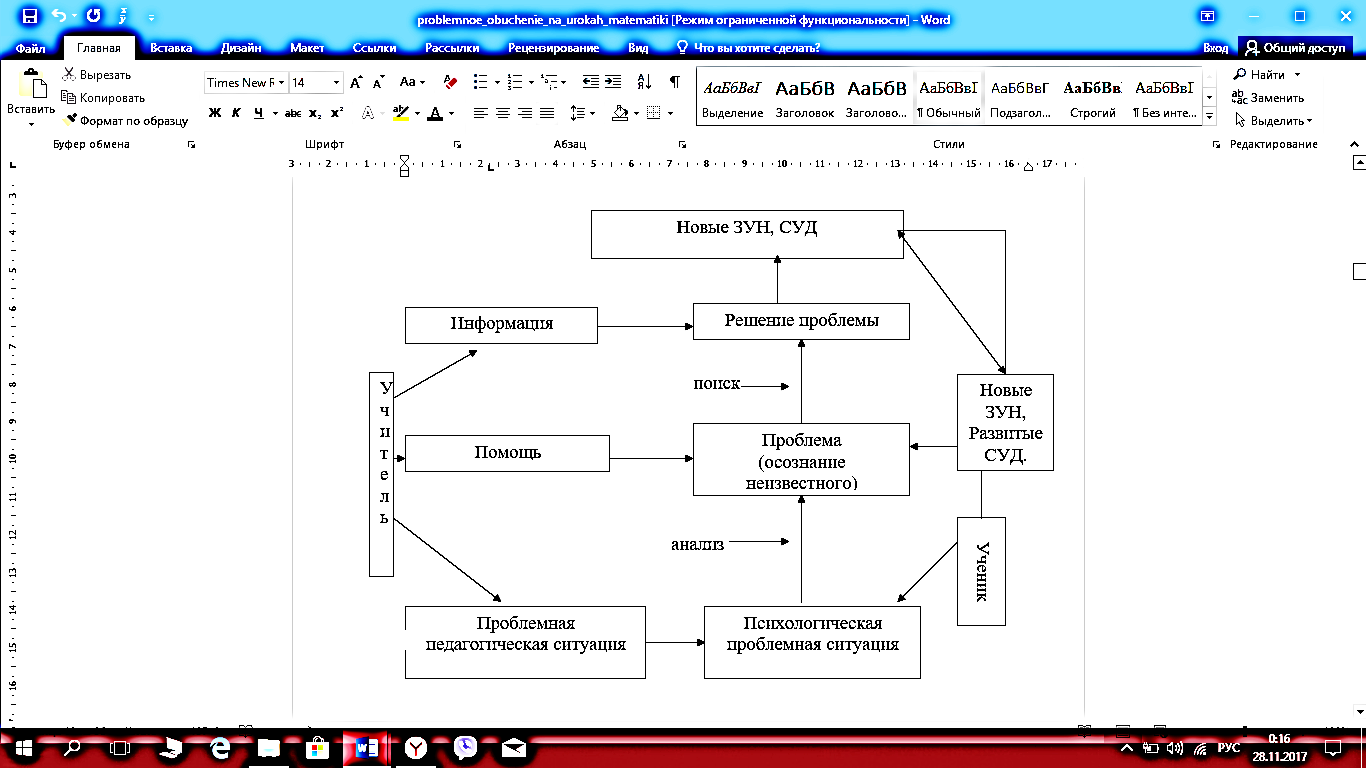
Рисунок 1 – Графическое представление процесса проблемного обучения

Проблемное обучение строится на аналитико-синтетической работе учащихся, осуществляемой в размышлении, рассуждении. Это исследовательский, эвристический тип обучения с высоким развивающим потенциалом. В таблице 1 приведены сравнительные черты проблемного обучения.

Таблица 1 – Различие традиционного от проблемного обучения

Сравнимые признаки	Традиционное обучение	Проблемное обучение
Цели	Получение знаний учениками своим трудом.	Поучение знаний при помощи учителя.
Этап урока № 1	Привлечение внимания учащихся
Этап урока № 2	Повторение ранее изученного (актуализация): учитель задаёт наводящие вопросы для того чтобы повторить ранее пройденный материал.	Обращение к прошлому опыту (например, учитель вспоминает, что степенную функцию обучающиеся уже проходили, но сейчас уже идёт повторение свойств, рассматриваются ситуации, где она применяется, построение графиков.
Этап урока № 3	Изучение нового материала: учитель раскрывает тему сам, приводит различные примеры, далее требует от учеников.	Обдумывание темы в группе: класс разделяется на группы, поначалу идёт обсуждение темы в группе, далее всем классом.
Этап урока № 4	Закрепление: преподаватель дает ученикам определённые задания по данной теме, и ученики закрепляют полученные знания в практической работе.	Разрыв – время, в которое ученики должны понять, что их знаниях с пробелами, которые им следует восполнить самим.
Этап урока № 5	Вторичное закрепление: педагог даёт уже более трудные задания для закрепления данной темы.	Рефлексия – определение степени усвоения полученных знаний.
Этап урока № 6	Подведение итогов урока

Сущностью понятий и содержанием раскрываются дидактические основы проблемного обучения.

Проблема – это вопрос, который следует из знаний, имеющихся у обучающихся, строится на них. И в то же время проблема подтверждает об их недостаточности, а значит, потребность в дальнейшем поиске для получения конечного полного представления об объекте изучения. Проблемой для обучающегося не может стать вопрос без опоры на жизненный опыт обучающегося. С преодолением противоречий всегда должен быть связан проблемный вопрос. Данные противоречия ставятся основой для получения проблемной ситуации и представления проблемы.

В учебных программах, в изложении знаний учителем, в самостоятельной работе учащихся и т. д. должен проявляться проблемный подход в обучении. При этом следует учитывать, что не любом вопрос и не любой без чьей-либо помощи поиск решения проблемы надо зачислять к проблемному обучению.

Основными понятиями проблемного обучения считаются: «проблемная ситуация», «проблемная задача», «проблема», «проблемность», «проблематизация» [2].

Проблемная ситуация – основа проблемного обучения, при помощи которой пробуждается познавательная потребность, мысль, активизируется мышление.

Проблемная ситуация - это интеллектуальное затруднение человека, возникающее в случае, когда он не знает, как объяснить возникшее явление, факт…не может достичь цели известным ему способом действия.

Проблемная ситуация - это не просто психическое состояние затруднения у субъекта и, не только объективная реальность, которая сразу становится проблемной, как только человек встретился с нею. Она имеет свои существенные признаки, такие как:

• проблемная ситуация образует трудность, которую ученик может преодолеть только с помощью личной мыслительной активностью;

• проблемная ситуация должна быть значима для ученика;

• появление проблемной ситуации связано с интересами и предшествующим опытом учащихся;

• более общая проблемная ситуация заключает в себе ряд более частных. [24, с. 195].

Учебная проблема (проблемная задача, практическое задание, вопрос) является средством формирования проблемной ситуации.

Специальная дидактическая конструкция, строящаяся из условия и вопроса, с целью создание проблемной ситуации, называется проблемной задачей.

В процессе нахождения ответа для проблемной задачи, ученики без чьей-либо помощи приходят к неизвестным и новым знаниям или к способам их приобретения, а именно нахождение способа решения или само решение поручается учащимся.

Проблемная задача может использоваться на каком угодно этапе урока:

• при разборе домашнего задания,

• при повторении изученного материала,

• при освоении и закреплении нового материала.

Проблемность задачи является ее особенностью. В Проблемной задаче содержатся элементы, которые находятся в противоречии либо с теми знаниями, которые имеются у учеников, либо между собой. В то же время способ разрешения противоречия субъекту незнаком. Желание выйти из проблемной ситуации подталкивает учеников к решению задачи. Решение находится с разной степенью познавательного умения действовать самостоятельно. Результатом решения задачи становятся или новые знания, или новые способы работы, или то и другое. Проблемная задача решается не по алгоритму, схеме, образцу, в отличие от репродуктивной задачи, точнее она не имеет стандартного решения. Данные, требование и неизвестное (искомое) – это три основных компонента в проблемной задаче.

Проблемную ситуацию необходимо отличать от проблемной задачи. Проблемная ситуация - это особое состояние субъекта и его образование. А проблемная задача - объективная информационная система, которая предъявляется ученику извне.

Проблемную ситуацию может вызвать практическое задание, если ученики знакомым им способом действия не могут с ним справиться. В проблемном вопросе существует скрытое противоречие, которое дает возможность разных по виду ответов, неоднозначного решений. Это отличает проблемный вопрос от иных видов вопросов. В качестве одного из элементов проблемной задачи – требования – проблемный вопрос может входить в ее структуру.

В момент, когда деятельность человека «включает» мышление, проблемная ситуация становится проблемой. Выделяются следующие ступени в любом целом акте размышления:

• чувство трудности;

• отыскание трудности и её определение;

• представление идеи разрешения (формулирование гипотезы);

• формулировка выводов, которые следуют из задуманного плана решения (проверка гипотезы на логичность);

• дальнейшие эксперименты и наблюдения, которые позволяют одобрить или отказаться от гипотезы.

При обучении математике проблемность часто появляется вполне естественно, потому как каждая математическая задача и есть в некоторой степени проблема, над решением которой учащемуся необходимо задуматься. Для постановки учениками проблемных задач должны быть применимы упражнения в решении составных текстовых задач, в сравнении выражений, которые требуют применение знакомых детям закономерностей и связей в новых условиях, задания геометрического характера, часто требующие переосмысления освоенных ранее знаний и многое другое. Только в таком случае преподавание математике будет оказывать эффективную помощь в решении воспитательных, образовательных и развивающих задач обучения.

Намного больше случаев для построения проблемной ситуации предоставляет введение математических понятий, использование различных типов задач, таких как задачи с недостающими данными, с несколькими способами решений и многие другие математические задания.

Проблемность - основная ситуация совершествования объекта (мир) и субъекта (человек), может быть раскрыта как диалектическая категория, рядом расположенная с другими, или как основной признак данных категорий в развитии, или как главный принцип их деятельности, необходимости действовать, или как действия.

Проблематизация – устройство, лежащее в основе раскрытия проблемности объекта субъектом, реализованной в данной проблемной задаче.

Трудность решения проблемы двоякая. Одна трудность заключается в необходимости задействовать для решения некоторую часть предыдущего опыта, только того без которого решение не под силу. Другая заключается в потребности в тоже время открывать новые, не знакомые учащемуся звенья, которые позволят решить проблему.

Значимым является то, что формой осуществления принципа проблемности в обучении считается учебная проблема.

Дидактическая классификация учебных проблем состоит из следующих переменных:

1. место в процессе обучения;

2. область и место возникновения;

3. способы создания процесса решения;

4. политическая и общественная значимость.

Психологическая классификация учебных проблем построена на таких данных, как:

1. основные черты неизвестного и вызываемого препятствия;

2. основные черты содержания и связь неизвестного и известного в проблеме;

3. способ решения [20, С. 95].

На характере противоречия, возникающего в процессе учения, основана классификация способов создания проблемных ситуаций:

1. встреча учеников с явлениями и фактами, которые требуют теоретического разъяснения;

2. использование учебных и жизненных ситуаций, которые возникают при проделывании учениками практических упражнений, создание учебных проблемных упражнений на объяснение явления и поиск путей его практического использования;

3. побуждение учеников к анализу фактов и явлений действительности, которые сталкивают их с противоречиями между житейскими представителями и об этих фактах научными понятиями;

4. формулировка гипотез, выдвижение выводов и их проверка с помощью опытов;

5. познавательное затруднение возникает благодаря побуждению учеников к сравнению, сопоставлению и противопоставлению фактов явлений, действий, правил;

6. мотивация учеников к первоначальному обобщению только что появившихся фактов, изучение учениками фактов, носящих словно не поддающийся объяснению характер и приведенные в истории науки к созданию научной проблемы;

7. создание связей между предметами [3, С. 114].

Выявим признаки проблемного обучения. Первая особенность — это особенная интеллектуальная активность ученика по самостоятельному изучению новых неизвестных понятий с помощью решения учебных проблем, которая дает глубину, сознательность, развития логико-теоретического и интуитивного мышления, прочность знаний.

Следующая особенность заключается в том, что проблемное обучение – самое продуктивное средство организации мировоззрения, так как создаются особенности творческого, критического, диалектического мышления в процессе проблемного обучения [15].

Третья особенность следует из закономерной взаимной связи между теоретическими проблемами и практическими проблемами и фиксируется дидактическим принципом взаимосвязи обучения с жизнью. При проблемном обучении связь с практикой и применение жизненного опыта учащихся считают причиной получения новых знаний и областью приложения усвоенных способов решения проблем. Связь с жизнью служит главным средством формирования проблемных ситуаций и критерием оценки верности решения учебных проблем.

Регулярное использование учителем различных видов и типов самостоятельной деятельности учеников, требующей как повторение ранее приобретенных, так и изучение новых неизвестных знаний и способов работы является четвертой особенностью проблемного обучения [15].

Дидактическим принципом индивидуального подхода, определенным присутствием учебных проблем различной сложности, воспринимаемые всяким учащимся неодинаково, этим определяется пятая особенность. Особое понимание проблемы создает различия выдвижения различных гипотез, в ее формулировании и нахождения каких-либо путей доказательства гипотез.

В подвижной связи элементов проблемного обучения состоит шестая особенность. Динамичность проблемного обучения заключается в переходе одной ситуации в другую естественным путем исходя из закона взаимной связи и обусловленности любых вещей и явлений окружающего нас мира.

В сильной эмоциональной деятельности учащихся, обусловленной проблемной ситуацией, которая является источником возбуждения, заключается седьмая особенность.

Восьмая особенность проблемного обучения состоит в обеспечении им новым соотношением индукции и дедукции и новая зависимость репродуктивного и продуктивного приобретения знаний.

Первая, вторая и третья особенности проблемного обучения носят социальный характер (гарантируют глубину убеждений, прочность знаний, способность творчески использовать знания в жизни). Оставшиеся особенности имеют специально-дидактический характер и в общем дают характеристику проблемному обучению.

Выделять виды проблемного обучения лучше по имещимся видам творчества. Согласно с отобранным основанием обозначим три вида проблемного обучения:

• научное творчество — теоретическое исследование, …означает поиск открытия учащимися нового закона, правила, доказательства; во главе данного вида проблемного обучения находится постановка и нахождение решения теоретических учебных проблем;

• практическое творчество — нахождение практического решения, а именно способа использования в новой ситуации известного знания, изобретение, конструирование; главное этого вида проблемного обучения состоит в постановке и решении практических учебных проблем;

• художественное творчество — художественное изображение действительности на основе творческого воображения, которое включает рисование, музицирование, игру и т. п. [15].

В большинстве случаев на теоретических занятиях применяется первый вид проблемного обучения, где организуется групповое, фронтальное или индивидуальное решение проблемы. Второй вид используется на практических занятиях, лабораторных, на предметном кружке, на производстве, на факультативе. На внеурочных и урочных занятиях применяется третий вид. Решением, в особенности, групповых или индивидуальных учебных проблем характеризуются второй и третий виды проблемного обучения.

Названные перед этим виды проблемного обучения могут иметь различные уровни, условно выделяемые в проблемном обучении.

Восприятие учениками разъяснений учителя, усвоение образца умственного действия в условиях проблемной ситуации, выполнение самостоятельных работ, заданий воспроизводящего характера – это уровень обычной несамостоятельной активности.

Уровень на половину самостоятельной активности описывается применением изученных знаний в неизвестной ситуации и участием учеников в общем с учителем нахождении способа решения данной учебной проблемы.

Проделывание самостоятельных работ репродуктивно-поискового типа, в котором ученик самостоятельно занимается по тексту учебника, использует изученные знания в новейшей ситуации, строит решение задачи среднего уровня сложности, с помощью логического анализа обосновывает гипотезы с небольшой помощью учителя, предусматривает уровень самостоятельной активности.

К уровень творческой активности относится проделывания самостоятельных работ, которые требуют творческое воображение, логический анализ, открытие нового неизвестного способа решения, доказательства без помощи кого-либо. На данном уровне строятся самостоятельные выводы и обобщения; художественное творчество имеет место здесь также.

Уровни проблемного обучения передают не только различный уровень изучения учениками новых знаний и способов умственной работы, а также различные уровни мышления. Перемещение учеников с первого на более высокий уровень есть результат проблемного обучения и вместе с тем процесс руководства их учебно-познавательной деятельностью [16].

Методы и виды проблемного обучения.

Можно выделить шесть дидактических способов создания процесса проблемного обучения, которые представляют собой три вида передачи учебного материала педагогом и три вида организации педагогом самостоятельной учебной деятельности обучающихся. Рассмотрим данные методы.

1. Метод монологического изложения

Применительно к математике он используется не так часто, так как изложение теоретических фактов чаще всего происходит в виде эвристической беседы, но в некоторых случаях монологическое изложение применить возможно. Его суть состоит в сообщении учителем фактов в нужной последовательности, далее дает им нужные пояснение, показывает практическими примерами с целью их применения. Например, при изложении нового материала по теме «Числовые последовательности». Применение технических средств обучения и средств наглядности вместе с разъясняющим текстом. Учитель раскрывает между явлениями и понятиями те связи, требующие для понимания данного материала, которые вводит их в порядке информации [4].

Проблемные ситуации создаются только для того чтобы привлечь внимание учеников.

Пример 1. Приводим несколько числовых последовательностей среди них арифметическая прогрессия, в результате появляется проблемная ситуация: как получить каждый последующий член в данной числовой последовательности?

Пример 2. 7 класс, формулы сокращенного умножения. На этапе актуализации перед изучением формулы разности квадратов дается такая ситуация:

Вычислить: .

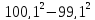Имеющихся знаний недостаточно для решения примера рациональным способом. Появляется проблемная ситуация – нахождение рационального способа.

После ее создания, ответа на вопрос «почему так, а не иначе?», от учащихся не нужен, тут же выдается фактический материала. Материал несущественно изменяется при применении монологического метода обучения. Педагог обычно только исправляет порядок следования сообщаемых фактов, демонстраций, опытов, показа средств наглядности и в качестве дополнительных элементов содержания использует интересные факты из истории развития изучаемого понятия или факты, повествующие о практическом применении усваиваемых знаний в науке и технике, для того чтобы создать проблемную ситуацию. Роль учащегося при применении этого метода достаточно пассивна, нужный для работы с этим методом уровень познавательной самостоятельности низок.

В данной организации процесса изучения нового знания педагог соблюдает все главные требования к уроку, реализуя дидактические принципы доступности изложения, наглядности, соблюдая точную последовательность в порядке следования информации, поддерживая крепкое внимание учеников к осваиваемой теме, тем не менее выбранный им метод обучения превращает учащегося в пассивного слушателя, не оживляет его познавательную работу [4]. Применяемый в данном случае метод обучения дает возможность достичь лишь одной цели - прибавить в запас знаний учеников дополнительные факты.

2. Рассуждающий метод обучения

Данный метод проблемного обучения применим, если перед учителем стоит цель представить образец исследования и решения некоторой целостной проблемы.

Например, к исследованию функции применение производной.

Материал делится на некоторые части, учитель на любом этапе предполагает системы риторических вопросов проблемного характера для того чтобы привлечь учеников к мыслительному анализу проблемных ситуаций. Способ преобразования материала для работы данным методом различается, главным образом тем, что в содержание в качестве вспомогательного структурного элемента внедряется система риторических вопросов. Порядок сообщаемых фактов таким образом выдается, чтобы беспристрастные противоречия содержания были показаны более выделено, выпукло, вызывали познавательный интерес учеников и готовность их разрешить.

В рассказе педагога доминирует уже не категоричность сведений, а основы рассуждения, нахождения выхода из появляющихся исходя из особенностей организации материала затруднений. Выбирая рассуждающий метод обучения, педагог в процессе построения процесса усвоения применяет объяснительным методом обучения, сущность которого состоит в включении в сообщения педагогом фактов данной науки, их характеристике и разъяснение, а именно показывает сущности новых неизвестных понятий при помощи наглядности, слова и практических действий [18].

3. Диалогический метод изложения

Данный метод проблемного обучении наиболее часто применим при изучении математики. Начиная с младших классов при выдачи нового материала, педагог выстраивает диалог, формулируя проблемные вопросы. Тем самым педагог устанавливает перед собой задачу: вовлечь учеников к прямому участию в осуществления способа решения проблемы. Цель - задействовать, поднять познавательный интерес, в новом материале привлечь внимание к уже известному.

Например, 6 класс, тема «Противоположные числа. Модуль числа».

Фрагмент урока:

Задание. На координатной прямой отметим точки А(5), В(-4). Найдем расстояние от начала отсчета до каждой из точки (таблица 2).

Таблица 2

Точка	Координата	Отрезок	Расстояние (в единичных отрезках)
А	5	ОА	5
В	-4	ОВ	4

Модулем числа b называют расстояние в единичных отрезках от начала отсчета до точки А(b).

Записывают: 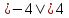; 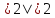, , 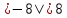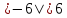. Читают: "Модуль числа 2 равен 2. Модуль числа -8 равен 8 и так далее ".

Задание. Покажите на координатной прямой модули чисел 7 и -7. Делаем вывод: ,

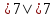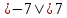
Число 7 – положительное, а его модуль?  (Модуль положительного числа равен самому этому числу, т.е. если b - положительное, то ).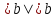

Число -7 – отрицательное, а его модуль? Какой вывод? (Модуль отрицательного числа равен числу без знака, т.е. если b - отрицательное, то ).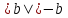

Чему же равен модуль нуля? 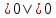. (Модуль нуля равен нулю.)

Задание. Допустим нам надо выйти из точки и пройти путь в 9 км (1км = 1 ед. отрезку). В какую точку мы попадём? Как нужно передвигаться для того чтобы оказаться в этих точках? (в противоположных направлениях)

Как вы считаете, как мы можем назвать данные числа? Таким образом, числа 9 и -9 будут противоположными. Какие числа мы можем называются противоположными, попытайтесь сформулировать определение данных чисел.

Определение: Два числа, отличающиеся друг от друга только знаками, называются противоположными.

Применение диалогического метода преподавания гарантирует наиболее высокий уровень познавательной деятельности учеников в процессе познания, потому что они уже собственно привлекаются к взаимодействию в решении проблемы под строгим управлением учителя.

4. Эвристический метод изложения

Эвристический метод используется в тех случаях, когда преподаватель устанавливает цель научить обучающихся некоторым элементам решения проблемы, сформировать не полный поиск новых знаний и способов действия. Применяя эвристический метод, педагог использует такую же организацию учебного материала, как при диалогическом методе, но немного пополняет его структуру формулировкой познавательных задач и заданий ученикам на любом некотором этапе решения учебной проблемы. Итак, формой организации данного метода является соединение эвристической беседы с решением проблемных задач и заданий [4].

Сущность эвристического метода заключается в открытие нового правила, закона, теоремы и т.д. не преподавателем при участии учеников, а самими учениками под управлением и при помощи преподавателя.

Например, геометрия 8 класс, тема «Теорема Пифагора»

Фрагмент урока:

На актуализации вспоминают свойства квадрата, прямоугольника, различных треугольников, даются задания для нахождения площадей и сторон фигур. Далее дается следующая задача:

В прямоугольном треугольнике (рисунок 2) катет 4 см и гипотенуза - 5 см.

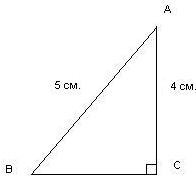
Рисунок 2

Найти площадь треугольника АВС.

Вычислить площадь невозможно.

Почему нельзя? – Катет ВС не известен.

В данной задаче на какие вопросы должны дать ответ?

Вычислить катет ВС и .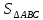

Возможно ли дорешать задачу? Почему? – Нет. Не хватает знаний.

(Задачи выбраны так, чтобы ситуация успеха поменялась проблемой. Как будем находить стороны прямоугольного треугольника? Обратить внимание на значение слова “зависимость”.)

Какую мы можем поставить для себя задачу? – Как найти гипотенузу и катет в прямоугольном треугольнике?

Стало быть, какая может быть зависимость между гипотенузой и катетами в прямоугольном треугольнике?

Догадаетесь или нет, если я вам предложу прямоугольный треугольник со сторонами 3, 4 и 5,  какая зависимость между данными сторонами?

25 = 9+16?

16= 9+25?

9= 16+25?

А есть ли такая же зависимость в данном треугольнике (рисунок 3)?

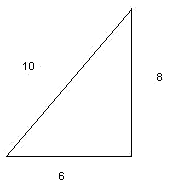
Рисунок 3

Да, 100 = 36+64

Давайте произнесем на языке геометрии, какая зависимость у нас получилась? – Квадрат гипотенузы равен сумме квадратов катетов.

Но данных похожих чисел большое количество! Поэтому, какую мы выдвигаем гипотезу? – В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

А можно ли данную зависимость использовать при решении задач? Для любых ли прямоугольных треугольников мы можем использовать данную зависимость? Мы не знаем! Надо это доказать! Давайте сформулируем эту теорему.

Теорема: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано:

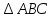
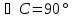
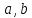– катеты

с – гипотенуза

Доказать:

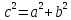
Доказательство:

Доказывается по аналогии с теоремой о площади прямоугольника. Достроим треугольник до квадрата со стороной 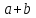(рисунок 4).

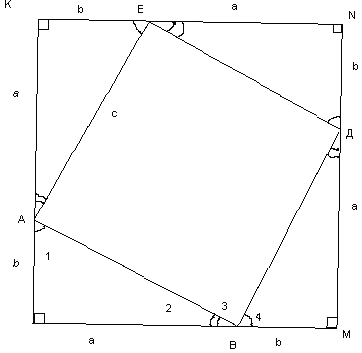
Рисунок 4

Что мы можем найти? – Площадь квадрата.

Чему равна площадь квадрата CMNK? – Квадрату его стороны, то есть 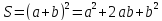(1).

Давайте соединим концы этих отрезков. Обозначим буквами данные точки АВДЕ. Подпишем и обозначим стороны образовавшихся фигур на чертеже. Равны ли получившиеся треугольники? – Да. По двум катетам!

Обозначим углы данных треугольников. Напротив равных сторон лежат равные углы. Что поучилось с квадратом? – Он разделен на четыре треугольника и четырехугольник ДВЕА.

Каким еще способом можно найти площадь квадрата? – По второму свойству: , .

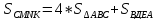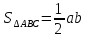Как вычислить 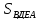? Что нужно знать? Какой это четырехугольник? – Стороны равны с.

Это квадрат? Мы же знаем, нельзя верить глазам своим, если идет речь о геометрии. Поэтому определение вида данного четырехугольника на глаз не подходит. Следовательно, нужно доказать! Давайте определим 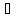В!

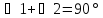(по свойству острых углов);

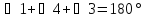(составляет развернутый угол);

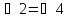(из равенства треугольников);

;

;

;

.

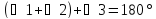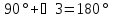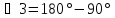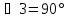Точно так же можно доказать, что остальные углы равны 90°. Из этого какой можно сделать вывод? – Четырехугольник ВДЕА – квадрат со стороной а.

Чему будет равна 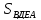? – Квадрату его стороны!

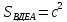
Вернемся к площади квадрата CMNK.

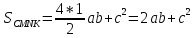(2).

Обратим внимание на равенства (1) и (2). Что вы видите? – Левые части равенств равны.

Какой из этого можем сделать вывод? – Правые тоже равны, то есть

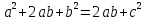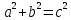, или.

Следовательно, мы взяли произвольный прямоугольный треугольник со сторонами а, b и с и доказали, что? – В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

5. Исследовательский метод

Педагог строит методическую систему проблем и проблемных задач, подстраивает ее к нужной ситуации учебного процесса, предъявляет ученикам, таким образом контролируя их учебную деятельность. [14].

На уроке с использованием исследовательского метода берутся элементы структуры эвристического метода, порядок следования вопросов, указаний, заданий. Но в процессе реализации эвристического метода эти вопросы, указания и задания носят предварительный характер, а именно задаются до решения подпроблемы. Когда применяется исследовательский метод, вопросы задаются в конце этапа, после того как большая часть учеников справились с решением подпроблемы.

Данный метод применяется чаще всего в старших классах, при котором учащиеся исследуют проблему самостоятельно.

Например, геометрия, 7 класс, тема: «Теорема о сумме углов треугольника»

Преподаватель называет тему урока и выдает задание ученикам:

Начертить треугольник по заданным углам:

1. 

2. 

3. 

Ученики пробуют построить треугольники, но это сделать у них не получается. Во всех случаях не выполняется условие о сумме внутренних углов треугольника. Поэтому, формируется проблемная ситуация:

• зависит ли сумма внутренних углов треугольника от его размеров, формы, положения на плоскости?

• выдается задание: начертить два треугольника, с помощью транспортира измерить внутренние углы и вычислить их сумму.

Формулируется гипотеза: сумма внутренних углов треугольника равна 180°, далее доказывается соответствующая ей теорема.

6. Метод программированных заданий

Метод программированных заданий состоит из постановки преподавателем системы программированных заданий, которая состоит в следующем: все задания состоят из отдельных элементов-кадров; в одном кадре содержится часть осваиваемого материала, который сформулирован в виде вопросов и ответов, или в виде представления новых заданий, или в виде упражнений.