Вопрос16.

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Для независимых X и Y

М(XY)=MX MY(без док-ва)

Характеристика разброса X-МХ – отклонение

Чтобы убрать “-“ возведём в квадрат

DX=M(X-MX)^2 – средний квадрат отклонения называется дисперсия.

Раскроем скопки:

DX=M(x^2-3x*MX+(MX)^2)= MX – const  M(MX)=MX

=M(x^2-2MX*MX+(MX)^2)=M(x^2)-2(MX)^2+(MX)^2=-M(x^2)-(MX)^2

Где M(x^2)=x1^2*P1+x2^2*P2+…xn^2*Pn или M(x^2)= x^2f(x)dx

Свойства дисперсии:

1) D(C)=0; C-const

2) D(C X)=C^2*D(X), C-const

3) D(X+Y)=D(X)+D(Y), если X,Y – независимые случайные величины

Вопрос 17.

Биномиальное распределение (дискретное)

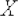 - количество «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна  .  .

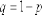Закон распределения   имеет вид:

Закон распределения   имеет вид:

	0	1	…..	k	…..

Здесь вероятности находятся по формуле Бернулли:  .

Характеристики:  ,  , 

Примеры многоугольников распределения для   и различных вероятностей:

Пуассоновское распределение (дискретное)

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии 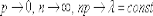 закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность   события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

	0	1	…..	k	…..
			…..		…..

Вероятности вычисляются по формуле Пуассона:  .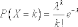

Числовые характеристики:  ,  , 

Разные многоугольники распределения при  .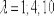

Среднеквадратическое отклонение -  наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.

 Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

Среднее квадратическое отклонение σ(Х) с.в. Х: σ(Х)=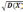

Вопрос 18.

Биномиальное распределение (дискретное)

 - количество «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна  .  .

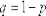Закон распределения   имеет вид:

Закон распределения   имеет вид:

	0	1	…..	k	…..

Здесь вероятности находятся по формуле Бернулли:  .

Характеристики:  ,  ,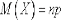 

Примеры многоугольников распределения для   и различных вероятностей:

Пуассоновское распределение (дискретное)

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии  закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность   события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

	0	1	…..	k	…..
			…..		…..

Вероятности вычисляются по формуле Пуассона:  .

Числовые характеристики:  ,  , 

Разные многоугольники распределения при  .

Локальная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

 где   - функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Свойства функции ϕ(x):

1. ϕ (x) > 0

2. ϕ (− x)= ϕ (x)

3. limx ϕ (x)=0, (ϕ (ϕ )<10 ^-4

Интегральная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2)

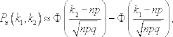 где  - функция Лапласа

Свойства функции Лапласа:

1. Ф(−х) =Ф(х)