Вопрос 14.

Функция  - производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины .

Следовательно, функция распределения F(x) выражается через плотность распределения:

В ероятность того, что непрерывная случайная величина X примет значение, принадлежащие интервалу (a, b) равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:

График 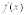называют также законом распределения или кривой распределения.

Укажем основные свойства плотности распределения.

1.  Плотность распределения есть неотрицательная функция:

.

Это свойство непосредственно вытекает  из того, что функция распределения  есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

.

Это следует из формулы и из того, что .

Геометрически основные свойства плотности распределения означают, что:

1) вся кривая распределения лежит не ниже оси абсцисс;

2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения , как всякая вероятность, есть величина безразмерная. Размерность плотности распределения , обратна размерности случайной величины.

Пример:

Вопрос 15.

Математическое ожидание и его свойства.

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности. Т.е., если сл. величина имеет закон распределения, то

называется её математическим ожиданием. Если сл. величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда , при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание не существует).

Для непрерывной сл. величины, заданной функцией плотности вероят­ности f(x), математическое ожидание определяется в виде интеграла

при условии, что этот интеграл существует (если интеграл расходится, то говорят, что математическое ожидание не существует).

Свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной равно самой этой постоянной. Постоянная С принимает это значение с вероятностью единица и по определению М(С)=С×1=С

Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.Ограничимся доказательством этого свойства только для суммы двух дискретных случайных величин, т.е. докажем, что

Под суммой двух дискретных сл. Величин понимается сл. Величина, которая принимает значения  с вероятностями По определению

Но

где  вероятность события , вычисленная при условии, что . В правой части последнего равенства перечислены все случаи появления события , поэтому  равна полной вероятности появления события , т.е. . Аналогично . Окончательно имеем

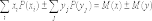
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

У				…
Q				…
Х				…
Р				…

 

 

 

 

 

Приведем доказательства этого свойства только для дискретных величин. Для непрерывных случайных величин оно доказывается аналогично. Пусть Х и У независимы и имеют законы распределения Произведением этих случайных величин будет случайная величина, которая принимает значения  с вероятностями равными, в силу независимости случайных величин, . Тогда

Следствие. Постоянный множитель можно выносить за знак матема­тического ожидания. Так век постоянная С не зависит от того какое значение примет сл. величина X, то по   свойству 3. Имеем М(СХ)=М(С)×М(Х)=С×М(Х)