Вопрос 10.

Последовательности независымых испытаний. Схемы Бернулли. Формулы Бернулли(вывод). Условия применения формулы Бернулли.

Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли:

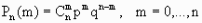
Вероятность Р_n(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m₀, а затем уменьшается при изменении m от m₀до n. Поэтому m₀, называют наивероятнейшим числом наступлений успеха в опытах. Это число m₀, заключено между числами np-q и np+p (или, что тоже самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p. Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.

Вопрос 11.

Центральная предельная теорема теории вероятностей. Теорема Муавра-Лапласа.

Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым.

Пусть  последовательность одинаково распре­делённых случайных величин с математическими ожиданиями  и дисперсиями .

ТЕОРЕМА. Если случайные величины  независимы и , то при достаточно большом n закон распределения суммы 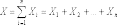 будет сколь угодно близок к нормальному закону распределения .

Так как в условиях теоремы случайные величины независимы, то

т.е. в условиях теоремы сумма  имеет закон распределения близкий к .Так' как  na и  с ростом п, возрастают, то удобнее рассматривать не просто суммы , а нормированные суммы . Такие суммы при  имеют закон распределения .

Интегральная теорема Лапласа. Пусть X есть число наступлений собы­тия в п независимых опытах, в каждом из которых вероятность появления события равна .Тогда при достаточно больших n вероятность того, что событие появится от  до  раз равна

, где q=1-p, Ф(х) – функция Лапласа.

Эта теорема является следствием из, центральной предельной теоремы, хотя и была доказана гораздо раньше неё. В самом деле, число появлений события в n независимых опытах можно представить следующим образом

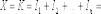число успехов,

где  - число появлений события в i -м опыте, причём ранее было показано, что  и . Т.е. X является суммой большого числа независимых случайных величин  и . Условия центральной предельной теоремы выполнены, X имеет закон распределения близкий к

Если для этого закона распределения записать с помощью формулы (**) вероятность попадания случайной величины в интервал , то и получится утверждение теоремы (Муавра-Лапласа).

Пример 1. Вероятность выпуска изделия второго сорта равна 0,2. Изделия отправляют партиями по 100 штук. Какова вероятность того, что во взятой наугад партии содержится от 20 до 25 изделий второго сорта?

Имеем n=100, р=0.2, q=0.8