Вопрос 8.

Полная группа событий, понятия. Теорема о полной вероятности. Привести примеры. 1)Теорема. Сумма вероятностей событий А₁ , А₂ , ..., А_n , образующих полную группу, равна единице:

Р (A₁) + Р (А₂) + ... + Р (А_n) = 1.

Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то

Р (A₁ + A₂ + ... + A_n) = 1.     (*)

Любые два события полной группы несовместны, поэтому можно применить теорему сложения:

Р (А₁ + А₂ + ... + А_n) = Р (A₁) + Р (A₂) + ... + Р (А_n).    (**)

Сравнивая (*) и (**), получим

Р (А₁) + Р (А₂) + ... + Р (А_n) = 1.

Пример 1. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.

Р е ш е н и е. События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность

q = 1 — p = 1 — 0,7 = 0,3,

2) Пусть требуется определить вероятность некоторого события  , которое может произойти вместе с одним из событий:

,

образующих полную группу несовместных событий. Будем эти события называть гипотезами.

Докажем, что в этом случае

,           

т.е. вероятность события   вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Формула (3.4.1) носит название формулы полной вероятности.

Доказательство. Так как гипотезы   образуют полную группу, то событие   может появиться только в комбинации с какой-либо из этих гипотез:

.

Так как гипотезы   несовместны, то и комбинации 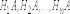  также несовместны; применяя к ним теорему сложения, получим:

.

Применяя к событию   теорему умножения, получим:

,

что и требовалось доказать.

Пример 1. Имеются три одинаковые на вид урны; в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.

Решение. Рассмотрим три гипотезы:

 - выбор первой урны,

- выбор второй урны,

 - выбор третьей урны

и событие   – появление белого шара.

Так как гипотезы, по условию задачи, равновозможные, то

.

Условные вероятности события   при этих гипотезах соответственно равны:

.

По формуле полной вероятности

.

Вопрос 9.

Полная группа событий, понятия. Какие событиями называются гипотезами? Вероятности гипотезы(формулы Байеса). Примеры. Теорема. Сумма вероятностей событий А₁ , А₂ , ..., А_n , образующих полную группу, равна единице:

Р (A₁) + Р (А₂) + ... + Р (А_n) = 1.

Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то

Р (A₁ + A₂ + ... + A_n) = 1.     (*)

Любые два события полной группы несовместны, поэтому можно применить теорему сложения:

Р (А₁ + А₂ + ... + А_n) = Р (A₁) + Р (A₂) + ... + Р (А_n).    (**)

Сравнивая (*) и (**), получим

Р (А₁) + Р (А₂) + ... + Р (А_n) = 1.

Пример 1. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.

Р е ш е н и е. События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность

q = 1 — p = 1 — 0,7 = 0,3,

2) Рассмотрим вероятность события А, которое может наступить при условии появления одного из попарно независимых событий  ,  , …, , 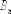образующих полную группу. События  ,  , …,  в этом случае называются гипотезами.

3) Пусть событие   происходит одновременно с одним из   несовместных событий  . Требуется найти вероятность события  , если известно, что событие   произошло.

На основании теоремы о вероятности произведения двух событий можно написать

Откуда

или

Формула формулы Байеса.

Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.

Решение. Пусть   — события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут

, ,

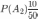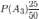
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

По формуле Байеса находим исходную вероятность

.