Вопрос 40.

Критерий Романовского, его сущность и применение.

Критерий Романовского с основан на использовании критерия Пирсона, т.е. уже найденных значений , и числа степеней свободы df:

c=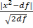

Он удобен при отсутствии таблиц для . Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

Вопрос 41.

Характеристическая функция случайной величины, ее свойства.

Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид.

CB x - матем. ожидание СВ 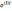, где , t-произвольное действ. число:

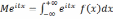, где Х - непрерыв СВ с плотностью f(x).

С помощью характерист. фун-ии можно определить начальные моменты C,B,X. Если начальный мом. к-го порядка конечен, то M( )= 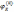(0) Отсюда следует, что M(x)=-i , D(x)=- (0)+( (0)

(t)=M( )= f(x)dx, f(x)-x- плотность распр. х. -∞ i= . Интеграл правой части(1) зависит от параметра t, диф-ия рав-то по t,

(t)= f(x)dx=i f(x)dx.

(t)= f(x)dx... (t)= = M( )= . В частности: (0)=i =

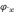i M(x)= M(x)= ( (o) =- (0)+( (0) .

Замечание = .

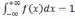Вопрос 42.

Случайные функции, их характеристики и свойства.

Математическое ожидание случайной функции   определяется следующим образом. Рассмотрим сечение случайной функции   при фиксированном  . В этом сечении мы имеем обычную случайную величину; определим ее математическое ожидание. Очевидно, в общем случае оно зависит от  , т. е. представляет собой некоторую функцию  :

.

Таким образом, математическим ожиданием случайной функции   называется неслучайная функция  , которая при каждом значении аргумента   равна математическому ожиданию соответствующего сечения случайной функции.

Аналогичным образом определяется дисперсия случайной функции.

Дисперсией случайной функции   называется неслучайная функция  , значение которой для каждого   равно дисперсии соответствующего сечения случайной функции:

.  

Дисперсия случайной функции при каждом   характеризует разброс возможных реализаций случайной функции относительно среднего, иными словами, «степень случайности» случайной функции.

Очевидно,   есть неотрицательная функция. Извлекая из нее квадратный корень, получим функцию   - среднее квадратическое отклонение случайной функции:

. 

Функция распределения случайной величины. Её свойства

Каждая случайная величина полностью определяется своей функцией распределения.

Если  .- случайная величина, то функция F(x) = F_ (x) = P( < x) называется функцией распределения случайной величины  . Здесь P( < x) - вероятность того, что случайная величина  принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• F(x) определена на всей числовой прямой R;

• F(x) не убывает, т.е. если x₁ x₂, то F(x₁)  F(x₂);

• F(- )=0, F(+ )=1, т.е.   и  ;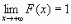

• F(x) непрерывна справа, т.е. 

Функция распределения дискретной случайной величины

Если  - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …

Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_ (x) непрерывна, то случайная величина  называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_ (x), которая связана с функцией распределения F_ (x) формулами

 и  .

Отсюда, в частности, следует, что для любой случайной величины  .