Вопрос 30.

Статистический ряд, этапы его обработки. Эмпирический закон распределения для дискретной и непрерывной случайных величин.

Статистический ряд – перечень вариантов и соответствующих им частот или относительных частот.

Обработка: Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной , оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюденных значений на интервалы или «разряды» и подсчитаем количество значений ni, приходящееся на каждый i - й разряд. Это число разделим на общее число наблюдений n и найдем частоту, соответствующую данному разряду: ni /n = Wi

Сумма частот всех разрядов, очевидно, должна быть равна единице.

Эта таблица называется статистическим рядом:

Xi	X1	X2	X3	X4	…	Xi
Wi	W1	W2	W3	W4	…	Wi

Эмпирическая функция распределения (для дискретной величины) – функция F(х)=nх /n, определяющая для каждого x относительную частоту событий Х < x;

где nх – число выборочных значений, меньших Х; n – объём выборки.

Эмпирическая функция распределения (для непрерывной случайной величины)

Эмпирическая функция непрерывна справа

F(х)=

– скачки функции F(х)

Вопрос 31.

Точечные оценки параметров распределения. Требования несмещённости и состоятельности оценки. Привести примеры смещённой и несмещённой оценок параметров.

Точечной оценкой параметра распределения θ называют некоторую функцию результатов наблюдений, значения которой близки к неизвестной характеристике θ генеральной совокупности.

Для построения оценки нужны критерии, по которым судят о её качестве:

1. Оценка 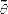называется несмещенной, если её математическое ожидание равно оцениваемой характеристике случайной величины:

т. е. если она не дает систематической ошибки.

2. Оценка называется состоятельной, если при увеличении числа наблюдений оценка сходится по вероятности к искомой величине, т. е. для любого сколь угодно малого

Если известно, что оценка несмещенная, то для проверки состоятельности её удобно пользоваться условием: .

Если последнее условие выполнено, то из неравенства Чебышева следует, что оценка состоятельная. .

Иными словами, состоятельность означает, что оценка, построенная по большому числу наблюдений, имеет меньший разброс (дисперсию), т. е. .

Примеры смещённой и несмещённой оценок параметров:

Оценка математического ожидания

Пусть имеется случайная величина Х с математическим ожиданием m и дисперсией D, при этом оба эти параметра неизвестны. Над величиной Х произведено N независимых экспериментов, в результате которых была получена совокупность N численных результатов x1, x2, …, xN. В качестве оценки математического ожидания естественно предложить среднее арифметическое наблюдаемых значений

М(х)= – Оценка математического ожидания является несмещенной.