7.3Оптимальний прийом дискретних сигналів

Виведемо співвідношення по якому радіоприймач правдоподібно вибере сигнал

Джерело дискретних повідомлень характеризується сукупністю можливих повідомлень U₁, U₂, … , U_n та відповідних ймовірностей їх появи

р(U₁), р (U₂) ,…, р (U_n).

В передаючому пристрої каналу γ повідомлень ставиться у відповідність сигнал S₁… S_n , при чому ймовірність їх появи

р (S₁) р (U₁), і т.д. р (U_n) р (S_n).

В процесі передачі на сигнал накладається завада . Нехай дана завада має рівномірний спектр потужності .

Тоді , для адитивної завади маємо

х(t) = S_i(t) + W(t) i = 1… n .

Так як сигнали дискретні , то вони скінченні по часу , тобто тривають на інтервалі 0 < t < T, а раз так , то їх можна розкласти в ряди

S i(t) = , де — артарирмований базис функцій

Аналогічно

W(t) = (1)

х(t) =

Причому х_l = S_il + W_l , де

S_il = dt

W_l = dt

Оскільки завада має нормальний розподіл з нульовим середнім значенням та дисперсією

то її функція розподілу

(2)

Зрозуміло, що х_l ,буде мати такий же розподіл з такою ж дисперсією, але середнім значенням рівним S_il , тобто

Так як окремі значення завади не залежать один від одного (поза рамками взаємної часової кореляції) , то умовний розподіл

представиться добутком однорідних розподілів:

Аналогічно можна записати умовний розподіл ймовірності , отримати сигнал х при відправленому сигналі S_j (помилкове рішення)

Тоді умова оптимального прийому Котельникова

= >

Якщо про логарифмувати останнє співвідношення отримаємо

*

— < No ln

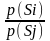
Ясно що

х(t) – S_i(t) =

Тоді після піднесення в квадрат і інтегрування, з врахуванням ортонормованості функцій отримаємо

dt =

тоді (_*) буде мати вигляд

- , i j

Дана нерівність може використовуватись для визначення правильного приймання сигналу S_i(t). Якщо ймовірності усіх сигналів алфавіту “n” рівномірні, тобто

р (S₁) = р(S₂) = …= р(S_n) =

то критерій Котельникова набуде виду

*

*

, i j .

ε_i² ε_j²

Звідси висновок, що при правильному прийомі сигналу оптимальний приймач видасть повідомлення , яке відповідає переданому сигналу, який має менше середньоквадратичне відхилення від прийнятого сигналу.

Нерівність (_*) (_*) можна переписати по іншому. Якщо підняти в квадрат і розбити на суму інтегралів , то для рівних по енергії сигналів , коли

dt dt E_s , матимемо

(!)

Тобто умова оптимального прийому буде наступною :

Якщо енергії усіх сигналів однакові, та ймовірності появи їх теж однакові, то оптимальний приймач відтворить повідомлення , яке відповідає тому переданому сигналу , взаємна кореляція якого з прийнятим сигналом максимальна.

Для двійкової системи (наявності двох сигналів) критерію Котельникова можна дати досить просту геометричну інтерпретацію.

Нехай передається повідомлення U₁ i U_{2 ,} і сформовані сигнали S₁(t) та S₂(t) . В “n” мірному просторі їм відповідають два вектори

Я сно , що прийнятому сигналу x при відправленому S₁ та заваді W₁. Простір можливих значень сигналу можна розбити на дві області так, щоб попадання в ліву область відтворювався сигнал S₁ а вправу S₂. Ясно, що коли „x” при сигналі S₁ попадає в область сигналу S₂ то відбувається помилка. Імовірність помилки залежить від конфігурації зон сигналів.

В оптимальному приймачі Котельникова простір сигналів розбивається так , щоб повна ймовірність помилок була найменша . При рівноймовірних сигналах і завади з рівномірним розподілом спектру потужності .

Оптимальним розбиттям буде таке, коли відтворюється та точка, той сигнал, до якого ближче знаходиться кінець вектора х.

Ясно , що в двомірному випадку це буде півплощина , яка в гіперпросторі перпендикулярна до вектора різниці S₁ – S₂ та йому перпендикулярна лінія (ОО’).

Якщо, наприклад, передавався сигнал S, а при заваді W прийняли сигнал x ближчий до то буде помилка коли тобто

|| x-S₂ || ² < || х-S₁ || ² або ж в евклідовій матриці:

,

що співпадає з умовою невірного прийому .

Структурна схема оптимального прийому :

Ц е є схема оптимального приймача Котельникова.

Якщо розкрити дужки то

,

при цьому його структурна схема

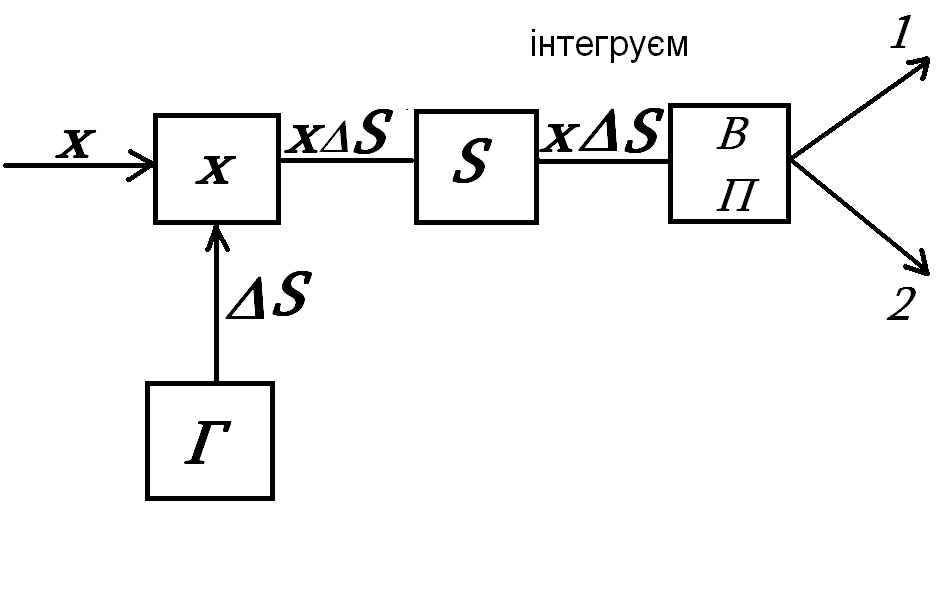
Як бачимо , вирішуючий пристрій t пороговий. Це схема простіша, але необхідно безперервно аналізувати сигнал по рівням.