7.2Оптимальне приймання сигналів

7.2.1.Критерій оптимальності

Поняття оптимального ( найкращого ) можна розглядати тільки в тому випадку , якщо умовитися , який зміст укладається в слово „оптимальність” . Для цього в кожному окремому випадку вводиться критерій оптимальності -

ознака за якою проводиться оцінка того чи іншого фізичного процесу , як найкращого ( оптимального ).

Вибір критерію оптимальності не є універсальним, він залежить від поставленої задачі та умов роботи.

Різноманітними критеріями оптимальності користуються не тільки в теорії приймання сигналів , а й у різних галузях науки та техніки, у повсякденному житті. Без чітко визначеного критерію оптимальність не має сенсу.

При передаванні дискретних сигналів широко застосовується критерій ідеального спостерігача , який вперше введено академіком В.О, Котельниковим у 1946 р. Тому досить часто цей критерій називають критерієм Котельникова. Згідно із цим критерієм приймач вважається оптимальним, якщо він забезпечує мінімум середньої ймовірності помилки .

При передаванні дискретних первинних сигналів b_i середня ймовірність помилки р_пом обчислюється як математичне сподівання ймовірності помилки кожного з них :

Р_пом = М [P_пом(b_i)] = 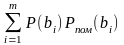, де

P(b_i) – імовірність передавання сигналу b_i ;

m – загальне число первинних сигналів.

Тоді критерій Котельникова ( ідеального спостерігача ) записується у вигляді:

min Р_пом = min

При передачі дискретних сигналів критерій Котельникова працює наступним чином :

Рахується що передаємо сигнал 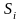, отримано сигнал х, тоді коли ймовірність

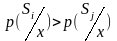, i j (1)

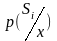– функція правдоподібності.

На основі формули Бейсса

Тоді нерівність (2) буде

(3)

або ж (4)

Відношення Λ – називають критерієм правдоподібності. Якщо всі сигнали рівноймовірні тобто

де m – об'єм алфавіту, то критерій Котельникова буде

Λ > 1 (5)

Незважаючи на натуральність та простоту, критерій Котельникова має недолік, який полягає в тому, що будь – які помилки вважаються однаково небажаними. У деяких випадках це допущення не є раціональним . Наприклад, при передаванні чисел помилка в перших ( старших ) розрядах більш шкідлива, ніж помилка в інших ( молодших ) розрядах . У цьому випадку застосовуються такі критерії оптимальності , які враховують міру небажаності тієї чи іншої помилки .

Ці втрати можна врахувати з допомогою вагових коефіцієнтів. Визначимо коефіцієнт втрат при неправильному прийомі сигнала L₁₂ та L₂₁ . L₁₂ (передали „ ” а прийняли „ ” ) . Тоді можна визначити середні передбачувані втрати

r = L₁₂ p_I + L₂₁ p_II

L₁₂ p_I - замість прийняти '

L₂₁ p_II - замість прийняти '

Оптимальним критерієм в даному випадку є система з найменшим середнім ризиком . В радіолокації широко використовують критерії Неймана– Пірсона . В даному критерії рахують :

1. Що помилкова тривога та пропуск цілі не є рівноцінними по наслідках.

2. Невідома апріорна імовірність сигналу , що передається .

Згідно критерію Неймана – Пірсона приймач є оптимальний , якщо при заданому значенні ймовірності помилковий тривоги

р_{пом.тривоги} = dx = β

він забезпечує найбільшу ймовірність правильного виявлення об’єкту

р _{виявлення} = 1- р_гр = 1 - dx

Можна показати , що критерій Неймана – Пірсона приводить до слідчого правила.

Λ =

де - деяке число , що виражається імовірністю помилкової тривоги.