2.3.1.Фізична суть спектральної густини амплітуд.

Якщо порівняти дискретні розклади в ряд Фур’є та інтегральний розклад то можна помітити що:

.- дискретне представлення - нова змінна

- неперервне представлення.

Можна замітити що при , верхній вираз переходить в нижній. Легко замітити, що:

Отже являється обвідною спектру дискретних частот, схожа на неї формою але дещо відрізняється норміровкою.

Для чого необхідно знати спектральний склад сигналу?

Якщо знати спектр сигналу можна за відомо розробити приймачі, які будуть пропускати лише дану смугу в каналі зв’язку. Дійсно такий спектр сигналу знаходимо в смузі частоти .

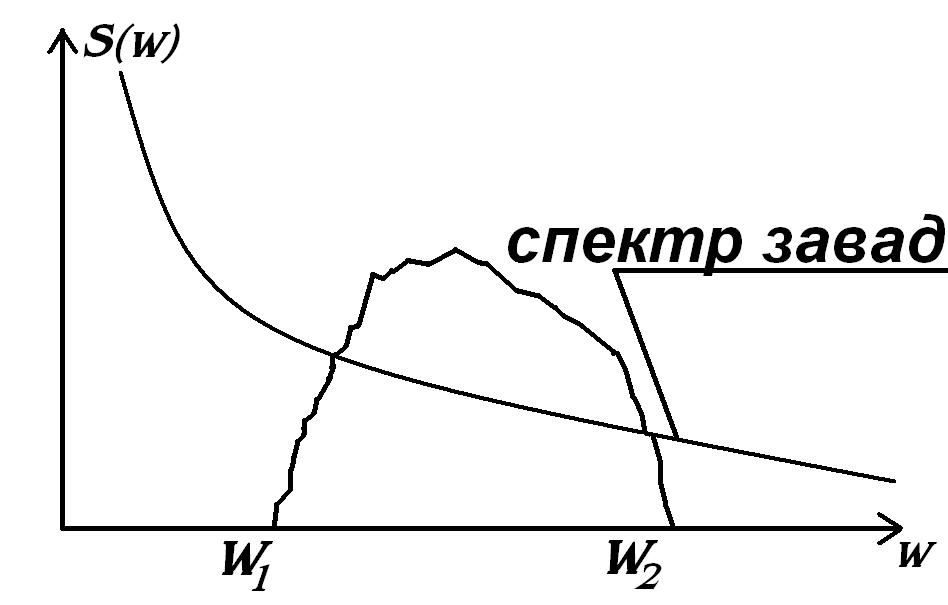
Тоді з врахуванням смуги пропускання, отримаємо відношення, що буде значно більшим ніж у випадку відсутності обмеження приймального тракту по частоті!!!

Знання спектрів дозволяє побудувати багатоканальні системи зв'язку з частотним розділенням сигналу.

Отже спектр сигналу необхідно знати для:

1. розділення інформаційних потоків, при побудові багатоканальних систем зв'язку.

2. для зменшення взаємного впливу інформаційних потоків.

3. для послаблення завад.

Представлення сигналу у виді сукупності гармонік являється доцільним, оскільки апаратна система каналів зв’язку може бути настроєна на приймання тієї чи іншої гармоніки.

Однак це не означає що існують якісь додаткові переваги ряду Фур’є перед іншими базами.

5. Фізична суть теореми Котельникова. Практичне використання теореми Котельникова.

Як вже відмічалось при передачі електричних сигналів завади можуть

змінювати сигнал. Відновити початковий сигнал значно простіше у тому

випадку якщо він дискретний.

Більше того, зовсім немає необхідності відновлювати все, за виключенням початкового сигналу, а досить відновити його в дискретні сукупності точок. Але весь сигнал при цьому починає втрачати інформацію. Тому виникає питання, яким чином привести дискретизацію сигналу без втрати його основної інформаційної частини?

Відповідь на питання дає теорема О.В.Котельникова.

Будь - який неперервний сигнал U(t), що не має частот, вищих за , можна точно відновити за його відліками , взятих з кроком дискретизації

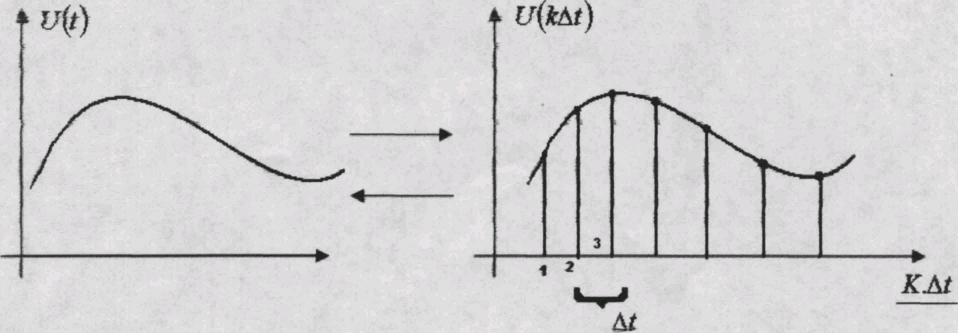
однозначне повернення

Доведення теореми.

Отже замість функції U(t) розглядається функція , яка повинна мати

такий же спектр як і U(t).

Нехай функція U(t) має обмежений спектр частотою . Тоді:

(1)

Отже наша функція (до речі парна по ) задана на інтервалі Розкладемо її в ряд Фур'є: (2)

це дійсно так. Періодом функції є

Вивід (2)

=

Розрахуємо коефіцієнти розкладу:

(3)

Тепер вернемось до функції U(t).

Застосуємо її спектральне представлення

(4)

Розглянемо дискретизовану функцію

(5)

Порівняємо вирази (3) та (5).

(6)

Отже (7)

Якщо ввести рівень дискретизації відмітимо, що парна функція відносно k.

(8) тоді спектральна густина

(9)

Так як спектральна густина однозначно визначає сигнал U(t), а сама може бути однозначно визначена по неперервній U(t) дискретній функції , де це доводить теорему. Отже для побудови функції U(t), що має обмежені частоти f<F необхідно і достатньо мати сукупність значень дискретизованої функції з кроком дискретизації . Далі приводиться розрахунок спектральної густини:

а далі відновлюється вся функція.

тут вже час не дискретизований!

Теорема Котельникова стверджує, що коли необхідно передати сигнал з обмеженим спектром F то достатньо передати його значення в точках відліку ; На приймальному кінці існує можливість повного відновлення .

Для практичного застосування теореми Котельникова необхідно вказати реальні пристрої відновлення по . Спосіб дискретного зняття інформації відносно простий. Його здійснюють шляхом замикання кола в певні моменти часу. Слід відмітити, що при цьому час релаксації вимірюючих приладів повинен бути надзвичайно малим, інакше будуть передаватись, не , а перехідні функції приладів!

На приймальному кінці пристрої, що відновлюють повинні реалізувати зв'язок між та рядами Котельникова.

Загальна структура пристрою: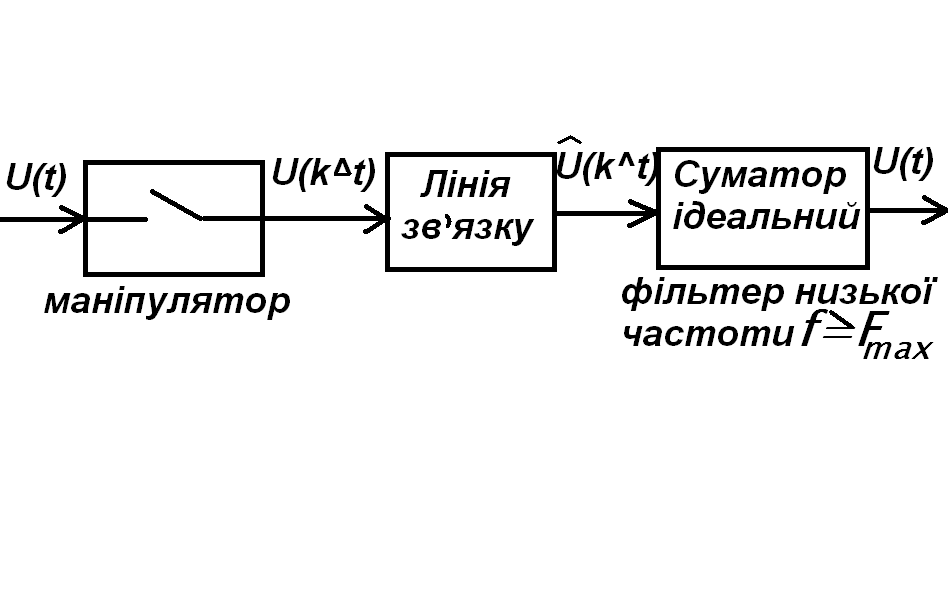

Обмеження теореми Котельникова для реальних сигналів передачі:

1. підлягають лише сигнали з

2. для реалізації необхідні маніпулятори, що мають дуже малі часи релаксації;

3. необхідні ідеальні фільтри низьких частот.

Оскільки реальні сигнали мають необмежений спектр, а функція відліків встановлена для строго обмежених спектрів то фільтр НЧ необхідно брати дещо ширшої смуги на 10 - 15%. Наприклад, якщо частота сигналу обмежена Гц то в системах з імпульсними способами передачі інформації її слід передавати з частотою 6800Гц. Фільтри НЧ і частота роботи вибирається 8000 Гц.