2.1.4.Дискретні.

Дискретними сигналами є сигнали, які характеризуються квантованими значеннями амплітуди, або ж існують в певні моменти часу (дискретні по часу).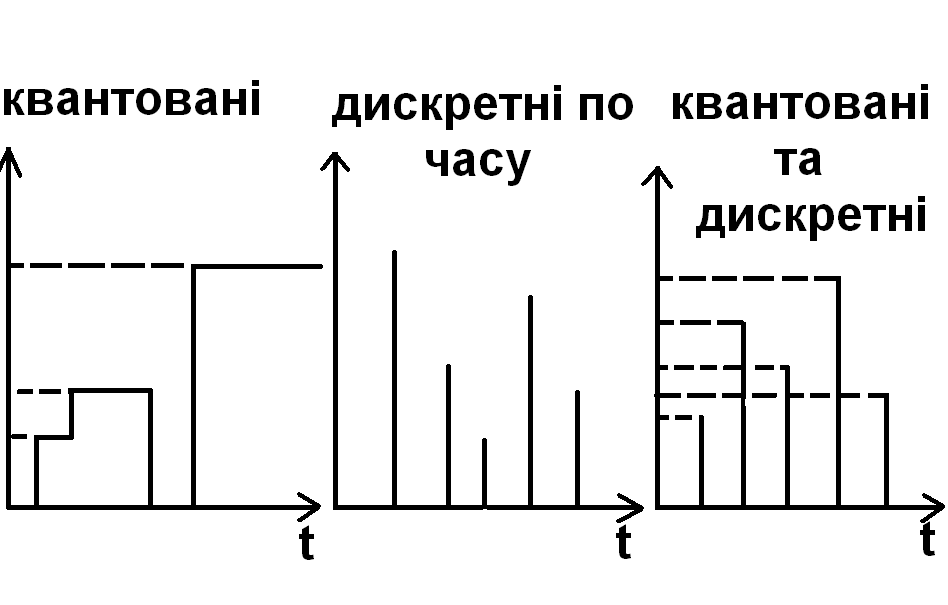

Цифрові сигнали – це дискретні сигнали, в яких квантується рівень, як правило, рівномірно і дискретизується час – рівномірно. Вони найбільш завадостійкі (існує добра система корекції – відновлення).

3. Спектральна діаграма і спектр періодичного сигналу.

Спектром сигналу називають сукупність гармонічних складових кратних частот, які характеризуються своїми амплітудами і початковими фазами, що при додаванні дають сигнал в довільний момент часу .Спектральна діаграма сигналу представляється графічним зображенням амплітуд кожної гармоніки ряду Фур'є і відповідними початковими фазами.

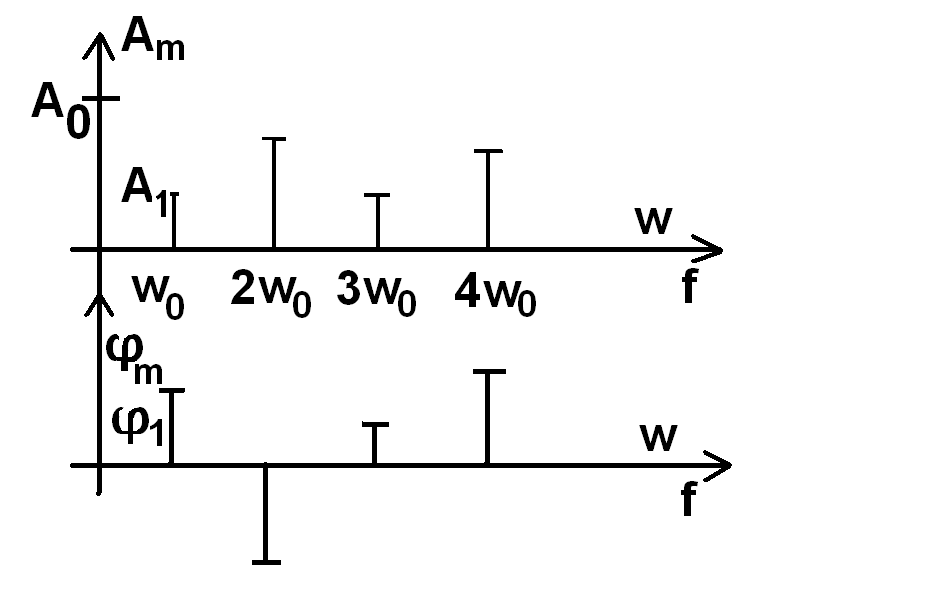
Часто в літературі називають амплітудний спектр, а називають фазовим спектром. Спектр періодичного сигналу дискретний.

Збільшення шпаруватості сигналу приводить до розширення його спектру і, відповідно, зменшенню амплітуди складових.

В залежності від форми сигналу, необхідно представляти їх різним чином членів ряду Фур'є. В залежності від можливості пристроїв прийому та декодіровки кількість членів розкладу в ряд Фур'є може бути значно зменшено.

Так в телеграфії, яка користується прямокутними імпульсами із крутими фронтами виявляється достатнім (з умовами роботи пристроїв!) трьох гармонік.

Для сигналів вводять також поняття коефіцієнта амплітуди та коефіцієнта форми.

—коеф. амплітуди

- коеф. форми

Де

Для гармонічного коливання розраховуються на портативному

F=1,11

для прямокутного

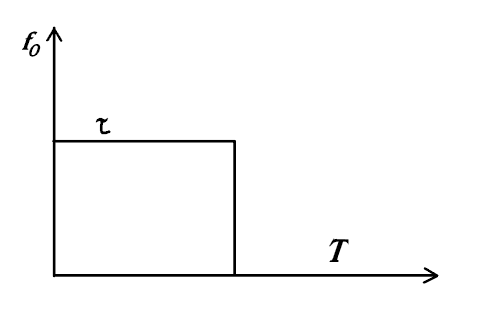
Тому

; Якщо ввести поняття шпаруватості

То С=

Ще раз відмітимо: Взагалі кажучи довільний сигнал (окрім штучно утворених набором певних гармонік) має необмежений спектр. Однак завжди можна вказати спектральну полосу F (спектр знаходиться в інтервалі (0,F )), що 95% всієї енергії знаходиться всередині даної полоси.

4. Інтегральні перетворення Фур'є. Властивості комплексної спектральної густини. Фізична суть спектральної густини амплітуд.

Неперіодичними сигналами є сигнали значення періоду яких може бутиТ . Тоді дискретне представлення рядів Фур’є неперіодичної функції

неможливе.

Розглянемо неперіодичний (імпульсний) сигнал, часова залежність якого

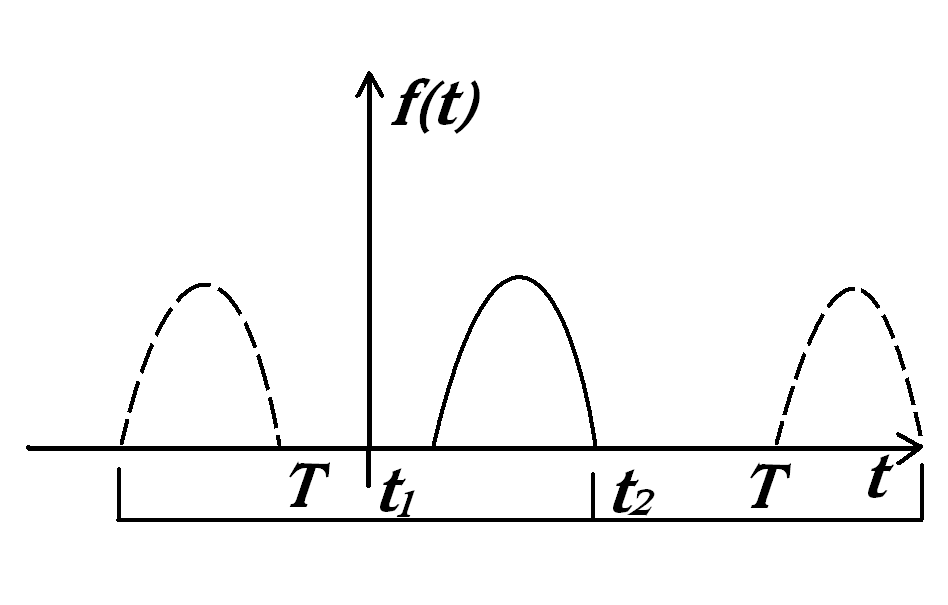
і періодично його продовжимо з будь-яким періодом Т, ясно що .Тоді такий періодичний сигнал можна представити рядом Фур’є. Оскільки

— то базова частота при і переходить в відповідний інтервал.

Для спектрального аналізу даної функції використовується інтегральне представлення Фур'є (інтеграл Фур'є)

U(t) – сигнал

де - називається комплексною спектральною густиною U(t).

Аналогічно комплексним коефіцієнтом ряду Фур'є

- дійсна частина, модуль комплексної спектральної густини.

Модуль, або спектральна густина амплітуд а функціональна залежність амплітудним спектром.

- аргумент , а його залежність від ( ) називають фазовим спектром.

За визначенням - парна функція частоти. - непарна!!! - дійсна функція.

Рівність нулю забезпечується відсутністю комплексної частини це реалізується у випадку:

та з очевидністю.

Для прикладу розглянемо амплітудний спектр дзвінко подібного сигналу

тоді

Де інтеграл Пуассона.

Зауважимо, що протяжний, довгий імпульс має значно вужчий спектр аніж вузький. І вузькому спектру завжди відповідає широкий імпульс сигналу.