2. Сигнали електрозв’язку. Класи сигналів і їх математичний опис. Неперервні, дискретні і цифрові сигнали.

2. 1. Сигнал зв’язку і його математична модель.

В канальних умовах зв’язку сигнал на приймачі не може бути описаний завідомо деякою функцією, бо тоді б не передавалась інформація. Завада створює частину даного сигналу, тому відділити її від корисного сигналу неможливо. Тому і сигнал, і завада, взагалі кажучи, – випадкові величини.

Сигнал в електрозв’язку можна розглядати як часову залежність електричних величин I, U, електромагнітні коливання, потік енергії і т. д. Детермінованими називають сигнали, які можуть бути описані функцією. Детермінованими є відомі сигнали, тобто сигнали, що створені перед лінією зв’язку. (Якщо знехтувати завадами, що виникають в пристроях при кодуванні та модуляції.) Часова залежність сигналу називається осцилограма. Математична модель сигналу містить істотні його характеристики, тобто являється спрощеною. Один і той же сигнал можна отримати за допомогою різних моделей, де виділяють ті чи інші основні властивості.

2.1.1.Класи сигналів.

Класифікують сигнали по різним ознакам :

1. За формою : прості і складні.

2. За інформативністю : детерміновані та випадкові.

3. За характером часової залежності : неперервні, дискретні.

Прості сигнали – детерміновані і можуть бути отримані за допомогою функції. Складні – суперпозиція простих.

Гармонічний сигнал отримується виразом :

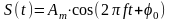
де 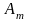– амплітуда, f – частота, t – час, φ₀ – фаза, – кругова частота.

Імпульсними є сигнали обмежені в чомусь. Поділяють на

Відеосигнал: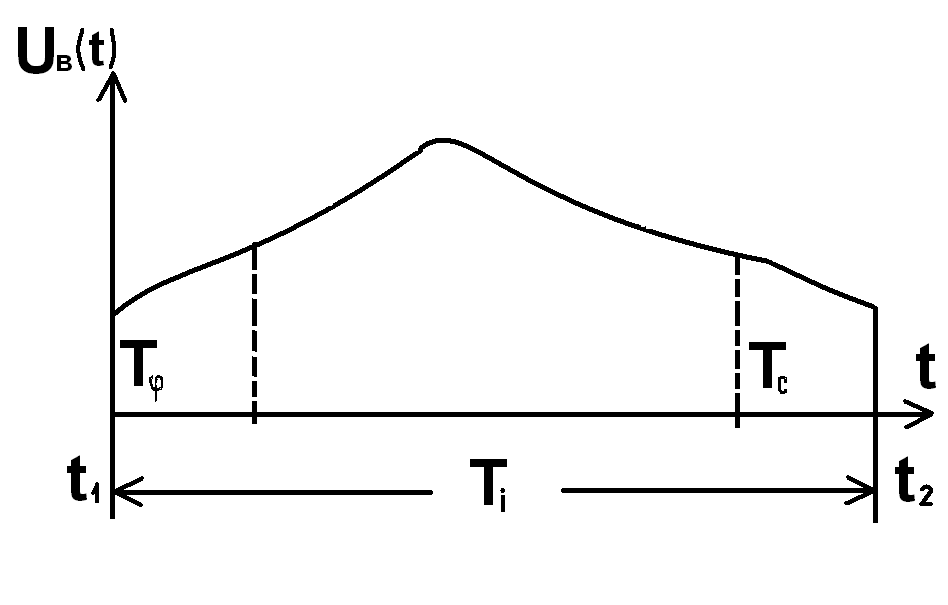

Радіосигнал:

U_p(t) = U_В(t)·cos(ωt + φ₀),

де T_i – тривалість,

– тривалість тракту (росту відеосигналу),

T_c –тривалість спаду.

В ТЕЗ найбільш поширеними є прямокутні імпульси, періодичні та не періодичні. Періодичні імпульси характеризують щільністю :

S = T_i/T; S = T_i/(T-T_i)

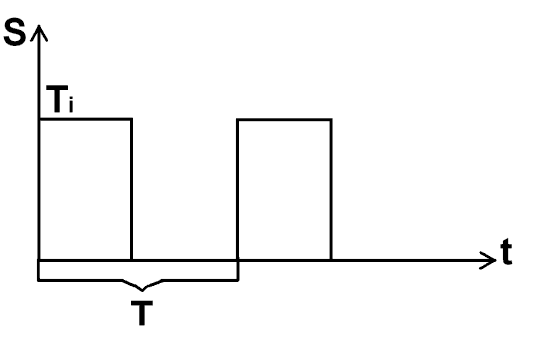
Для вивчення перехідних процесів в системі використовуються надзвичайно короткі великої амплітуди сигнали. Їх математичний опис – введення δ-функції: при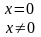

2.1.2.Складні сигнали.

Введемо спочатку поняття системи базисних функцій.

Система базисних функцій володіє повнотою тоді, коли довільну функцію можна представити у вигляді суми базисних функцій з деякими числовими коефіцієнтами.

{ψ_k(t)} – базисна система k ÷ 0,….∞,

f(t) – довільна функція.

Являється ортонормованою тоді, коли

А, -А – границі інтегрування, визначаються додатково.

Систем базових функцій є безконечна множина. Вибір базових функцій проводиться у відповідності до тих задач, які ставляться. У багатьох випадках вибір диктується швидкому збігу ряду, тобто

n – якомога мале число.

Довільний складний сигнал може бути представлений як сукупність простих, що описуються однією з системи базисних функцій (наприклад гармонік).

2.1.3.Неперервні, дискретні та цифрові сигнали.

Неперервні сигнали – це сигнали, які описуються неперервною функцією f(t), яка приймає «0» значення в скінченій кількості точок за довільний проміжок часу.