1 Ж

. Теорія електрозв`язку

1. Кодування. Декодування. Класифікація кодів.

Кодування – використовується при перетворені дискретних повідомлень у первинний сигнал.

Декодування – операція зворотня кодуванню.

Набір знаків, з допомогою якиго формується первинне повідомлення, називають первинним алфавітом або алфавітом повідомлення. Оскільки довільний текст представляється скінченним числом елементів, то число елементів, число кодів в алфавіті скінчене, хоча для європейських мов число елементів коливається в межах 52-55, а для східних – налічує кілька тисяч. Усі ці букви – ієрогліфи – можна перенумерувати системою буква-число. (В Китаї існує старовинна заборона створювати додаткові нові ієрогліфи.)

1.2.1Двійкова система кодування

Для десяткової системи числення довільне число 1234 = 1·10³ + 2·10² + 3·10¹ + 4·10°, коефіцієнти не можуть бути більшими за 9. Тобто довільне число N можно представити

N = ....

причому ≤ 9.

Розрізняють ефективне (статистичне) та коректуюче кодування. З ціллю ефективного кодування передачі інформації і наближення її до пропускної здатності канала застосовують теорему Шенона :

для канала без завад завжди можна створити ефективну систему кодування дискретних повідомлень, у якої середнє число двійкових кодових сигналів як завгодно близько буде наближатись до ентропії джерела повідомлень.

Для створення кодування завадостійкої системи, підвищення надійності передачі інформації шляхом корекції помилок користуються наступною теоремою Шенона :

для канала з завадами завжди можна знайти таку систему кодування, при якій повідомлення будуть передаватись з скільки завгодною точністю, лише коли інформаційна потужність джерела менша за пропускну здатність системи (каналу).

Для системи з основою числення m (m – ціле число ) довільне число представляється як:

Причому

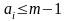
Для систем електрозв’язку доцільно використовувати двійкову систему числення m=2, бо її легко ідеалізувати. Довільне число представляється з допомогою набору 0 та 1. Наприклад

Отже, число

При кодуванні проходить процес перетворення елементів повідомлення за допомогою кодових символів в кодові комбінації → 10100 (кодові слова). Наприклад, для української мови повідомлення можна сформувати з допомогою кодових символів 0 та 1 за допомогою кодових комбінацій, що містять 5 кодових символів :

П’ятизначний код Бодо :

А → 10000

Б → 00110

В → 01101

Г → 01010

Для азбуки Морзе :

t

Коди можуть бути равномірними і нерівномірними.

Рівномірні коди – це коди, в яких кодова комбінація містить однакову кількість кодових символів. Для рівномірних кодів кількість комбінацій буде mⁿ, де m – основа числення, n – довжина кодової комбінації. Для кода Бодо 2⁵ = 32, що достатньо для передачі усіх букв. Причому 1 передається однією полярністю (↑), 0 – іншою (↓). Час передачі слова (кодової комбінації) 5τ₀ (τ₀ – один кодовий символ). Немає необхідності в розділенні слів.

Прикладом нерівномірного коду є код Морзе. В ньому кодові символи містять всього 2 комбінації (1; 0) або ж (111 та 000). Окремий кодовий символ 0 служить розділенням кодових комбінацій.

Б → ···

τ₀

9τ₀ 3τ₀

3τ₀ – це область розділення однієї кодової комбінації від іншої.

1 –відповідає крапка, 111 – тире.

При передачі кодом Морзе час передачі мінімальної комбінації Е (·) – 4τ₀; а самої довгої цифри 0 – 22τ₀; середній час – 9,5τ₀, що приблизно в "2" рази довше кода Бодо.

По завадозахищенності коди є звичайними і коди з корекцією. Звичайні використовують всю сукупність кодових комбінацій, тому заміна 0 → 1 або 1→ 0 приводить до передачі неправильної інформації. Якщо ж не всі кодові комбінації використовуються, то поява помилки може бути визначена і помилка в ряді випадків може бути скоректована. Для створення коректуючих кодів необхідно мати надлишкову кількість кодових комбінації.

Отже, дискретне повідомлення може передаватися з допомогою пристрою з слідуючою функціональною схемою :

кодер

модулятор

канал

демодулятор

Повідомлення Код Відеосигнал ВЧ сигнал Прийнятий сигнал

01011

А

01011

Відеосигнал код

Довільний сигнал отримується модуляцією, тобто характеризується часовою зміною одного або кількох параметрів одночасно. Немодульований сигнал не несе інформацію!!!

Якщо функція f (a, b, c, d) – характеризує перепищик інформації, то модуляція полягає в встановленні певної, у відповідності з повідомленням часової належності одного з параметрів.

Наприклад :

C = C₀ + ∆C·U(t) = C₀[1 + (U/C₀)·U(t)], m – коефіцієнт модуляції.

Якщо модулюється параметр c → с-модуляція, якщо b → b-модуляція.

Для гармонічного перепищика, тобто такого, що описується залежністю

f(t) = A·h̉_n·(ωt + φ)

маємо три параметри, що можна модулювати :

АМ → A = A₀ + A·U(t)

ФМ → φ = φ₀ + ∆φ·U(t)

ЧМ → ω = ω₀ + ∆ω·U(t)

Якщо повідомлення передається кодовими символами 0 та 1, говорять що проводиться не модуляція, а маніпуляція. В сучасних системах зв’язку, особливо багатоканальних, в якості перепищика використовуються періодичні послідовності імпульсів певної форми. Параметри такої системи : A – амплітуда, T – довжина (ширина) імпульсів, φ – фаза, частота слідування. Тому існують 4 типи модуляції :

АІМ – амплітудно-імпульсна модуляція;

ШІМ – широтно-імпульсна модуляція;

ФІМ – фазово-імпульсна модуляція;

ЧІМ – частотно-імпульсна модуляція.

В системах радіозв’язку, електрозв’язку модуляція проходить в 2 етапи. Спочатку повідомлення кодується, модулюється з допомогою сукупності імпульсів, а потім проходить модуляція високочастотного коливання гармонічного типу. Тому повна модуляція сигналу проходить по типу : АІМ→АМ, ФІМ→АМ, ШІМ→ЧМ і т. д.