11) Роздільна здатність об*єктива. Критерій Релея

Усі зображаючі пристрої мають апертурну діафрагму та зіницю входу скінчених розмірів. На краях апертурної діафрагми відбувається дифракція, що принципово обмежує роздільну здатність, тобто лінійні розміри деталей об’єкта, який зображено, можна спостерігати окремо.

Переважна більшість діафрагм мають круглу форму, тому в основі теорії роздільної здатності лежить формула дифракції Фраунгофера на круглому отворі. Якщо спостерігається просто дифракція на круглому отворі, на який падає пучок світла, то умови Фраунгоферової дифракції реалізуються лише на дуже великих відстанях там, де хвильовий параметр перевищує одиницю.

Якщо в отворі розташована збиральна лінза, то вона переносить безмежність у свою задню фокальну площину.

У задній фокальній площині хвильовий фронт плоский, оскільки його кривизна змінює свій знак. У геометрооптичному наближенні зображенням нескінченно віддаленого джерела є точка. Насправді дифракція світла на апертурній діафрагмі призводить до формування в фокальній площині дифракційної картини.

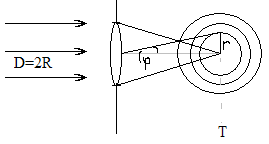
Така дифракційна картина носить назву картина Ері, а центральна пляма – пляма Ері. У центральній плямі зосереджено приблизно 90% енергії випромінювання.

Розподіл амплітуди описується за допомогою функцій Бесселя

де х – це комбінація довжини хвилі, діаметра апертурної діафрагми та геометричних умов (зокрема, фокусної відстані).

– інтенсивність (графік близький до графіка функції sinc(x)).

Якщо випромінювання поширюється від двох джерел у дуже вузьких напрямках, то такі дифракційні картини будуть накладатись і зображення не будуть розділятися.

Визначимо кутову ширину центрального кільця (максимуму) . З теорії функцій Бесселя можна визначати значення нулів, розподіл амплітуди та інтенсивності. Для дифракції на щілині шириною b раніше було отримано: .

Відповідно для центральної пелюстки: .

Аналогічно лише аналізуючи більш складні функції Бесселя для першого нуля картини Ейрі, отримаємо: .

Як і при дифракції на щілині коефіцієнт при λ близький до одиниці. З рисунка видно , отже .

Телескопи завжди працюють у параксіальному наближенні , тоді . Таким чином ми визначили як кутову ширину плями Ейрі, так і її лінійні розміри. З останньої формули видно, що розміри плями Ейрі та роздільна здатність залежать від довжини хвилі опромінення: роздільна здатність зменшується, а розміри плями Ейрі збільшуються зі збільшенням λ; з іншого боку роздільна здатність зростає, а розміри плями Ейрі зменшуються по мірі збільшення розмірів об’єктива.

Для того, щоб визначити роздільну здатність телескопа використовують різні критерії. Критерій Релея визначає граничну роздільну здатність.

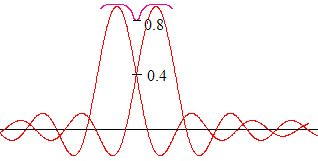
Нехай максимум від однієї дифракційної картини співпадає з першим нулем дифракційної картини другого джерела, джерела взаємно некогерентні. При такій умові інтенсивність в точці перетину графіків складає 0,4 від max, а їх сума рівна 0,8 від max. Такий перепад інтенсивності реєструється візуально, такі джерела є розділеними.

Якщо кутова відстань між джерелами зменшується, то центральний провал зникає і розділення не спостерігається.

Отже, можна вважати, що джерела розділяються, якщо кутова відстань між ними .

Величина, обернена до останньої, тобто називається роздільною здатністю.

Висновки, отримані для роздільної здатності телескопа повністю узгоджуються з якісним розглядом, який було проведено для мікроскопічного об’єктива із залученням теорії Аббе, але на відміну від оптичної телескопії в мікроскопії виникає ще одна можливість підвищення роздільної здатності. Виявляється можна підвищити роздільну здатність, використовуючи імерсію зі спеціально підібраним показником заломлення. Повне внутрішнє відбивання порушене.