5) Дифракція на гармонійній амплітудній ґратці

Дифракційною ґраткою називається довільна структура, яка періодично у просторі модулює амплітуду або фазу, або і амплітуду, і фазу падаючого пучка. Перші діючі дифракційні ґратки були виготовлені Фраунгофером на поч. XX ст. (були дуже грубими). Незважаючи на недосконалість Фраунгоферових ґраток за їх допомогою було зроблено відкриття, яке виходить за рамки оптики: виявлено темні Фраунгоферові лінії у спектрі Сонця. Це призвело до створення астрофізики.

Спостереження:

1. при падінні на дифракційну ґратку плоский пучок розкладається в набір або спектр плоских хвиль;

2. при нахиленому падінні пучка зменшується видимий період ґратки, відповідно збільшується кут дифракції;

3. в залежності від кута падіння пучка на ґратку можуть змінюватися інтенсивності дифракційних порядків.

Дифракція на гармонійних амплітудних ґратках

Така ґратка називається ґраткою Релея.

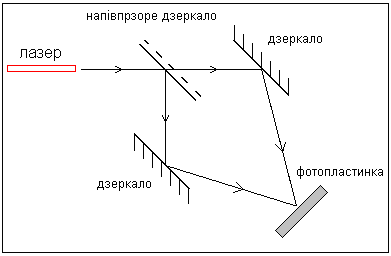
У даному випадку дифракційна ґратка – це фотографічний запис інтерференційної картини; у відповідності з періодичним розподілом інтенсивнисті записується ґратка з періодичним пропусканням. Визначимо амплітуду пропускання в залежності від координати х:

– амплітудне пропускання,

де d – постійна ґратки (просторовий період), – просторова частота.

На ґратку падає по нормалі плоска хвиля, яка поширюється в напрямку z. Результат дифракції знаходиться як добуток амплітудного пропускання ґратки та падаючої хвилі.

При дифракції на амплітудній косинусоїдальній ґратці виникають три і лише три дифракційні спектри або порядки: 0-й та ±1-й. З показників експоненти можна знайти напрямки дифракції на відповідні порядки.

Структура показників експоненти не що інше, як представлення прямих у відрізках.

0-й порядок дифракції поширюється у напрямку падаючого пучка, хвилі ±1-го порядків поширюються симетрично в напрямках, які визначаються співвідношенням довжини хвилі і постійної ґратки. З рисунка видно, що при збільшенні довжини хвилі кут дифракції буде збільшуватись. При зменшені періоду ґратки кут дифракції також буде збільшуватись.

Увесь проведений розгляд буде справедливим у випадку, коли період гармонійної ґратки порівняно з довжиною хвилі дуже великий. З кінцевого результату видно, що ані інтенсивності, ані амплітуди дифрагованих пучків не залежать від λ, так буде не завжди. Для гармонійної ґратки можна визначити максимальну амплітуду, відповідно максимальну відносну інтенсивність випромінювання, яка може фігурувати в кожному з порядків. Для цього слід задати наступну структуру амплітудного пропускання: максимальне пропускання нехай буде одиниця.

(рис)

– відносна амплітуда дифраговоного пучка першого порядку.

6. Дифракція на бінарній ґратці

Бінарними називаються ґратки, які складаються з абсолютно прозорих і непрозорих елементів. Це Фраунгоферові ґратки. (Прозорі ділянки позначаються як і щілини.)

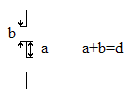
Знайдемо формулу ґратки, а саме умову дифракційного максимуму.

З практики відомо, що пучок, який продифрагував на ґратці, розщеплюється в набір пучків, що поширюються в різних напрямках. Розглянемо умову інтерференційного підсилення. До ґратки хвильовий фронт – плоский: між парціальними пучками, на який можна розбити хвильовий фронт, різниці фаз не існує. З певного положення парціальні пучки також не набувають різниці фаз. Визначимо період як відстань між відповідними точками сусідніх штрихів. Умова інтерференційного підсилення випромінювання, що виходить з цих точок, полягає у тому, що протилежний катет буде дорівнювати довжині хвилі опромінення λ: , де φ – кут дифракції. Якщо використати таку умову, то різниця ходу між відповідними точками через період дорівнює 2λ. Таким чином має місце багатопроменева інтерференція випромінювання і при визначальній умові виникає відповідний дифракційний порядок. У більш загальному випадку для m-го порядку дифракції вимагається, щоб . – умова інтерференційного підсилення (пучки – синфазні). Фізичний механізм дифракції на бінарній ґратці полягає в наступному: безпосередньо за ґраткою дифракційні порядки ще не формуються, з кожної прозорої ділянки випромінюється ненапрямлена циліндрична хвиля приблизно так, як і при дифракції на щілині. Лише у процесі поширення таких парціальних хвиль і реалізації умов інтерференційного підсилення формуються напрямлені плоскі хвилі, а саме дифракційні порядки. Таким чином дифракцію на ґратці слід розуміти як двоетапний процес:

• І етап – дифракція на ґратці як на сукупності щілин;

• ІІ етап – інтерференція парціальних дифрагованих пучків.

Тому картина, яка спостерігається за ґрат кою, часто називається дифракційно-інтерференційною. Як і при використанні еталона Фабрі-Перо, де реалізується багатопроменева інтерференція, такий самий випадок має місце і при дифракції на ґратці. Як завжди багатопроменева інтерференція забезпечує високу роздільну здатність при її використанні у спектральних приладах. Для великих ґраток з малим періодом максимальний порядок інтерференції k може складати . У даному випадку максимальний порядок інтерференції визначається для крайніх точок ґратки – це різниця ходу між крайніми хвилями, виражена в одиницях довжин хвиль. Вищою роздільною здатністю, ніж дифракційні ґратки, володіє лише еталон Фабрі-Перо.

Формули ґратки визначають напрямки , в яких можуть виникнути дифракційні порядки при заданих d і λ, але деякі з цих порядків, які передбачаються формулою ґратки, можуть і не виникати.

Розглянемо випадок коли , тобто в даному випадку прозорі і непрозорі ділянки по можливості однакові. Визначимо умову ІІ-го дифракційного максимуму:

Якщо розглядата дифракцію на окремій прозорій ділянці штриха, буде виконуватися умова: . Це означає, що в одному і тому напрямку реалізуються умови ІІ-го дифракційного максимума як на ґратці в цілому та І-го нуля функції sinc при дифракції на щілині. Отже, жодна щілина з такою шириною не випромінюватиме у цьому напрямі. При цьому 2-гі, 4-ті, 6-ті та всі парні порядки випадають. Аналогічно можна знайти умову, коли будуть зникати кожний третій і т.д.