4) Дифракція на круглому отворі і непрозорому диску

Як би не обирали пробну точку Р, інтенсивність світла буде відмінною від нуля. В основі теорії дифракції лежить принцип Гюйгенса–Френеля. Вперше він був сформульований наприкінці XVII ст. і в першому формулюванні цей принцип носив не фізичний, а суто геометричний характер, зокрема Гюйгенс навіть не використовував основний параметр хвильової оптики такий, як довжина хвилі, тобто поширення світла не пов’язувалось з просторовим періодом λ.

На початку XIX ст. незалежно Юнг і Френель ввели хвильові уявлення щодо природи світла і Френель поєднав принцип інтерференції з принципом Гюйгенса, оскільки тепер поширення розглядалося як хвильовий рух і враховував фазові співвідношення між випромінювачами, то в такій постановці цей принцип є фізичним. Первинне джерело оточується довільною замкнутою поверхнею S, точки цієї поверхні розглядаються як вторинні випромінювачі з такими амплітудами і фазами, з якими до даної точки поверхні дійшло випромінювання від первинного джерела.

Якщо задати такі амплітуди і фази вторинних випромінювачів, то наступне положення хвильового фронту можна знайти як результат інтерференції хвиль від таких вторинних випромінювачів. В часи Френеля панувала теорія пружного ефіру і такі вторинні випромінювачі вважалися реальними, тобто це частинки ефіру, які поглинають світло, а потім випромінюють. Згідно електромагнітної теорії світла, ефір відсутній і світло може поширюватись в абсолютному вакуумі. Таким чином вторинні джерела є віртуальними. Тим не менше принцип Гюйгенса–Френеля повністю зберігає своє значення як рецепт для обчислення поля, яке виникає при дифракції світла. Оскільки замкнену поверхню навколо реального первинного джерела можна обрати довільним чином, то її, як правило, обирають з міркувань зручності: якщо первинне джерело точкове, то обирають сферичну поверхню. Принцип Гюйгенса–Френеля дозволяє пояснити з фізичної хвильової точки зору прямолінійне поширення світла.

Закон прямолінійного поширення постулюється в геометричній оптиці, але не доводиться. Для пояснення прямолінійного поширення світла використовують метод зон Френеля: розглядається точкове джерело, від якого поширюється сферична хвиля; визначається радіус хвильового фронту і відстань від хвильового фронту до точки спостереження b; з точки спостереження виконують наступну побудову: сферичний хвильовий фронт розбивається на кільцеві зони за певним правилом (λ/2).

Кожна наступна зона віддалена від попередньої на λ/2. Виявляється, що зони Френзеля мають однакові площі, а отже, амплітуди випромінювання з сусідніх зон, що потрапили у точку B практично однакові. При цьому за побудовою внески від сусідніх зон є протифазними, це означає, що випромінення з сусідніх зон Френеля практично повністю інтерференційно компенсують одне одного у точці B. Розташуймо при заданому положенні хвильового фронту непрозорий екран з круглим отвором, який виділяє з хвильового фронту лише першу центральну зону Френеля. Внесок першої зони Френеля не скомпенсований інтерференційно дією інших зон, тому інтенсивність в точці b буде високою. Зі збільшенням розмірів отвору так, щоб він охоплював вже перші дві зони Френеля, їх внески компенсуються і в точці B інтенсивність практично падає до 0. Відкривши третю зону Френеля, отримаємо max інтенсивності. Загальне правило полягає у тому, що коли відкрита непарна кількість зон, то спостерігається max, а коли парна – min.

Збільшуючи і далі розміри отвору і відкриваючи весь хвильовий фронт, можна вважати, що дія ІІ-ї зони компенсується ІІІ-ою, дія ІV-ої – V-ою і т.д., отже залишається внесок лише від центральної зони Френеля. Це означає, що світло з т.А поширюється в т.B вздовж вузького каналу, співрозмірного з центральною зоною Френеля. Він і є фізичним образом променя, який фігурує в геометричній оптиці.

Розглянемо послідовно внески від різних зон Френеля; це дасть можливість обґрунтувати наступне твердження: дія всього хвильового фронту еквівалентна половині дії центральної зони Френеля, але не дії половини зони Френеля.

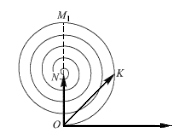
Центральна зона Френеля розбивається на елементарні комірки і в т.B сумуютьсяїх внески. Зрозуміло, що оскільки хвильовий фронт сферичний, то у площині фази електромагнітних хвиль будуть плавно змінюватись по мірі віддалення від центраСпіраль майже замкнеться. Френель постулював коефіцієнт нахилу – залежність амплітуди вторинного випромінювача від кута: амплвтуда вторинного випромінювача пропорційна косинусу кута дифракції; вторинний випромінювач не випромінює вздовж хвильового фронту, оскільки . Френель побудував теорію дифракції, не виходячи з хвильового рівняння, тому постулювання коефіцієнту нахилу є помилковим. Хоча у параксіальному наближенні теорія Кірхгофа та експеримент дозволяють користуватися твердженням Френеля.

Дифракція на доповнювальному екрані

Доповнювальним до даного називається такий дифракційний пристрій, в якому світлі ділянки замінені на непрозорі ділянки, але зберігається геометрія досліду, тобто відстань від первинного джерела С до екрану та від екрану до точки спостереження Р, а також довжина хвилі.

Доповнювальним пристроєм до непрозорого екрану зі щілиною буде непрозорий диск таких же розмірів, що і щілина.

Пуассон стверджував, у разі правильності розгляду Френеля в точці спостереження,а саме в області геометричної тіні за непрозорим диском повинен спостерігатись max інтенсивності.

За Пуассоном, диск вилучає певну кількість зон Френеля з низькими номерами, тому дія хвильового фронту, який залишився відкритим повинна бути такою, як дія першої зони Френеля, яка залишається відкритою.

Оскільки диск має круглу форму, то для точки спостереження на осі виконується принцип таутохронізму. Отже, усі парціальні сигнали, що проходять повз, диск виявляються в точці Р синфазними і тому інтерференційно підсилюються. Цей висновок підтверджено експериментально, така пляма отримала назву плями Пуассона або Пуассона–Араго.

Отже, якщо диск блокує n початкових зон Френеля, то світло на осі зумовлюється n+1-ою зоною Френеля, як і при розгляді дифракції на круглому отворі, внесок від n+2-ої та n+3-ої зони інтерференційно компенсується, n+4-ої та n+5-ої також і т.д. Таким чином дифракція на круглому отворі і на доповнюльному непрозорому диску має різну структуру. При дифракції на круглому отворі в залежності від відстані, на якій проводиться спостереження ,на осі знаходиться max або min. Оскільки для різних відстаней в отворі знаходиться різна кількість зон Френеля. Зі збільшенням відстані від екрану до точки спостереження кількість зон Френеля зменшується. Навпаки при дифракції на диску: незалежно від відстані до площини спостереження в центрі завжди max . Це справедливо для так званих Френелівської дифракції або дифракції ближнього поля.