3.2.2. Геодезична лінза

Г

Рис. 3.2.2

еодезична лінза (рис. 3.2.2) являє собою заглиблення сферичної або асферичної форми. Вісь симетрії заглиблення перпендикулярна до площини хвилеводу. Край заглиблення утворює круговий контур. Заглиблення робиться до нанесення хвилевідного шару. Після нанесення хвилеводу область з такою лінзою набуває фокусуючих властивостей. Довжина оптичних шляхів для променів, які проходять через різні ділянки геодезичної лінзи різні, і аналогічні затримкам звичайної лінзи.

3.2.3. Дифракційні лінзи

Р

Рис. 3.2.3

озглянемо деяку дифракційну структуру, зображену на рисунку 3.2.3. Нехай період дифракційної решітки змінюється в напрямку . Паралельний пучок опромінює цю структуру перпендикулярно до осі . Уявімо собі, що всі промені, які пройшли через структуру, зберуться в одну точку на відстані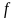 . Постає питання, яка повинна бути закономірність зміни періоду решітки?

Тангенс кута в цьому випадку дорівнює:

. (3.2.1)

За формулою решітки кут дифракції першого дифракційного порядку визначається виразом:

. (3.2.2)

З (3.2.1) і (3.2.2) маємо:

. (3.2.3)

Якщо вхідний отвір лінзи набагато менше ніж то та (3.2.3) перетворюється до вигляду:

, (3.2.4)

або, якщо виконується ще більш жорстоке наближення 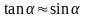, то

, (3.2.5)

О

Рис. 3.2.4

тже, якщо виготовити решітку з змінним періодом, який змінюється у відповідності до (3.2.3), то така дифракційна структура буде працювати як лінза. Як відомо, такі структури отримали назву лінза Френеля, або дифракційна лінза. В інтегральній оптиці подібні лінзи можна отримати, якщо на хвилевід нанести за закономірністю (3.2.3) додатковий шар з іншим коефіцієнтом заломлення. У цих місцях випромінювання буде виводитися з хвилеводу. Отже, те, що буде розповсюджуватися в шарі, буде відповідне дифракційне поле, яке збереться у точку на відстані . Для підвищення ефективності такої лінзи іноді форму штрихів виконують у вигляді, зображеному на рис. 3.2.4 (аналог товстої голограми). Ефективність такої лінзи може сягати 100 %.

7.Модулятори-перемикачі на основі ефекту тунельної перекачуванни світла, або модулятори-перемикачі на зв’язаних хвилеводах

О

Рис. 4.1.2

снову електрооптичних модуляторів-перемикачів на базі зв’язаних хвилеводів складають два (або більше) близько розташованих паралельних керованих хвилеводи. На рисунку 4.1.2, представлений модулятор-перемикач X-типу. При збудженні одного з них у процесі розповсюдження випромінювання відбувається перерозподіл енергії між хвилеводами, який залежить від прикладеної до керуючих електродів напруги. Суть явища перерозподілу енергії полягає в наступному. Якщо хвилеводи розташовані на невеликій відстані 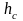, то хвости хвилевідних мод, які виходять за межі хвилеводів, перекриваються. Отже, виникає розподілений зв’язок між полями хвилеводів. Такий розподілений зв’язок має низку унікальних властивостей. Насамперед, це те, що для його виникнення не потрібні інші конструктивні елементи. Треба тільки зсунути хвилеводи на достатньо малу відстань. Зв’язок такого типу має неперервний характер. Наприклад, якщо змінювати відстань між хвилеводами вздовж структури, отримаємо в кожному місці свій коефіцієнт зв’язку. Це дозволяє формувати складні інтегрально-оптичні пристої, наприклад, на одній хвилевідній лінії формувати модулюючі пристрої з різним функціональним призначенням.

Еомплексні амплітуди електричного поля змінюється у хвилеводах за закономірністю:

, (4.1.4)

де – коефіцієнт зв’язку. Спочатку енергія з хвилеводу 1 перекачується в хвилевід 2, а потім починається обернений процес.

Отже, у системі з двох хвилеводів виникає щось подібне до коливного процесу.

Повна перекачування енергії між хвилеводами відбувається на так званій довжині зв’язку . Якщо на довжині відбувається повна перекачування енергії, то такий стан системи називається схрещеним. Якщо, перекачування енергії не відбувається і світло виходить з того ж самого хвилеводу, в який поступало, то такий стан системи називають паралельним.

Відзначимо, що як випливає з (4.1.4) фази випромінювання в хвилеводах зсунуті на .

Д одамо, що 100-відсоткова ефективність перекачування відбувається лише у випадку, коли константи розповсюдження мод в обох хвилеводах абсолютно узгоджені. Відповідно товщини та коефіцієнти заломлення хвилеводів повинні ретельно контролюватися.

Г

Рис. 4.1.3

оловний недолік таких елементів – неможливість на практиці реалізації 100 % ефективності. Наприклад, неможливе виготовлення хвилеводів з довжиною, яка точно дорівнює . Проте схему можна зробити двосмуговою і одночасно змінювати асиметрично параметри у двох хвилеводах. Окрім цього, напругу можна подавати на таку схему на різні лінії з різною полярністю. Тоді в одному хвилеводі показник заломлення буде збільшуватися, а в другому – зменшуватися.

. (4.1.5)

Отже, маємо відносну зміну константи розповсюдження удвічі більшу, ніж у системі з одним електродом.

На рисунку 4.1.3 представлений Y-розголужувач, якій працює за аналогічним принципом, але перекачування енергії хвилі відбувається одночасно у два канали.