28 И

1. Дисперсійне рівняння хвилеводу

Знову розглянемо тришарову структуру (рис. 2.2.1), для якої знову виконується умова .

У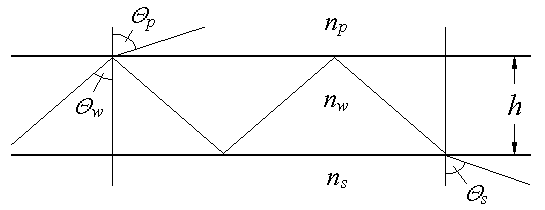 явімо, що у хвилеводі розповсюджується деяка плоска хвиля під кутом 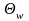до нормалі до поверхні хвилеводу. Природно, що виконується інваріант Снелліуса:

Рис. 2.2.1

, (2.2.1)

звідки для кута маємо:

. (2.2.2)

Швидкість розповсюдження будь-якої хвилі в середовищі хвилеводу однакова для будь-якого . Але, якщо розглядати розповсюдження хвилі вздовж осі , то її швидкість (константа розповсюдження) залежить від цього кута (для різних маємо різні оптичні шляхи). Константа розповсюдження хвилі може бути описана співвідношенням:

. (2.2.3)

Величина

(2.2.4)

має назву ефективного показника заломлення.

Для кутів і , як відомо, спостерігається повне внутрішнє відбивання. Отже, світлова хвиля, яка розповсюджується під кутом (оскільки ) не залишає середовища хвилеводу. Зауважимо, що при відбиванні хвилі від границі розділу, хвиля набуває додаткового зсуву по фазі (так звана поправка Гауса-Хенхена):

Для ТЕ-моди:

. (2.2.5)

Для ТМ-моди:

. (2.2.6)

де .

Наявність таких фазових зсувів з точки зору геометричної оптики можна пояснити лише в один спосіб. Хвиля на границі розділу відбивається не зразу, а занурюється на певну відстань у середовище, яке межує з хвилеводом (див. рис. 2.2.2).

Ф азові зсуви в цьому випадку визначається подвійним оптичним шляхом .

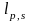З

Рис. 2.2.2

умов повного внутрішнього відбивання не випливає ніяких фізичних обмежень на кути, під якими розповсюджується хвиля у хвилеводі. Але:

1. Хвиля, яка розповсюджується в хвилеводі, абсолютно когерентна, тобто довжина та час когерентності необмежені.

2. Фронт хвилі також необмежений у просторі.

У

Рис. 2.2.3

такому випадку коливання в будь-якій точці хвилеводу є суперпозицією необмеженої кількості багатократно відбитих від границь хвилеводу хвиль, які взаємодіють між собою. Ці хвилі можуть підсилювати одна одну або гасити, якщо розповсюджуються у фазі або в протифазі. Коли кути такі, що коливання підсилюються, то кажуть, що виконується умова самоузгодження.

Умова самоузгодження виконується, якщо виконується співвідношення (див. рис. 2.2.4):

або . (2.2.6)

З рисунка випливає, що:

та (2.2.7)

Якщо врахувати фазові зсуви, які виникають при повному внутрішньому відбиванні, то в кінцевому вигляді умова самоузгодження має таку форму:

. (2.2.8)

Вираз (2.2.8) називають дисперсійним рівнянням. Це трансцендентне рівняння розв’язки якого дають набір кутів 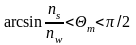. Цей набір кутів визначає кути плоских хвиль, які можуть розповсюджуватися у хвилеводі, а також відповідні їм ефективні показники заломлення та константи розповсюдження, тобто визначає характеристики хвилевідних мод.

2.2.3. Ефективна товщина хвилеводу

Як стверджувалася раніше, хвиля, яка розповсюджується у хвилеводі занурюється в середовища покривного шару та підкладенки. Отже, шар, в якому відбувається хвилевідний процес має більшу товщину ніж геометрична товщина хвилевідного шару. Будемо називати товщину хвилевідної структури , в якій передається 90 відсотків енергії хвилі (стандартний критерій), ефективною товщиною хвилеводу. Знайдемо цю величину.

Знайдемо відстані, на яких інтенсивність ТЕ-хвилі в зонах І і ІІІ зменшується в 10 разів. Для цього використаємо 1-ше та 3-тє рівняння співвідношення (2.1.6). Така умова виконується, якщо амплітуда поля в зонах І і ІІІ зменшується в разів.

Отже, відстані і можна знайти з співвідношень:

. (2.2.9)

З (2.2.9) випливає:

; (2.2.10)

. (2.2.11)

З ауважимо, що величини і та як наслідок ефективна товщина (як і відповідні модові характеристики) залежать не тільки від параметрів хвилеводу підкладенки, покривного шару, але й від довжини хвилі ( ).

Н

Рис. 2.2.4

а рисунку 2.2.4 наведено якісну структуру типів коливань, які реалізуються в хвилевідній структурі для різних констант розповсюдження. У відповідності до величини цієї константи умовно розрізняють моди покривного шару, підкладенки та хвилевідні моди. Ілюстрація наведена для випадку коли показник заломлення підкладенки більше, ніж показник заломлення покривного шару ( ).

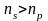Отже, безпосередньо у хвилеводі можуть існувати лише окремі типи коливань – хвилевідні моди. Кути, під якими вони розповсюджуються, визначаються з дисперсійного рівняння. В деякому сенсі можна стверджувати, що процес розповсюдження хвилі має зигзагоподібний характер.

При цьому:

1. Чим менше номер моди, тим більший кут їй відповідає.

2. Чим менше номер моди, тим менше вона занурюється в навколишнє середовище.

3. Чим більше номер моди, тим вона менш потужна (якщо коефіцієнт поглинання хвилеводу невеликий). Мода з номером 0 є головною модою і вона найбільш потужна.