1.1.Механическое дв-ние

Механика состоит из трёх разделов: 1)Кинематика (исследует пространственно-временное перемещение тел и оперирует такими понятиями как время t, путь S, скорость v и ускорение a. Механич.дв-ние изучается без учёта св-в самого тела и причин, вызвавших дв-е) 2)Динамика (изучает дв-ние материальных тел и оперирует понятиями силы и массы) 3)Статика (изучает условие равновесия сис-мы тел, на кот. действуют внешние силы. Объектам присуща пространственная протяженность, а время в механике характеризует последовательность череды меняющихся событий. Сис-ма отсчета – совокупность системы координат и тело или группу тел, относительно кот. рассматривают дв-ние. Простейшая сис-ма отсчёта – декартная сист.координат. Механ.дв-ние – взаимное изменение расположения тел в пространстве и времени, является относительным, т.к.происходит относительно чего-либо. Объект представляют материальной точкой, т.е.телом, размерами и формами кот. пренебрегают. При дв-нии точка описывает кривую, называемую траекторией. Траектория бывает прямая и криволинейная. Участок, пройденный за некоторое время – длина пути. Закон дв-ния – формула, позволяющая в любой момент времени определить положение точки, её v, a, S. S=f(t) –зависимость пути от времени. В случае трёхкоординатной системы используют три уравнения по каждой из координат. Определяя соответствующие координаты, можно построить полную траекторию тела.

1.2. Зависимость проводимости полупроводников от температуры

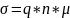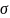Завис-ть проводимости от t любого мат-ла опред-ся температурными завис-ми, концентрацией и подвижностью носителей заряда. , где - проводимость.

В метал. и многих полупроводниках подвижность почти не зависит от t. Завис-ть проводимости определ-ся температурной завис-тью концентрацией носителей заряда. В полупроводниках эта завис-ть очень сильная. В полупроводниках атомы при тепловых колебаниях взаим-ют не только др. с др., но и с эл-нами, кот.они могут передавать часть энергии. Приобретая энергию, эл-ны могут преодолевать запрещенные пространства. Вероятность того, что эл-н преодолеет запрещенную зону пропорциональна 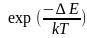. В полупроводниках число тепловых возбуждений в секунду пропорционально числу эл-нов у края заполненной зоны, числу пустых мест в зоне провод-ти, вероятности что какой-либо атом приобретёт энергию достаточную для переброса энергии через запрещенное пространство. Т.О, число тепловых возбуждений опред-ся соотношением 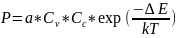, где 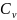- число эл-нов у края зоны, 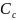- число вакансий в зоне провод-ти, a – коэф.,зависящий от чистоты столкновения.

Т.О.,концентрация носителей заряда, определ-маячислом тепловых возбуждений, экспоненциально растёт с t, =>идеальная провод-ть имеет ту же зав-ть, т.е.подчиняется ур-нию Арениуса ;

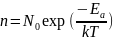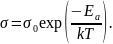
Если Ea(энергия активации), она может равняться запрещ.зоне(ширине запрещ.зоны), а также глубине залегания примесного ур-ня. Чтобы опред-ть Ea достаточно знать концентрацию или провод-ть при 2-ух t.

ln 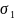=lnσ₀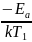

lnσ₂=lnσ₀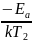

В ряде полупровод. подвижность также эксп-но растет с t. В этом случае для опр-я ширины запрещ. зоны необх-мо знать зав-ть конц-ции и подвижн-ть по отдельности.

1.3. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА. Магнитные моменты электронов и атомов

Магнитные свойства вещества объясняются согласно гипотезе Ампера циркулирующими внутри любого вещества замкнутыми токами: внутри атомов, вследствие движения электронов по орбитам, существуют элементарные электрические токи, которые создают элементарные магнитные поля.

Поэтому:

1. если вещество не обладает магнитными свойствами - элементарные магнитные поля несориентированы ( из-за теплового движения);

2. если вещество обладает магнитными свойствами - элементарные магнитные поля одинаково направлены (сориентированы) и образуется собственное внутреннее магнитное поле вещества.

Различные среды при рассмотрении их магнитных свойств называют магнетиками.

Все вещества в той или иной мере взаимодействуют с магнитным полем. Намагничивание материалов происходит за счет токов, циркулирующих внутри атомов – вращения электронов и движения их в атоме. Поэтому намагничивание вещества следует описывать при помощи реальных атомных токов, называемых амперовскими токами.

Если магнитное поле слабо усиливается в веществе, то такое вещество называется парамагнетиком: если ослабевает, то это диамагнетик: Но есть вещества, обладающие сильными магнитными свойствами. Такие вещества называются ферромагнетиками: Эти вещества способны сохранять магнитные свойства и в отсутствие внешнего магнитного поля, представляя собой постоянные магниты.

Все тела при внесении их во внешнее магнитное поле намагничиваются в той или иной степени, т.е. создают собственное магнитное поле, которое накладывается на внешнее магнитное поле.

Магнитные свойства вещества определяются магнитными свойствами электронов и атомов.

Магнетики состоят из атомов, которые, в свою очередь, состоят из положительных ядер и, условно говоря, вращающихся вокруг них электронов.

Электрон, движущийся по орбите в атоме эквивалентен замкнутому контуру с орбитальным током: I=ev. где е – заряд электрона, v– частота его вращения по орбите.

2.1.Связь между линейными и угловыми скоростями и ускорениями

Для описания движения материальной точки по окружности кроме линейной скорости введено понятие угловой скорости.

Угловой скоростью w наз-ют величину, равную отношению угла поворота Df радиуса-вектора точки, движущейся по окружности к промежутку времени Dt, в течение кот. произошел этот поворот:

w=Df/Dt. (1.27)

Для равномерно движущейся по окружности точки

w=f/t. (1.28)

Единица угловой скорости устанавливается из формулы (1.28). В СИ за единицу угловой скорости принята скорость такого равномерного движения точки по окружности, при котором радиус-вектор этой точки в течение 1 с поворачивается на угол 1 рад. Эту единицу угловой скорости обозначают 1 рад/с и называют радиан в секунду.

При равномерном движении тела по окружности угловая скорость есть величина постоянная w=const). Промежуток времени, в течение которого материальная точка, двигаясь по окружности, совершает один полный оборот, называют периодом обращения. Период обращения обозначают буквой Т и выражают в секундах.

Величину n, обратную периоду обращения и равную числу оборотов, совершаемых телом за единичное время, называют частотой обращения

n=1/T. (1.29)

Если t=T, угол поворота подвижного радиуса точки равен f=2p. Тогда из (1.28) и (1.29) следует, что

v=2p/Т=2pn. (1.30)

Для точки, равномерно движущейся по окружности радиуса r, линейная скорость

v=s/t, (1.31)

где s - путь, пройденный телом по дуге окружности за промежуток времени t. Угол поворота f выражают в радианах, поэтому f= s/r и

s=rf. (1.32)

Подставив (1.32) в (1.31), получим, согласно формуле (1.28),

v=wr. (1.33)

Формула (1.33) выражает связь между линейной и угловой скоростями равномерного движения по окружности.

Кинематический закон равномерного движения по окружности из формулы (1.28) следует, что f=vt.

Так как при равномерном движении тела по окружности v=const, то из последней формулы для любого момента времени можно найти угол поворота радиуса-вектора, устанавливающего положение точки на окружности. Следовательно, с помощью формулы f=vt можно в любой момент времени найти положение материальной точки, равномерно движущейся по окружности. Это значит, что данная формула выражает собой кинематический закон такого движения (является уравнением этого движения).

Тангенциальное, нормальное и угловое ускорение точки связаны: , где ω - угловая скорость тела.

2.2. Полупроводниковые материалы. Собственные и примесные полупроводники.

Полупроводники - это вещества, удельное сопротивление которых убывает с повышением температуры, наличием примесей, изменением освещенности. По этим свойствам они разительно отличаются от металлов. Обычно к полупроводникам относятся кристаллы, в которых для освобождения электрона требуется энергия не более 1,5—2 эВ. Типичными полупроводниками являются кристаллы германия и кремния, в которых атомы объединены ковалентной связью. Природа этой связи позволяет объяснить указанные выше характерные свойства. При нагревании полупроводников их атомы ионизируются. Освободившиеся электроны не могут быть захвачены соседними атомами, так как все их валентные связи насыщены. Свободные электроны под действием внешнего электрического поля могут перемещаться в кристалле, создавая электронный ток проводимости. Удаление электрона с внешней оболочки одного из атомов в кристаллической решетке приводит к образованию положительного иона. Этот ион может нейтрализоваться, захватив электрон. Далее, в результате переходов электронов от атомов к положительным ионам происходит процесс хаотического перемещения в кристалле места с недостающим электроном — «дырки». Внешне этот процесс хаотического перемещения воспринимается как перемещение положительного заряда. При помещении кристалла в электрическое поле возникает упорядоченное движение «дырок» — дырочный ток проводимости.

В идеальном кристалле ток создается равным количеством электронов и «дырок». Такой тип проводимости называют собственной проводимостью полупроводников. При повышении температуры (или освещенности) собственная проводимость проводников увеличивается.     На проводимость полупроводников большое влияние оказывают примеси. Примеси бывают донорные и акцепторные. Допорная примесь — это примесь с большей валентностью. При добавлении донорной примеси в полупроводнике образуются липшие электроны. Проводимость станет электронной, а полупроводник называют полупроводником n-типа. Например, для кремния с валентностью n — 4 донорной примесью является мышьяк с валентностью n = 5. Каждый атом примеси мышьяка приведет к образованию одного электрона проводимости. Акцепторная примесь — это примесь с меньшей валентностью. При добавлении такой примеси в полупроводнике образуется лишнее количество «дырок». Проводимость будет «дырочной», а полупроводник называют полупроводником р-типа. Например, для кремния акцепторной примесью является индий с валентностью п = 3. Каждый атом индия приведет к образованию лишней «дырки».

2.3. Применение электромагнитной индукции.

Основн.областью явл-ся получение электрич.тока. Рассмотрим процесс на примере генератора. Он представл.собой плоскую рамку, вращ-ся в постоянном магнитном поле. Рамочка вращ-ся с нек.постоянной скоростью 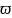. Магнитный ток в любой момент времени равен: Ф=В*S*cos *t. *t-угол поворота в произ.момент времени.

В случае вращения рамки возникает переменная ЭДС. E=B*S*sin *t

Данная ЭДС изм-ся по гармоническому синусоидальному закону. Если рамку замкнуть на нагрузку, в ней будет течь переменный ток.

Пр-с превращения энегрии из механ.и электрич.явл-ся обратимым.

Индукционный ток возникает не только в рамках проводниках, но и массивных проводящих мат-лах, помещенных в электромагн.поле. Данные токи зам-ся внутри массивного проводника и наз-ся токами Фуко. Они также подчиняются правилу Ленца. Взаим-е вихревых токов с переменным магнитным полем приводит к неравномерному распределению мангн.поля по сечению проводника, т.е происодит вытеснение поля на пов-ть. Это явление – скинэффект.

3.1.Основные понятия и величины динамики

В динамике разл.величины хар-ют поступательное и вращательное дв-я.

Поступат.дв-е хар-ют масса, сила и импульс. Масса - мера инертности, хар-щая сопротивление внешних воздействий. Сила – мера возд-я одного тела на другое. Импульс – кол-во дв-я. 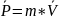, где P-импульс.

Вращательное дв-е хар-ет масса, момент инерции, момент силы и момент импульса.

Момент инерции – величина, численно равная произв-ю массы тел на квадрат расстояния до оси вращения.

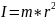
Момент инерции тела определ.конфигурации – сумма моментов инерции отдельных точек для этого тела.

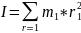
Момент силы – произ-е силы на расстояние до оси вращения. M=F*r

Момент силы, прилож.к определ.конфигурации, равен сумме моментов действующих на все точки тела.

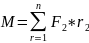
Момент импульса для вращающ.тела – произ-е импульса на расстояние оси вращения.

3.2. Энергетические уровни материалов.

Энергетический уровень — возможные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц, атомных ядер, атомов и т. д.) и подчиняющихся законам квантовой механики. Характеризует определённое состояние системы. Различают электронные и внутриядерные энергетические уровни.