19.Вынужденные колебания. Резонанс.

Вынужденными наз. Колебания возникающие в колеблющейся системе под действием внешней периодической силы. Пусть внешняя вынужденная сила меняется по периодическому закону 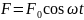. Тогда с учетом силы трения, квазиупругой и вынужденной сил можно записать виде: ;

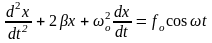(1) ; .

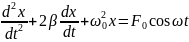
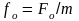Можно убедиться непосредственной проверкой, решение дифф. уравнения затухающих колебаний(ур-ие 1) имеет вид:

(2)

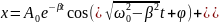
(2) Решение ур-ия (1) складывается из общего решения ур. (1) без правой части( ) и частного решения ур. (1) с правой частью. Из решения (2) вытекает, что для установившегося движения первое слагаемое в (2) обращается в 0 и роль играет только второе слагаемое. Резонанс- резкое возрастание амплитуды вынужденных колебаний при некоторой частоте 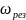. При отсутствии трения (сопротивления) рез. частота совпадает с собственной частотой ω.

;

;

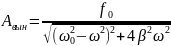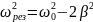из этой формулы вытекает, что при отсутствии трения, когда , резонансная амплитуда устремляется в , а резонансная частота совпадает с собственной частотой .

Рассмотрим резонанс вынужденных колебаний с учетом квазиупругой и вынужденной сил, но без учета трения: ; будем искать решение последнего ур-ия виде: ; ; ; ( ) ; ; ;

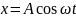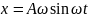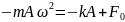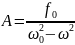
Е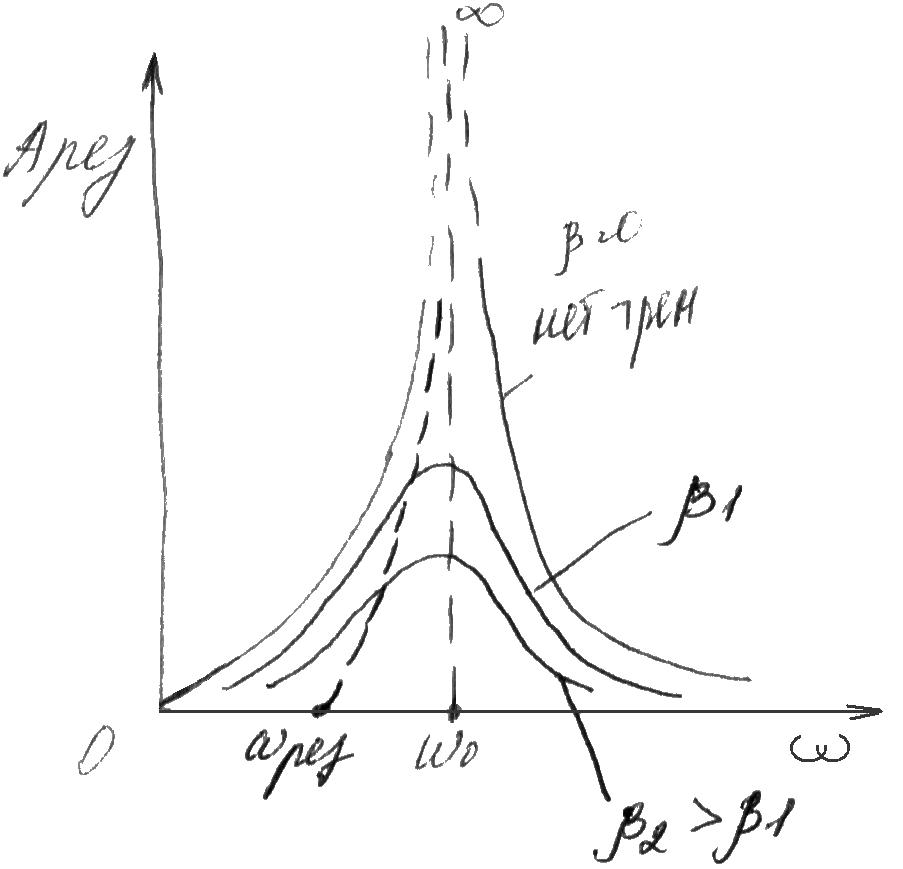 сли , то .

20.Упругие волны в средах.

В олна –процесс распространения колебаний в среде. Для распространения волны необходим источник волны. Волны в среде распространяется с некоторой скоростью 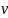. При распространении волны в среде частицы не переносятся с волной, а совершают колебания возле положения равновесия. Механические или упругие волны представляют собой процесс распространения возмущений в упругой среде. Различают волны продольные и поперечные. Волна продольная если колебания частиц среды происходит вдоль распространения волны. Волна поперечная если колебание частиц происходит в направлении перпендикулярном направлению распространения волны. Продольные волны могут распространяться во всех средах (газ, жидкость, твердые тела) при диффузии сжатия и растяжения. Поперечные – только в твердых телах, при диффузиях сдвига. Упругая волна наз. Синусоид-но гармонической если колебания частиц среды гармонические. 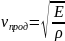(E-модуль Юнга,

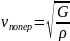
(G-модуль сдвига) ; . Фронт волны - геометрическое место точек до которых дошли колебания. Волновая поверхность- совокупность точек колеблющихся в одной фазе.

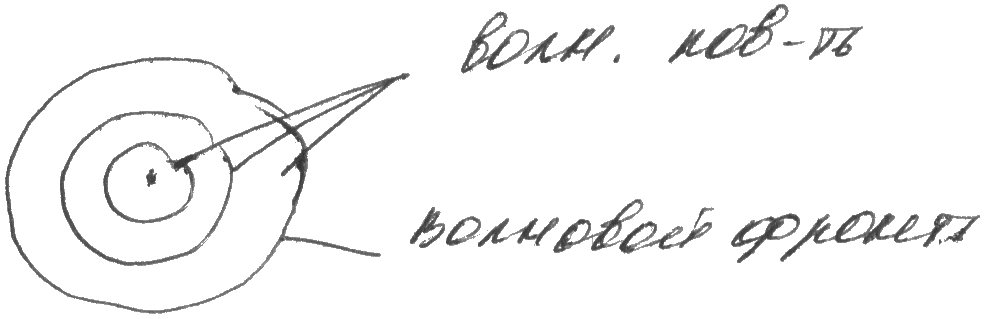
21О.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.

Бегущими наз-тся волны(в.), кот-ые переносят энергию в пр-стве.

Ур-ние в. наз-тся выр-ние, задающее смещение колеб-хся частиц, как ф-цию корд-т xyz и времени t.

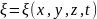
Найдём ур-ние поперечной одномерной плоской бегущей волны.

Волна плоская, если фронт плоский.

П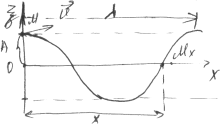 усть т.М колеблется в упругой среде вдоль оси 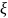около положения равн-сия по гарм-ому закону, т.е.

Т.к. среда упр-ая, то кол-ния т.М будут перед-ся соседним т. среды и вдоль оси х будет распр-ся поперечная среда. В т.М_х с координатой х дойдут с запаздыванием по времени

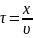
Если кол-ния т.М незатух-щие, то т.М_х будет кол-тся с такой же частотой и амплитудой А, но с запаздыванием по времени на

Если учесть нач-ую фазу

В ур-ии волны -смещение частиц среды от пол-ния равновесия.

А – амплитуда (по опред-ию +) наибольшее смещение частиц среды от положения равн-сия.

– циклическая частота.

Х – расстояние от источника волны до точки, в кот-ой рассматр-тся смещ-ие

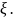
t – текущее время, начало отсчёта которого опред-тся начальной фазой

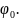
Гребнями волны наз-ся максимальные точки смещения.

Впадины – это – А.

Фаза в. – выр-ние, стоящее под cos.

Ур-ние (*) есть ур-ние в., распред-щейся вдоль полож-го напр-ния оси х.

- в отриц-ом напр-ии

Длина в. – расст-ие между частицами среды, для кот-ых разность фаз =2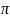 ,т.е. с учётом сказанного имеем

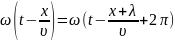
или

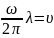
-число кол-ний

Период кол-ий – время, за кот-ое частица среды сов-ет полное кол-ие

;

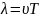
Длина в. – расст-ие , на кот-ое распр-тся опр-ая фаза кол-ия, за время = периоду.

За период Т в. распр-тся на свою длину .

Запишем др. выраж-ия для ур-ия в.

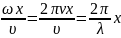
Волн-ое число – число, уклад-щееся в 2 .

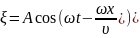
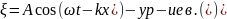
Ур-ие в. можно записать в других видах:

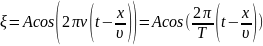
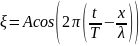
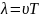
В комплексном виде

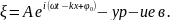
Ур-ие сфер-ой в.

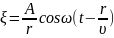
Пусть при волн-ом процессе фаза постоянна, т.е.

Продифф-ем

;

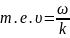
Фазовая скорость зависит от частоты.

Среда, в кот-ой наблюд-тся завис-сть фаз.ск. в. от её частоты, наз-тся дисперсной.

Дисперсия- разложение белого цвета в спектр при прохождении света через стекл-ую призму.