12О. Движение тела переменной массы.

Получим уравнение движения ракеты (уравнение Мещерского):

Масса ракеты m меняется со временем. Пусть момент времени t, скорость и масса m. По истечении времени dt, масса ракеты уменьшится и станет (m - dm), где dm – масса сгоревшего топлива, скорость возрастёт и станет 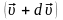, _отн – скорость истекающе-сгорающего топлива относительно ракеты.

Изменение импульса системы равно конечному импульсу минус начальный импульс m .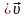

ракета топливо

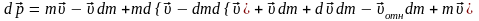
|| : dt

- уравнение Мещерского

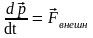- сила действия на ракету

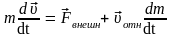- уравнение Мещерского

Спроектируем уравнение Мещерского на направление движения ракеты, тогда получим :

= 0

|| :

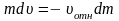Проинтегрируем :

, = const

Или спотенцируем :

Пусть в момент времени t = 0, скорость ракеты равна 0 , а масса m₀ :

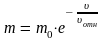- формула Циолковского

Для химического топлива скорость сгорания : = 4 км/с

Первая космическая скорость : = 8 км/с

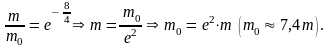
13О. Кинематика гарманических колебаний

Колебание – движение или процессы отличающиеся повторяемостью во времени. Колебания физич-ой велечины х называются гарманическими, если она изменяется со временем по з-ну cos или sin, т.е.:

х = Аcos(ωt + φ_o)

A > 0 – амплитуда – максимальное значение колеблющейся величины х.

ω – круговая, угловая, циклическая частота.

t – текущее время (начало отсчёта времени определяет φ_o – начальная фаза).

(ωt + φ_o) – фаза гарманических колебаний.

При заданной амплитуде А фаза однозначно определяет велечину х.

Начальная фаза и фаза измеряются в рад.

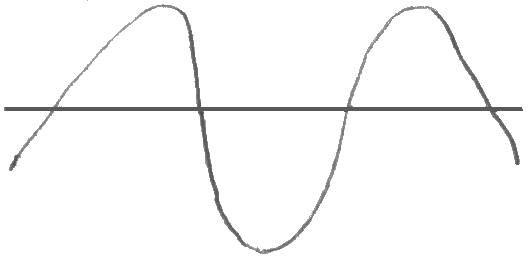- А≤ х ≤ А

Т – период колебаний – промежуток времени, по истечении которого колебания повторяются, а фаза получает приращение 2π.

ω(t + Т) + φ_o = ωt + φ_o + 2π

ωТ = 2π

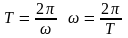
Величина обратная периоду:

ν = 1/Т – частота колебаний – число колебаний за единицу времени.

[ν] = Гц (герц)

ГК графически изображаются методом вращения вектора амплитуды или иначе методом векторных диаграмм.

Пусть тМ вращается по окружности радиуса А с постоянной угловой скоростью ω:

Коор-ты тМ меняются по гармоническому з-ну: х = Аcos(ωt + φ_o).

14О. Гармонический осциллятор.

Получим дифференциальное уравнение описывающее систему совершающую ГК. Для этого вычислим 1-ую и 2-ую производные по времени от ГК величины х:

(1) х = Аcos(ωt + φ_o)

(2)

(3)

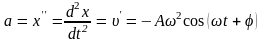
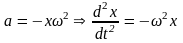
(*) - уравнение гармонического осциллятора.

Система, поведение которой описывает выражение (*) наз-ся гармоническим осциллятором.

Решением уравнения (*) является выражение:

х = Аcos(ωt + φ_o)

Покажем, что на тело совершающее ГК действует квазиупругая сила описываемая з-ном Гука:

F = - kx

F = ma

a из (3): F = - m = - kx, где k = m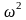

Найдём полную механическую энергию гармонического осциллятора:

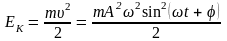
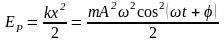
- з-н сохранения энергии для гармонического осциллятора.

Энергия ГК величины пропорциональна квадрату амплитуды: E ~ А²

Гармонический осциллятор является маятником.

15О. Примеры гармонических осцилляторов.

Маятники: пружинный, математический, физический.

Пружинный маятник – тело с массой m соединённое с пружиной и совершает колебания при выведении из положения равновесия при действии силы Гука.

F _упр = - kx

По II-му з-ну Ньютона имеем уравнение движения этого маятника:

ma = F

m = - kx || : m ;

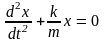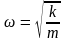
х = Аcos(ωt + φ_o)

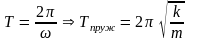
Математический маятник – математическая точка (m), подвешенная на невесомой нерастяжимой нити длиною l и совершает колебания под действием силы тяжести при выведении точки из положения равновесия.

О сновное уравнение динамики вращательного движения для математического маятника.

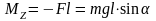
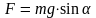
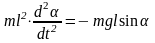|| : l

(1)

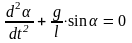
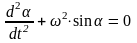
(1) уравнение колебаний математического маятника, если α – мало, то 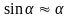(рад)

α ≤ 10⁰ ≈ 0,17 рад

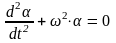- уравнение колебаний математического маятника.

Малые колебания математического маятника гармонические.

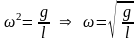α = α_о cos(ωt + φ_o)

Если колебания не малые, то разлагая sin в ряд, получаем:

Получим из (1) уравнение не линейных колебаний:

Ф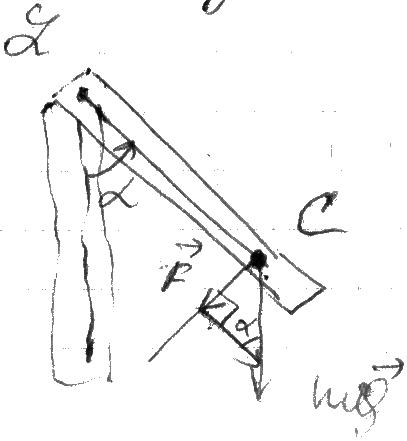 изический маятник – твёрдое тело, совершающее колебания под действием силы тяжести вокруг оси, не проходящей через центр тяжести.

Получим уравнение, описывающее колебания физического маятника:

ZC = l (от точки подвеса до центра тяжести)

Уравнение движения:

(α в рад)

Малые колебания гармонические.