9О. Потенциальная энергия системы.

Е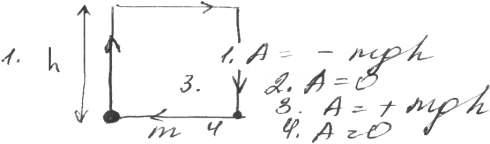 _р обусловлена взаимным расположение тел системы, их конфигурацией и характером взаим-вия тел. Е_р можно ввести только для консервативных сил. Сила, дейст-щая на тело наз-тся конс-ной, а поле этой силы потенц-ым, если работа этой силы не зависит от формы траектории, по кот-ой тело перешло из одного сост-ния в другое, а зависит только от нач-го и кон-го полож-ния тела.Работа конс-ной силы не зависит от пути. Сила наз-тся конс-ной, если её работа по замк-той траект-ии =0.

Конс-ми силами явл-тся:

F_G-гравитационная ; F_кулона ; F_{упругости}

А_{рез-щая}= - mgh +0 +0+ + mgh=0

Сила наз-тся неконс-ной, если работа этой силы зависит от пути.

Неконс-ми явл-тся:

-трения -сопротивления -диссипативные

П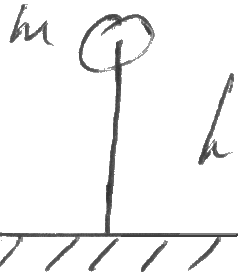 окажем, что А F_тр не конс-на. Работа F_тр <0 и поэтому по замкнутой траект-ии отлична от нуля.

А_тр= <0

Рассм-им примеры:

1. Е_ртела массы m поднятого на h

А= - mgh

A = - E_p

Работа сов-тся за счёт убывания пот-ной энергии Е_р= mgh

2 . E_p упругодеф-го тела (пружина)

А= F_упрdx F_упр= - kx A= -kxdx dE_p=kxdx

Проинтегрируем

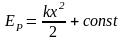; = 0

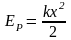; = 0, тк предпологаем, что E_p недеформировонного тела = о. E_p не зависит от выбора СО, а зависит от выбора нулевого уровня отсчёта энергии. Начальный уровень отсчёта энергии не влияет, поскольку в задачу входит разность ∆E_p.

3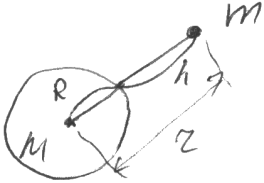 . Покажем, что энергия гравитации взаимодействует отрицательно.

r = R + h ; h << R

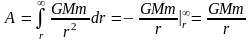
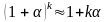; α – мало, α ≈ 0. α = h/k; k = -1

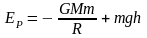
В ядрах атома отрицательная потенциальная энергия взаимодействия протонов и нейтронов приводит к дефекту масс. Теория относительной потенциальной энергии теряет смысл, тк предполагается бесконечная скорость взаимодействия.

10. Закон сохранения энергии в механике

Рассмотрим с-му n мат. точек. Пусть m_i, v_i соответственно масса и скорость. Пусть на i-ю точку со стороны k-ой действует внутренняя консервативная сила f_ik. Пусть F_i - равнодействующая внешних консервативных сил, и F_i^* - это равнод-я внешних неконсервативных сил на i-ю точку.

По 2-му закону Ньютона имеем ур-е дв-я с-мы:

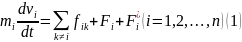
Умножим обе части ур-я (1) на выр-е v_idt=dr_i, и просуммируем по всем точкам с-мы:

Выр-е слева в ф-ле (2) – это и есть изменение E_k. 1-е слагаемое справа в (2) есть работа внутр. консервативных сил и она равна убыли E_p взаимодействия:

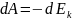
2-е слагаемое в (2) есть работа внеш. консерват. сил и она равна убыли E_p c-мы во внешнем поле с-мы. Последнее слагаемое в (2) есть работа на с-мой внеш. неконсерв. сил. С учетом вышесказанного:

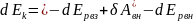
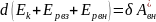
Пусть внешних сил нет:

d( )=0

– закон сохранения энергии (зсэ)

Полная мех. энергия замкнутой консерват. с-мы тел, на кот. действуют лишь консерв. силы, остается постоянной. ЗСЭ – общефизический закон.

ЗСЭ связан с однородностью времени, т.е. симметрии по отношению к сдвигу времени. Однородность времени не означает независимость закона физ. явлений от выбора начала отсчета времени. Такая инвариантность относительно сдвига времени означает ненаблюдаемость абсол. времени.

11О. Закон сохранения момента импульса.

Пусть твёрдое тело вращается вокруг неподвижной оси Z, тогда элементарная работа всех внешних сил равна приращению Е_К вращающегося тела (по з-ну сохранения Е), т.е.:

dA = dE_K

dA = M_Z*dφ

E_K = I_z*ω²/2 ; I_z = const

M_Z*dφ = I_z*ωdω || : dt

M_Z*(dφ/ dt) = I_z*ω(dω/dt)

M_Z = I_z*(dω/dt)

M_Z = d(I_z*ω)/dt

M_Z = dL_Z/dt

Пусть внешних сил нет, тогда M_Z = 0, поскольку моменты внутренних сил (3-ий з-н Ньютона) взаимно скомпенсированы :

M_Z = 0 ; dL_Z/dt = 0 ; L_Z = const (з-н сохранения момента импульса).

Суммарный момент импульсов замкнутой системы тел (частиц) сохраняется.

I₁*ω₁ = I₂*ω₂

З-н сохранения импульса связан с изотропностью пространства, т.е. симметричностью пространства, означает равноправие всех пространственных направлений.

Поворот в изотропной системе пространства как целого не меняет свойств системы и з-нов её движения.