7О. Закон сохранения импульса.
Рассмотрим систему мат-ых т. , сост-щую из n точек. Силы, действующие между т-ми системы наз-ся внутренними. Прочие – внешними.
Система наз-тся замкнутой (изолированной) если отсутствуют внешние силы.
Пусть
на i-ую точку системы
действуют внешние силы с равнодействующей
и внутренней силой
.
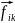По 2-му з.Ньютона имеем ур-ие дв-ния для m мат-ых точек.
=
mi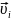
k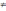
i
означает, что нет самодействия
=
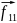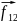=….=0
Проссумируем ур-ие 1 по всем точкам системы.
Слагаемое
= 0, т.к. по 3 з. Ньютона
=
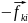
Поэтому
в сумме (3)
=
;
=
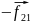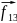и т. д. поэтому она =о
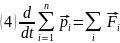
Импульсом системы тел (точек) наз-тся векторная сумма импульсов отдельных точек системы.
Закон изменения импульсов системы
Производная по времени от вектора импульса системы точек (тел) равна вект-ой сумме всех внешних сил, приложенных к системе.
Если
внешних сил нет (
=0),
то
=0,
тогда
=соnst.
З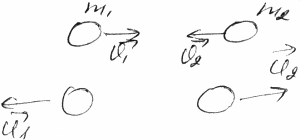
акон
сохранения импульса системы : импульс
замкнутой системы мат-ых точек (тел)
сохраняется.
m1
1+
m2
2+….=
m1
1+
m1
1+….
З
СИ
применим также в теории относительности
ЗСИ связан с однородностью пространства, т.е. симметрии законам физики по отношению к пространственным сдвигам начала координат (по отн-ию к трансляциям).
В однородном пр-стве перенос замкнутой системы как целого не меняет законов дв-ния системы. Пустое пр-ство однородно.
Покажем теперь, что поступ-ое дв-ние тела можно заменить дв-ем центра масс тела, т.е. дв-ем одной точки. Пусть тело массой М поступ-но движется со скоростью . Радиус-вектор центра масс тела
mi – масса i-ой частицы тела
ri – радиус-вектор i-ой частицы
Продифф-ем
rc
по t
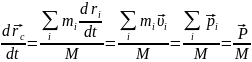
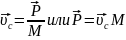
Возьмем производную
8О. Работа.Мощность.Кинетическая энергия системы.
Е
– энергия. Энергия системы есть
универсальная мера различных форм
дв-ния. Она хар-ет спос-сть системы тел
совершать работу и измеряется этой
работой.
Элем-ой
работой dA
переменной силы
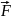на перемещение
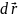наз-тся скал-ое произв-ие силы и
перемещения.
dA=(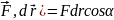
Поскольку
d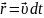
,
то
dA=(
Конечная работа при перемещении тела из положения 1 в пол-ие 2 есть криволин-ый интеграл.
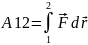
Рассмотрим частные случаи:
1.пусть сила F=const, траект-ия – прямая, напр-ие силы совп-ет с напр-ем перем-ия и тело проходит путь S.
A=FS
[A]=1Hм=1Дж
2.Сила
перем-ия
cos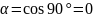
след-но A=0
Сила,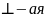
перем-ию, работы не совершает
3.работа силы трения всегда отрицательна
А
=FтрScos180
=-FтрS
В
ычислим
работу тела (точки) вращ-гося по окр-ти
радиуса R.
dA=dSF=FRd
=Mzd
dS=Rd ([d ]=1 рад)
dA=Mzd
Интегрируем
Скорость совершения работы хар-ет мощность-есть произв-ая от работы по времени.
;
;
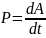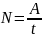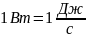[P]=1Вт
P=1 Вт если за 1 сек сов-тся работа в 1 Дж.
dA=(
,
след-но N=
=F
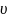cos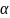
Полная мех-ая энергия Е складыв-тся из кин-ой Ек и пот-ой Ер.
Кинет-ая эн-ия обусл-на дв-ем тела и изм-тся работой, кто-ую тело может сов-ть при торможении его до полной остановки, т.е. dEk=dA.
Получим выр-ие для Ек для поступ-го дв-ия:
m-масса тела, движ-ся со ск-тью под действием нек-ой силы F
dA=FdS
По 2 з.Ньютона имеем
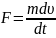
Проинт-ем обе части получ-го выр-ния
m=const
Const=0,
т.к. считаем, что при отсутствии
P=m
Кин-ая энергия системы тел (точек) по опр-ию равна сумме кин-их эн-гий отд-ых частиц, т.е.
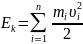
Н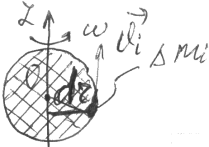
айдём
Ек
тела, вращ-гося с угл-ой ск-тью
вокуг оси z.
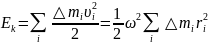
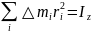
Если
тело массой М движется пост-но со
скоростью
(центра масс, инерции) и одновр-о вращ-тся
с
вокруг оси, прох-щей через центр масс,
то
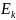тела склад-тся из
пост-го и вращ-го дв-ния, т.е.
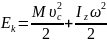
-зависит от выбора системы отсчёта, т.к. от сист-ы отс-та зависит .