
- •1О. Кинематика поступательного движения.
- •2О. Кинематика вращательного движения.
- •3О. Динамика частиц. Закон ньютона.
- •4О. Неинерциальные системы отсчета (нсо). Силы инерции.
- •5О. Основное ур-ние динамики вращательного движения тв. Тела.
- •7О. Закон сохранения импульса.
- •8О. Работа.Мощность.Кинетическая энергия системы.
- •9О. Потенциальная энергия системы.
- •10. Закон сохранения энергии в механике
- •11О. Закон сохранения момента импульса.
- •12О. Движение тела переменной массы.
- •13О. Кинематика гарманических колебаний
- •14О. Гармонический осциллятор.
- •15О. Примеры гармонических осцилляторов.
- •16. Сложение гармонических колебаний одного направления и частоты.
- •17. Сложение взаимно перпендикулярных гармонических колебаний.
- •18. Затухающие колебания.
- •19.Вынужденные колебания. Резонанс.
- •20.Упругие волны в средах.
- •21О.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.
- •22. Одномерное волновое ур-е. Энергия волны.
- •23. Распространение волн в средах с дисперсией. Групповая скорость, ее связь с фазовой скоростью.
- •24. Стоячие волны
- •25. Элементы акустики.
- •26.Модуль Юнга. Скорость звука.
- •28. Постулаты сто. Преобразование
- •29. Средства преобразования Лоренца.
- •30. Релятивистский закон сложения скоростей.
- •31. Интервал между событиями и его инвариантность в преобразовании Лоренца
- •32. Релятивистская динамика, кинетическая энергия сто.
- •33. Связь массы, энергии, импульса в сто
- •34О. Эффект Доплера
- •35О. Принцип эквиваленности.Понятие о ото
- •36О. Равновесие и течение жидкости и газа
- •37О. Уравнение неразрывности струи. Уравнение Бернулли
- •38. Уравнение Эйлера. Движение идеальной жидкости.
- •39. Течение вязкой жидкости. Формула Стокса.
- •40. Течение вязкой жидкости в трубах. Формула Пуазейля.
- •41. Динамический и статистический закономерности в физике.
- •42. Уравнение состояния идеального газа.
- •43. Основное уравнение молекулярно-кинетической теории газов (мкт).
- •44. Молекулярно-кинетический смысл абсолютной температуры.
- •45. Распределение Максвелла.
- •46. Параметрическая формула распределения Больцмана.
- •47. Распределение Гиббса.
- •48. Первое начало термодинамики.
- •49. Теплоемкость многоатомных газов.
- •50. Применение I начала термодинамики к изопроцессам(термодинамическим процессам).
- •51. Адиабатический процесс.
- •52. Политропный процесс
- •53. Теплоемкость и работа газа в политропном процессе
- •54. Обратимые и необратимые процессы, круговой процесс, тепловые двигатели, холодильные машины.
- •55. Цикл Карно. Максимальный кпд тепловой машины.
- •56. Технические циклы.
- •57. Второе начало термодинамики (6 формулировок).
- •58. Энтропия
- •59.Принцип возрастания энтропии
- •60. Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.
- •61. Метод термодинамических потенциалов (характеристических функций).
- •62. Явления переноса. Средняя длина свободного пробега молекул.
- •63. Коэффициент диффузии.
- •64. Теплопроводность. Коэффициент теплопроводности.
- •65. Уравнение теплопроводности.
- •66. Вязкость. Коэффициент вязкости.
- •67. Фазовые равновесия и превращения. Фазы и фазовые превращения.
- •68. Уравнение Клайперона - Клаузиса.
- •69. Реальные газы. Уравнение Ван – дер - Вальса .
- •70. Изотермы Ван-дер-Ваальса. Критич. Состояние. Внутр. Энергия реального газа.
- •71. Твёрдые тела.Теплоёмкость кристалла
- •72. Жидкости.Поверхн. Натяж. Жидк.
- •73. Смачивание и капиллярные явления
- •74. Принцип динамич. Отопления
- •75. Элементы физики полимеров
- •1О. Кинематика поступательного движения.
4О. Неинерциальные системы отсчета (нсо). Силы инерции.
Основное уравнение динамики в форме F = ma справедливо только в инерциальной системе отсчета. Рассмотрим уравнение движения тела в НСО, т.е. в системах, которые движутся с ускорением. Будем считать, что все скорости движения много меньше скорости света. При движении тела в НСО возникают следующие силы инерции, действующие на тело:
1) Поступательная сила инерции при ускоренном поступательном движении НСО.
2) Центробежная сила инерции, действующая на покоящееся или движущееся тело во вращающейся системе отсчета с постоянной угловой скоростью.
3) Сила Кориолиса – сила действующая только на движущееся тело во вращающейся системе отсчета.
4) Сила инерции- обусловленная неравномерностью вращения системы отсчета. β =dw/dt ≠ 0
В![]() се
силы инерции пропорциональны массе
тела и потому по своим свойствам
аналогичны силам тяготения. Тогда
локально справедлив принцип эквивалентности
сил инерции и гравитации с учетом
равенства инертных и гравитационных
масс.
се
силы инерции пропорциональны массе
тела и потому по своим свойствам
аналогичны силам тяготения. Тогда
локально справедлив принцип эквивалентности
сил инерции и гравитации с учетом
равенства инертных и гравитационных
масс.

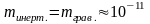
С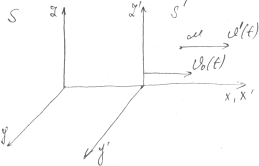 илы
инерции не подчиняются 3 з-ну Ньютона о
равенстве действия или противодействия
поскольку нет противоположной силы
приложенной к другому телу. Силы инерции
не подчиняются, т.е. меняются при переходе
от одной установленной системы отсчета
к другой.
илы
инерции не подчиняются 3 з-ну Ньютона о
равенстве действия или противодействия
поскольку нет противоположной силы
приложенной к другому телу. Силы инерции
не подчиняются, т.е. меняются при переходе
от одной установленной системы отсчета
к другой.
1)Рассмотрим силу инерции при поступательном ускоренном движении системы отсчета
Пусть система S' движется ускоренно относительно неподвижной инерциальной системы S вдоль оси х со скоростью υ(t). Пусть тело (точка) М движется относительно системы S' со скоростью υ' (t). Тогда по теории сложения скоростей скорость = о + '. Продифференцируем по t последнее выражение:
ā = āо + ā' || *m (масса)
m ā = m āо + m ā' m ā' = m ā - māо m ā' = F + Fn
2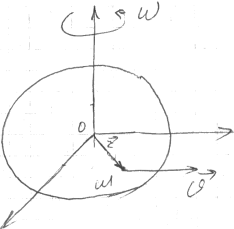 )
На покоящееся или движущееся тело во
вращающейся системе отсчета с угловой
скоростью ω действует центробежная
сила инерции. Она равна :
)
На покоящееся или движущееся тело во
вращающейся системе отсчета с угловой
скоростью ω действует центробежная
сила инерции. Она равна :
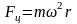
Направлена по радиусу от 0 (центра окружности). Действие этой силы используется в центрофугах, центробежных насосах. Наличие Fц приводит к различию на земле силы тяжести и силы тяготения.
3) Сила Кориолиса или переносная сила инерции.
Она
возникает во вращ. Сист. Отсчета только
при движении со скоростью
’
(На покоющ. тело эта сила не действует)

Эта сила обращается в 0 если ’=0 или ’|| ω
Эта сила не меняет модуль скорости поэтому не совершает работы. В северном полушарии сила кореолиса приводит к размыванию правого по теч берега рек. Приводит к отклонению падающ тел к востоку.
4)
Если система вращается неравномерно
 ,
то возникает 4ая сила инерции, равная
,
то возникает 4ая сила инерции, равная

Окончательно уравн. движения тела во вращ сист отсчета имеет вид

При ускоренном, поступ и вращ движении НСО уравн имеет вид

5О. Основное ур-ние динамики вращательного движения тв. Тела.
А бсолютно
твердым называется тело у которого во
время движения не
меняется взаимное положении частей.
бсолютно
твердым называется тело у которого во
время движения не
меняется взаимное положении частей.
Введем предварительные понятия.
Определение: Моментом М силы относительно точки О называемой полюсом или началом, называется векторное произведение радиуса вектора на силу .
 =[
,
]
=[
,
]
Момент силы перпендикулярен плоскости в которой лежат векторы и .
M=rFsinα [M]=H*м
Н![]() аправление
М опр-тся правилом векторного произв:
«Если вращать от
к
на
кратчайший угол, то то винт укажет
направление
».
M=F*d
аправление
М опр-тся правилом векторного произв:
«Если вращать от
к
на
кратчайший угол, то то винт укажет
направление
».
M=F*d
Определение: Моментом импульса L называется векторное произведение радиуса вектора r на импульс точки Р: L=[r,P] продиф. по t
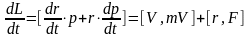
 (1)
(1)
О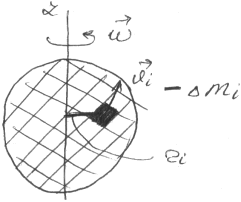 бобщим
теперь уравнение (1) на случай тела,
вращающегося с угловой скоростью ω,
вокруг фиксированной в пространстве
оси z.
бобщим
теперь уравнение (1) на случай тела,
вращающегося с угловой скоростью ω,
вокруг фиксированной в пространстве
оси z.
.
Разобьем тело на малые частицы с массами

Спроецируем ур-ние (1) на z:
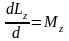 (2)
;
(2)
;
 (3)
(3)
Просуммируем ур-ние (3) по всем частицам.
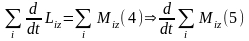
Моментом
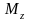 ,
отн. оси z
называется сумма моментов импульсов
отдельных частиц тела относительно
этой оси. т.е.
,
отн. оси z
называется сумма моментов импульсов
отдельных частиц тела относительно
этой оси. т.е.
 (6)
(6)
Моментом
силы
,
действ. на тело относительно оси z,
наз. сумма проекций моментов сил,
действующих на отд. частицы тела. Т.е.
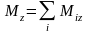 (7)
(7)
Тогда с учетом (6) и (7) ур-ние (5) приобретает вид:
 (8)
– основное ур-ние динамики вращ. движения.
(8)
– основное ур-ние динамики вращ. движения.
(8) Производная по времени от момента импульса тела, относительно неподвижной оси вращения равна результирующему моменту всех сил, действующих на тело, относительно этой оси вращения.
Получим другие формы уравнения (8)
Из
рис 1 имеем:
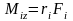
Момент
силы относительно оси z
равен произведению силы
 на плечо
на плечо

П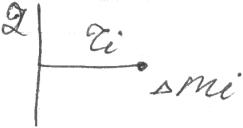 лечо
- длина перпендикуляра, опущенного из
оси z
на линию действия силы.
лечо
- длина перпендикуляра, опущенного из
оси z
на линию действия силы.
 ,
тогда
,
тогда

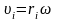
Момент инерции тела, относительно оси z вращ. с угл. скоростью ω равен произв. Iz и ω
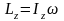 (10) ;
(10) ;
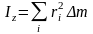 (9)
(9)
Момент
инерции точки с массой
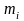 отн. оси Z
равен произведению массы этой точки на
квадрат расстояния до оси.
отн. оси Z
равен произведению массы этой точки на
квадрат расстояния до оси.
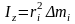
Момент инерции из (9) есть сумма моментов инерции частиц составляющих тело.

Уравнение
(8) с учетом (10) приобретает вид :
 (11)
(11)
Если
Iz=const,
то
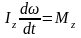 (12)
Т.к.
(12)
Т.к.
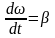 ,
то
,
то
 (13)
(13)
(13) : Момент силы отн. оси вращения Z равен произведению момента инерции тела отн. этой оси на угловое ускорение тела β.
Еденицы
измерения момента инерции : [Iz]=кг*м^2
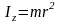
Момент инерции тела играет роль массы во вращ. движении.
Момент инерции тела. Теорема Штейнера.
I![]() zi=
zi= mi*zi2
mi*zi2
Iz=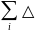 mi*zi2
mi*zi2
Момент
инерции тела отн-но некот-ой оси есть
сумма моментов инерции отдельных частиц
, сост-щих это тело. В пределе, когда
число разбиений
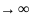 :
:
Iz=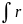 2dm
2dm
где суммирование ведётся по всей массе тела.
dm= dV
dV
Iz= 2dxdydz
r2=x2+y2+z2
2dxdydz
r2=x2+y2+z2
Сопоставим ур-ие дв-ния поступ-го и вращ-го дв-ния.
Fs=ms*as
Mz=Iz*
Момент инерции тела во вращ-ом дв-нии аналогичен массе в пост-ом дв-нии. Т.е. момент инерции тела есть мера инертности тела во вращ-ом дв-нии.
Масса-мера инертности тела в пост-ом дв-нии. Инертность – cв-во тела сохр-ть сост-ие покоя или равно-го прямолин-го дв-ния в отсутствии действия сил. Во вращ-ом дв-нии если тело имеет большой момент инерции, то тело стрем-ся сохр-ть сост-ие покоя или равном-го вращения.
Рассмотрим моменты инерции тел в простейших случаях.
1.момент инерции точки массы m на раст-нии r от оси есть величина
Iz=mr2 [Iz]=кг*м2
2. момент ин-ции однородного кольца или полого цилиндра Iz=mr2
3.
диск или сплошной цилиндр Iz= mr2
mr2
4.
момент инерции шара Iz=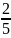 mr2
mr2
5. момент инерции стержня
![]() Iz=
Iz=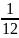 ml2
ml2
6. момент инерции стержня отн-но оси, прох-щей через его конец
![]() Iz=
Iz=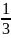 ml2
ml2
Момент инерции тела не зависит от вращения тела. Зависит от формы тела, его размеров, распределения плотности массы в теле и от выбора оси.
Центром инерции тела (центром масс, центром тяжести) наз-тся т. с радиус-вектором
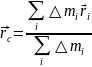
где суммир-ние ведётся по всем частицам тела.
 ri
-радиус
вектора i-ой
частицы
ri
-радиус
вектора i-ой
частицы
В проекции на координатные оси имеем

Т-ма
Штейнера: момент инерции тела отн-но
оси z
равен моменту ин-ции тела отн-но -ой
оси zc
, прох-щей через центр инерции тела,
сложенному с произв-ем массы тела m
на квадрат расст-ия d
между осями.
-ой
оси zc
, прох-щей через центр инерции тела,
сложенному с произв-ем массы тела m
на квадрат расст-ия d
между осями.
Iz=Izc+md2
Д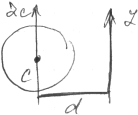
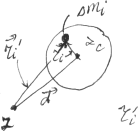 ок-во:
пусть ось z
неподвижна так, что траект-ии всех частиц
тела лежат в
ок-во:
пусть ось z
неподвижна так, что траект-ии всех частиц
тела лежат в
 пл-стях. Ось z
проходит через центр тела. Расст-ие
между осями d.
пл-стях. Ось z
проходит через центр тела. Расст-ие
между осями d.
Из
рисунка
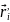 =
= +
+
Возведём 2 этих части в квадрат
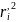 =
= +d2+2
+d2+2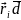
Домножим
обе части на
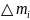 и просуммируем по всем элементам тела
и просуммируем по всем элементам тела

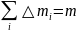
 (по определению
радиус-вектора центра инерции)
(по определению
радиус-вектора центра инерции)
Iz=Izc+md2
Ч.Т.Д.
