71. Твёрдые тела.Теплоёмкость кристалла
Тв.
тела отлич. от газообр. и жидкю постоянством
формы, V. Они делятся на кристаллич. и
аморфные.Большее число тв. тел кристалл-кие.
Для кристаллов харак-но наличие
кристаллич. решётки. Кристалл как правило
проявл. анизотропные физ. св-ва (разные
по разным направл.) Аморфные тела –
переохлажд. жидкости(стекло, смола,
битум). Они проявл. изотропные св-ва.
Вычислим теплоёмк. кристалла.Т.к. V тв.
тел маломеняется, то теплоёмк Cp
и CV
примерно
одинаковы и можно говорить просто о
теплоёмкости С. Внутр. энергия крист.
решётки тв. тела сост. из кинетич. и
потенц. энергии атомов и ионов в узлах
этой решётки. При этом на кажд. степ.
свободы приход-ся
kT
в виде кинетич. энергии и
kT
в виде потенц. энергии.
kT+
kT=kT.
Т.к. атом имеет 3 степ. свободы, то энергия
атома будет 3kT.
Так как 1 моль содерж NА
атомов, то внутр. энергия U= NА
3kT=3RT.
Теплоёмкость
С=
=
+
(
=0);
C=3R
≈25
З-н Дюлонга и Пти (1815). «Молярн. теплоёмк. кристаллич. атомарных тел одинакова и равна 3R».
П
ри
низк. темпер. наблюд. отклонение от з-на
Дюл. и Пти, при этом происх. постеп.
«вымерзание» колебательн. степеней
свободы.При низк. темп. теплоёмк. мен-ся
по з-ну С= const∙
(з-н
П.Дебая)
На графике з-н Дебая им. вид:
72. Жидкости.Поверхн. Натяж. Жидк.
Различают. тв., жидк. и газообр. состоян. вещ-ва.Они связаны с постоянством формы и V тела. Ф.Каменецкий считал, что плазма–4-ое состоян. вещ-ва.5-ое сост. – жидкокристаллическое(ЖК) пример–жидкие кристаллы. Жидк. состоян. вещ-ва заним. промеж. состоян. между газообр. и кристалл-ким. Для жидк. как и для тв. тел хар-но налич. определ. объёма. Но жидк. подобно газу заним. форму сосуда, в кот. она наход-ся. Жидк. слабосжим. Молекулярн. давление для них доходит до р*=20000атм. В расположении частей жидк-ти наблюд. ближн. порядок, т.е. по отнош. к люб. частице жидк-ти расположение соседн. частиц явл. упорядоченным, а далее упорядочен-ть быстро убыв. В жидк. из-за отсутсвия дальнего порядка обычно не проявл. анизотропные св-ва, однако это не относ-ся к жидк.кристаллам и анизотропн. жидк-тям. Силы взаимод. между молекулами жидк. играют большую роль, чем в газах. В поверхн. слое жидк-ти обнаружив-ся нескомпенсиров. межмолекулярн сил.Частицы жидк. в этом случае испыт. силу притяж. со стор. друг частиц, направл. внутрь жидк-ти.
П
ереход
молекулы из глубины жидк-ти в поверхн.
слой связан с работой против действ-щих
в поверх. слое сил. На эту работу молекула
тратит часть своей кинетич. энерг.,но
зато приобрет. потенц. энергию. Из-за
наличия поверх-ной энергии жидк-ть ведёт
себя,как если бы она заключалась в
упругую растянутую плёнку, кот. стрем-ся
сжаться. Рассм. проволочн. каркас,
затянутый мыльной жидкостью (мыльный
пузырь).
Чтобы
удержать жидк-ть в равновесии надо
прилож. силу
к линии свободн. границы
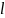.Эта
сила лежит в пл-ти плёнки и направл. по
нормали к линии границы плёнки. Опыт
показыв.,что
поверхн-го натяж. пропорц
.
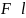; F=α
(α-коэффиц. поверхн. натяж. зависит от
рода жидк-ти и темпер.)
1.
α=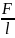
.
Коэффиц. поверхн. натяж. α численно равен
силе, прилож. к единице длины края
поверх-ной плёнки жидк-ти.
=1;
=F;
=
;
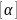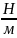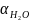=0,073
;
t=20°С;
=0,49
.
Найдём работу, кот. надо соверш., чтобы
увелич. S поверхн-ной плёнки на ΔS
Δ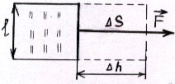
А=ΔhF=Δhα
=αΔS;
α=
.
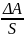Работа ΔА идёт на увелич. внутр. энергии
плёнки (своб. энергии плёнки) α=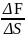
(ΔS=1)
2.
Коэффиц. поверхн. натяж. численно равен
изменению своб. энергии поверхн-ной
плёнки при увелич. её площади на 1.
=
С ростом темпер. α уменьш:1)на языке сил (с ростом темпер. увеличив V жидк-ти и соотв. увеличив. расстоян. между молекулами жидк и значит уменьш. α); 2)на языке энергий(если темпер. растёт, то молекула увелич. свою кинетич. энергию. Молекуле легче проникн. в поверхн-ный слой и роль потенц. энергии уменьш.) Поверх-ный слой жидк-ти аналогичен упругой плёнке по поведению,но есть различия.Натяжение обычной упругой плёнки прямопропорц. деформации плёнки и =0 при некот. конечной площади упругой плёнки. Поверх-ное натяж. жидк. не завис. от размера свободн. пов-ти и стрем-ся сократить его до 0.Это обусловл. тем, что при изотерм. сжат. и расшир. жидких плёнок измен. число молекул, содерж. в плёнке, а средн.расстоян. между молекулами не мен-ся, а потому не меняется и сила поверх-ного сцепл., стремящ-ся сжать плёнку.