64. Теплопроводность. Коэффициент теплопроводности.

Теплопроводность в газе – направленный перенос кинетической энергии молекул за счет хаотичного теплового движения молекул и их сталкивании. При наличии неоднородной температуры, в результате чего происходит выравнивание температур в газе до достижения полного равновесия.

Рассмотрим одномерный случай:

Рассмотрим одноатомный газ и пусть градиент температуры равен

2 предположения, компенсирующие друг друга:

1) будем считать, что в соседних слоях средняя энергия различна, а средняя скорость – одинаковая.

2) концентрация молекул в соседних слоях одинаковая n

Тепловой поток через площадь за время равен:

Тогда тепловой поток проходящий через единицу площади за единицу времени:

Тепловой поток пропорционален градиенту температуры. Знак ‘‘минус’’ – q направлено в сторону убывания температуры. Коэффициент теплопроводности численно равен количеству тепла, проходящего через единицу площади соприкасающихся слоев за единицу времени, при градиенте температуры равном (-1).

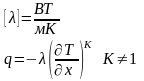
65. Уравнение теплопроводности.

Уравнение теплопроводности описывает процесс переноса тепла в одномерном случае.

Ц илиндр АВ расположен вдоль оси х, плотность газа длина поперечного сечения

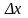
Тепло, поступающее в цилиндр за время dt через основание А равно:

Тепло, выходящее из цилиндра

Тепло, поступающее в цилиндр АВ

С другой стороны это тепло можно представить виде :

dm- масса газа :

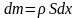
с-удельная теплоемкость :

Приравниваем

В двумерном

К уравнению теплопроводности необходимо задать граничные и начальные условия, тогда приходим к краевой задачи Коши:

66. Вязкость. Коэффициент вязкости.

Я вл. вязкости в газе - это направленный перенос импульса упорядоченного движения молекул за счет их хаотичного движ при наличии градиента скорости упорядочн движ

Импульс упорядочен. движ равен переносимый через ∆S:

По 2 закону Ньютона: изменение импульса слоя = импульсу силы трения, действ за в направлении скор параллельной

т.е. Fтр =

fтр = =

Закон Внутр трения(вязкости) Ньютона:

fтр= - ; η – к-т динамической вяз-ти

Сила внутр тр при макроскопич движении газа пропорциональна градиенту скор газа упорядочн движ. Возникает за счёт переноса импульса. Коэффициент вязкости численно равен силе внутр тр, на ед S при градиенте скор = -1,

Киниматич коэф вязкости есть динамич дел на

, [м² /с]

Не Ньтоновская вязкость жидкости:

67. Фазовые равновесия и превращения. Фазы и фазовые превращения.

Ф азой наз. Макроскопическое физически однородная часть вещества, отделенная границами от остальн части сист. В сист может быть несколько ТВ и жидк фаз, но газообразн только 1. Различн фазы явл агрегатн сост вещва (ж, т, г). Фаза - более широкое понятие, чем агрегатное сост вещва могут сущ различн фазы одного агр сост. Различн фазы одного и того же вещва могутнаходиться в тепловом и механич равновесии. При тепловом равновесии темпер фаз одинакова, при механич равновес существование 2 фаз возможно при опр знач t и p. Переход вещва из 1 фазы в 2 – это фазовый переход. Различают фазовый переход 1 и 2 –го рода. Примеры: сублимация, испарение, кристаллизация, плавление.

Р авновесие 2 фаз возможно только вдоль определённой линии: p = p(t). Равновесие 3 фаз – в одной точке (тройной):

t_тр = 0,01^оС

p_ТР = 4,62 мм рт ст

возможно существование нескольких тройных точек.

Фазовый переход 2-го рода не связаны с теплотой фаз перехода, они связаны с модификацией кристалл решетки при этом могут меняться скачком такие характеристики: теплоемкость, коэф тепл расшир

Фазовый переход 2-го рода, пример:

1. Переход некоторметаловпри сверхнизких темпер в сверх проводящ расстояния

2. Переход ферромагнетика железа в обычн паростаметик со слабым магн свовами.

Переход Гелий 1 в Гелий 2 (где энта=0)