59.Принцип возрастания энтропии

П усть сис-ма переходит из сост.1 в сост. 2 по пути I необрат. образом:

А из сост 2 в сост.1 переход. По пути II обратимым образом. В силу неравенства Клаузиуса имеем ;

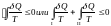Пусть переход по пути I теплоизолирован

-принцип возрост энтропии

Энтропия изолир-ой сис-мы не убывает. Она либо возрост. При необрат. процессах либо остаётся постоянной при обратимых. Тогда приходим к 5-ой форм-ке 2-го НТ:

5) Реальные в изолир. сис-ме протекает в сторону возрост. энтропии.

12) Если сис-ма теплоизолир-на, но не изолир-на информационно, то закон возрост. Энтропии с учётом притока инф. ∆I принимает вид: ∆S + ∆I ≥ 0.

Если термосист-ма не изолир-на, то S такой сис-мы может и убывать. Открыт. Сис-мы, кот. характеризуются отриц S, характ. живые сущ-ва. Клаузис выдвинул гипотезу: Энергия мира остаётся постоянной, а энтропия мира стремится к максимуму. В силу 2-го НТ энтропия нашего мира возрастает.

60. Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.

Все тепловые явления являются необрат. По этому необратимость тепловых явлений противоречит обратимости тепловых движений атомов и молекул. Необратимость тепловых явлений носит статистический вероятностный характер. Сост макроскопической сис-мы можно характ-ть двояко

1) сост. Сис-мы заданное набором термодинам-х параметров p,V, T, n- это макросостояние

2) сост. Сис-мы при задании всех координат и всех импульсов составл. сис-му наз микросостоянием

Статистическим весом или термодинамической вероятностью наз. число микросост. соответств. Данному макрососоянию.

Переход сис-мы из неравновесного сост. В равновесное представл. собой переход, кот. Осуществл-ся несравнимо большим числом микросостояний чем обратный переход. По этому необратимость тепловых процессов носит вероятностный характер. Вероятность того, что молекула будет находится в первой части сосуда = ½, 2 молекулы =1/4, 3 – 1/8

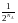
Число W характ. данное макросост предтавл собой степень беспорядочности макросост. При равновероятн микросост чаще будут осущ те макросост кот соотв большее число микросост, т.е. кот будут иметь больший статист-ий вес W, что соотв большей неупорядочности сис-мы. Больцман устан связь S и W : . Пусть сис-ма разбита на 2 слабовзоимод подсис-мы 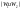, тогда число допуст состояний всей сис-мы равно 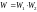. Больцман предположил, что энтропия S – есть универс функция сис-мы, т.е. , тогда для подсис-м .

В силу аддетивности энтропии имеем .

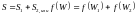Решением последнего функционального ур-я явл выражение

;

Покажем, что k – постоянная Больцмана, k=1,38·10²³ Дж/К, действительно: пусть 1 моль газа расшир в вакууме. Число возможн микросост для одной молекулы прямопропорционально объёму сис-мы. Т.к 1 моль газа содержит -молекул, то число возможн. микросост W пропорционально , тогда S сис-мы будет равна .

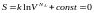Пусть газ очень медленно расшир в вакуум от объёма до 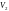, тогда увелич S будет равно .

С другой стороны изм S одного моля газа при изотерм-м процессе:

.

Славнивая последние выраж, приходим, что k – постоянная Больцмана.

;

16) 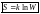(ф-ла Больцмана) -Энтропия сис-мы прямопропорциональна логарифму натуралному термодинам-кой вероятности состояний. Процесс явл необратимым, если обратный ему процесс крайне маловероятен. Например: расшир газа в вакуум необрат. По-скольку энтропия имеет вероятностный характер, то такой характер преобр IIНТ. Наиболее вероятным изм-м энтропии явл её увеличение(уточн. 6-ой фор-ки IIНТ).

6) В замкнутой сис-ме наиболее вероятны такие процессы, когда энтропия возростает. Впринципе возожны такие прцессы, при кот энтропия замкнутой сис-мы убывает, но вероятность таких процессов очень мала. Процессы уменьш S в замкнут сис-мах возможны в флуктуациях (-это случайные отклон наблюд-х физич-х величин от их равновесных статист. Средних) Флуктуации возник за счёт хаотического характера движ молекул. Можно показать, что относ-я флуктуаци обратнопропорц-на корню кв-му из числа молекул N: ∆V/V~1/√N

17) Хаотическому сост сис-мы соотв-т наибольший статист-ий вес W, по этому S=klnW – есть мера хаотичности сис-мы. IIНТ не носит обсолютный характер, в отличии от I и для IIНТ возможны отклонения. Расм. III НТ: «Пусть абсол. 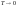, тогда сис-ма как првило будет нах-ся в осн квантово-мех-ом сост-ии, при кот достиг-ся полная упорядоченность сис-мы (квантовый кристалл). Это сост-е осущ-ся в отсутсвие вырождения единственным образом». W=1, тогда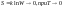 , тогда приходим к IIIНТ или тепловой теореме Нернста: «энтропия сис-мы при обсалютном нуле обращается в ноль». Покажем теперь недостижимсть абсол-го нуля температуры.Действительно: пусть абсол-ый ноль темпер-ры достижим, тогда КПД машины 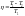и если Т₂=0, то , что противоречит IIНТ

( <1).