57. Второе начало термодинамики (6 формулировок).

Второе начало термодинамики указывает направление протекания термодинамических процессов. Оно было установлено при анализе работы тепловой машины Карно в 1824г.

Существует более 10 формулировок второго начала, они эквивалентны:

1) Невозможен процесс единственным конечным результатом, которого является переход тепла от тела менее нагретого к более нагретому или, короче говоря, тепло самопроизвольно, т. е. без совершения работы не может переходить от холодного к горячему телу (Клаузиус)

2) Невозможен процесс единственным конечным результатом которого является превращение всей теплоты полученной от нагревателя в эквивалентную ей работу (Кельвин-плант)

3) КПД тепловой машины всегда строго меньше 1.

4) Невозможен вечный двигатель второго рода – это периодически действующий двигатель, получающий тепло от одного резервуара и полностью превращать это тепло в работу.

5) Реальные процессы в изолированной системе протекают в сторону возрастания энтропии.

6) В замкнутой системе наиболее вероятные такие процессы, когда энтропия возрастает.

58. Энтропия

КПД реальной тепловой машины при необрат. процессах:

=

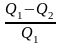
КПД обрат. процесса : =

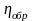Т.к. при необрат. процессах часть тепла теряется, то ≤

≤

И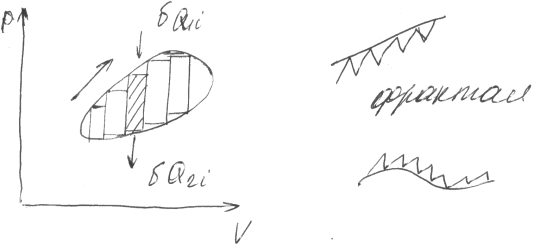 ли преобразовав это неравенство можно получить Неравенство Клаузиса: ; - приводимое кол-во тепла.

Любой круговой процесс можно представить как совокупность бесконечно малых циклов Карно

Тогда нер-во Клаузеса можно записать для i-того прцесса

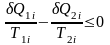
Просуммировав по всем циклам Карно:

Пусть число разбиений на циклы Карно стремится к ∞, тогда в пределе

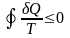
Для обратимых круговых процессов имеем знак равенства 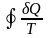= 0

Известно, что если интеграл по замкнутому контуру от нек-ой функции = 0, то подынтегральное выраж-е – есть полный дифф-л нек-ой функции S, т.е.

1)

2) Сущ. функция S состояния сис-мы, кот. подобно внутр. энергии не зависит от формы траектории и эта функция состояния сис-мы наз энтропией сис-мы.

3) Значение энтропии S для каждого сост-я опред-ся с точностью до аддитивной постоянной (важнее роль значения не S, а dS).

4) Для обрат. процессов изменение S сис-мы =

5) Единица измерения энтропии: [S]=Дж/К

6) По характеру изм. S можно судить о направлении протек-я процессов:

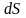Т >0, , > 0, > 0 - сис-ма получает тепло. Если сис-ма получает тепло, то энтропия её увелич. Если < 0, < 0, сис-ма отдаёт тепло.

7) По самому определ. энтропии она явл-ся аддитивной величиной, т.е. энтропия сис-мы равна сумме энтропий её частей.

8) При обратимом процессе , а если процесс ещё и адиабатный, то = 0 → = 0, S = const, по этому адиабатический процесс - есть изэнтропический. Обратим. адиабата - есть изентропа.

9) 1 и 2-ое НТ записанные совместно приводят к осн. Термодинамическому тождеству: ,

10) Найдём изм. S идеального газа при переходе его из сост. 1 в сост. 2 обратимым образом: ;

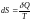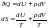, по скольку ; ; ;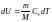

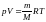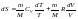
-изменение энтропии

Если расм. изотерм-ий переход, когда - .

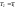Пусть два тела с различными температурами приведены в соприкосн и пусть вырав-е темпер-ры происходит медленно:

.

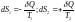
11) Покажем, что энтропия есть мера обесцененности внутр энергии сис-мы. Основное термодинам-е тождество:

или ;

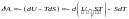Пусть процесс явл. изотермическим ; .

Тогда свободная энергия F сис-мы есть мера той работы, кот сис-ма может совершить в обратимом изотермич-ом процессе. Т.к. внутр энергия сис-мы , то внутр энергия – есть сумма своб энергии F и связанной энергии TS. Энергия TS – есть та часть внутр энергии, кот не может быть превращена в работу. Эта связанная энергия TS тем больше, чем больше энтропия S. Отсюда S – есть мера обесцененности внутр энергии сис-мы, т.е. эта та часть энергии, кот не может быть обращ в работу