55. Цикл Карно. Максимальный кпд тепловой машины.

В термодинамике широко используется 2 основных метода:

1) Метод круговых процессов (циклов). Метод широко использовался Карно, Клаузиусом, Нернстом.

2) Метод термодинамических потенциалов (характеристических функций), применялся Гиббсом.

Метод циклов обычно используют в технической термодинамике для расчета КПД, для изучения газов и паров, для изучения течения паров в турбинах. Метод термодинамических потенциалов используют в химической термодинамик при изучении свойств жидкостей и твердых тел, при изучении фазовых превращений Цикл Карно – обратимый круговой процесс состоящий из двух изотерм и двух адиабат. Машина, работающая по циклу Карно, называется машиной Карно (идеальная тепловая машина). Изобразим цикл Карно на диаграмме pV:

Н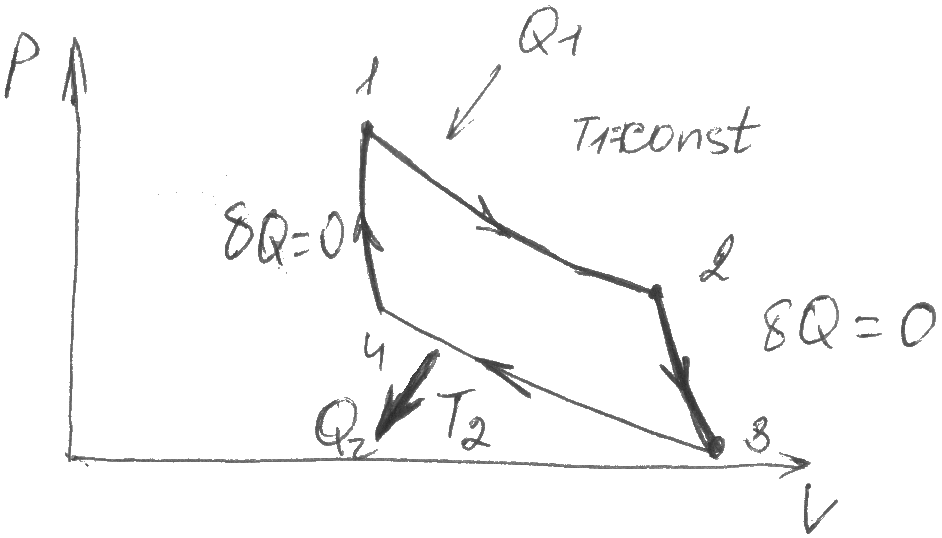 а уч-ке 1-2 газ получает тепло Q₁ и изотермически расширяется при Т₁=const. 2-3 газ адиабатно расшир. 3-4 газ отдает тепло Q₂ и изотермически сжим-ся при Т₂= const. 4-1 газ адиабатно сжимается δQ=0

Найдем КПД цикла Карно:

η=(Q₁- Q₂)/ Q₁ (1)

Пусть рабочее тело машины Карно идеальный газ, тогда : Q₁=А_1-2=m/M*RT₁lnV₂/V₁ (2)

На участке 3-4 тепло отдается (-Q₂)

Q₂=А_3-4=m/M*RT₂lnV₄/V₃ (3)

Что бы цикл был замкнутым надо, что бы состояния 2 и 3 лежали на одной адиабате

2,3 Т₁V₂^γ-1=T₂V₃^γ-1 (4)

Совершенно аналогично для состояний 1и 4

1,4 Т₁V₁^γ-1=T₂V₄^γ-1 (5)

Поделим теперь 4 на 5 и извлечем ^γ-1√:

V2/V1=V3/V4 (6)

подставим теперь (2), (3), в (1) и учтем (6)

η=(Т₁- Т₂)/ Т₁ - КПД цикла Карно

КПД цикла Карно равен отношению разности температур нагревателя и холодильника к абсолютной температуре нагревателя.

Теорема Карно: «КПД обратимой тепловой машины Карно не зависит от ее устройства и свойств рабочего вещества, а определяется только абсолютными температурами нагревателя (Т₁) и холодильника (Т₂)».

56. Технические циклы.

Наибольшим КПД обладает цикл Карно, но практически такой цикл осуществить не возможно т. к. происходит очень медленно, поэтому разработано большое количество технических циклов.

А) Циклы поршневых тепловых двигателей:

1) Цикл Отто, сгорание при постоянном объёме (V= const)

Изобразим этот цикл на диаграмме pV:

1 -2 адиабатическое сжатие

2-3 изохорное нагревание

3-4 адиабатное расширение

4-1 изохорное охлаждение

η=(Q₁- Q₂)/ Q₁

Первое начало термодинамики: δQ=dU+pdV

На 2-3, 4-1 dV=0 и следовательно δQ=dU

Q₁=νC_V(T₃-T₂) ; Q₁=νC_V(T₄-T₁)

Подставим Q₁ и Q₂ в КПД, получаем:

η=((T₃-T₂)- (T₄-T₁))/ (T₃-T₂)

Воспользуемся теперь, что точки 3 и 4 лежат на одной адиабате:

3,4 T₃V₂ ^γ-1= T₄V₁ ^γ-1

Точки 1и2 лежат на одной адиабате

1,2 T₁V₁ ^γ-1= T₂V₂ ^γ-1

Перемножим два последних соотношения:

Т₁Т₃=Т₄Т₂ следовательно Т₄=Т₁Т₃/Т₂

Подставим Т₄ в η:

η=((T₃-T₂)- ((Т₁Т₃/Т₂)-T₁)/ (T₃-T₂) , упрощая получаем:

η=1 - Т₁/Т₂ - получаем выражение для цикла Отто, его часто записывают в другом виде. Введем коэффициент сжатия ε =V₁/V₂

С использованием уравнения адиабаты для участка 1-2 получаем выражение цикла Отто:

η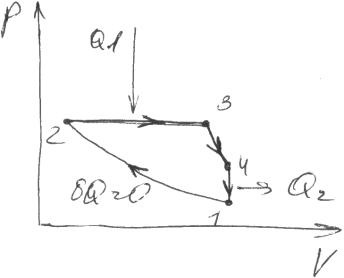 =1 - 1/ ε ^γ-1

2) Цикл сгорания с р =const (Дизель)

1-2 адиабатное сжатие

2-3 р = const

3-4 адиабатное расширение

4-1 V = const

Б) Циклы газовых турбин:

1) Цикл сгорания с V=const

1-2 адиабатное сжатие

2-3 V = const

3-4 адиабатное расширение

4-1 р = const

2) сгорание при p=const.

1 -2 адиабатное сжатие

2-3 р = const

3-4 адиабатное расширение

4-1 р = const