- •1О. Кинематика поступательного движения.
- •2О. Кинематика вращательного движения.
- •3О. Динамика частиц. Закон ньютона.
- •4О. Неинерциальные системы отсчета (нсо). Силы инерции.
- •5О. Основное ур-ние динамики вращательного движения тв. Тела.
- •7О. Закон сохранения импульса.
- •8О. Работа.Мощность.Кинетическая энергия системы.
- •9О. Потенциальная энергия системы.
- •10. Закон сохранения энергии в механике
- •11О. Закон сохранения момента импульса.
- •12О. Движение тела переменной массы.
- •13О. Кинематика гарманических колебаний
- •14О. Гармонический осциллятор.
- •15О. Примеры гармонических осцилляторов.
- •16. Сложение гармонических колебаний одного направления и частоты.
- •17. Сложение взаимно перпендикулярных гармонических колебаний.
- •18. Затухающие колебания.
- •19.Вынужденные колебания. Резонанс.
- •20.Упругие волны в средах.
- •21О.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.
- •22. Одномерное волновое ур-е. Энергия волны.
- •23. Распространение волн в средах с дисперсией. Групповая скорость, ее связь с фазовой скоростью.
- •24. Стоячие волны
- •25. Элементы акустики.
- •26.Модуль Юнга. Скорость звука.
- •28. Постулаты сто. Преобразование
- •29. Средства преобразования Лоренца.
- •30. Релятивистский закон сложения скоростей.
- •31. Интервал между событиями и его инвариантность в преобразовании Лоренца
- •32. Релятивистская динамика, кинетическая энергия сто.
- •33. Связь массы, энергии, импульса в сто
- •34О. Эффект Доплера
- •35О. Принцип эквиваленности.Понятие о ото
- •36О. Равновесие и течение жидкости и газа
- •37О. Уравнение неразрывности струи. Уравнение Бернулли
- •38. Уравнение Эйлера. Движение идеальной жидкости.
- •39. Течение вязкой жидкости. Формула Стокса.
- •40. Течение вязкой жидкости в трубах. Формула Пуазейля.
- •41. Динамический и статистический закономерности в физике.
- •42. Уравнение состояния идеального газа.
- •43. Основное уравнение молекулярно-кинетической теории газов (мкт).
- •44. Молекулярно-кинетический смысл абсолютной температуры.
- •45. Распределение Максвелла.
- •46. Параметрическая формула распределения Больцмана.
- •47. Распределение Гиббса.
- •48. Первое начало термодинамики.
- •49. Теплоемкость многоатомных газов.
- •50. Применение I начала термодинамики к изопроцессам(термодинамическим процессам).
- •51. Адиабатический процесс.
- •52. Политропный процесс
- •53. Теплоемкость и работа газа в политропном процессе
- •54. Обратимые и необратимые процессы, круговой процесс, тепловые двигатели, холодильные машины.
- •55. Цикл Карно. Максимальный кпд тепловой машины.
- •56. Технические циклы.
- •57. Второе начало термодинамики (6 формулировок).
- •58. Энтропия
- •59.Принцип возрастания энтропии
- •60. Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.
- •61. Метод термодинамических потенциалов (характеристических функций).
- •62. Явления переноса. Средняя длина свободного пробега молекул.
- •63. Коэффициент диффузии.
- •64. Теплопроводность. Коэффициент теплопроводности.
- •65. Уравнение теплопроводности.
- •66. Вязкость. Коэффициент вязкости.
- •67. Фазовые равновесия и превращения. Фазы и фазовые превращения.
- •68. Уравнение Клайперона - Клаузиса.
- •69. Реальные газы. Уравнение Ван – дер - Вальса .
- •70. Изотермы Ван-дер-Ваальса. Критич. Состояние. Внутр. Энергия реального газа.
- •71. Твёрдые тела.Теплоёмкость кристалла
- •72. Жидкости.Поверхн. Натяж. Жидк.
- •73. Смачивание и капиллярные явления
- •74. Принцип динамич. Отопления
- •75. Элементы физики полимеров
- •1О. Кинематика поступательного движения.
51. Адиабатический процесс.
Адиабатич. – проц., протекающ. в сист. без теплообмена с окруж. средой. δQ=0
На практике адиабатическ. явл. быстро протекающ. проц.,не успевающ. установить теплообм. с окр. средой. I НТД(начало термодинамики) для адиабатич. проц.: dU+ δA=0
δA= -dU работа газа в адиабатном проц. соверш. тока за счет внутр. энерг. газа.
Получим ур-ние адиабаты, исходя из I НТД:
dU+ δA = 0
VdT+ pdV = 0 ; p =
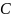 VdT
+
VdT
+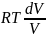 = 0 ||
= 0 ||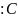 VT
;
VT
;
 +
+
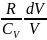 = 0
= 0
Интегрир. обе части последн. ур-ния:
 +
+
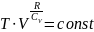
R=Cp-CV формула Майера
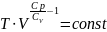
γ
= ;
;
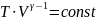
Получим теперь уравнение адиабаты впеременных p и V для идеального газа:
pV=
T=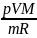
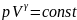
На диаграмме p и V адиабата идет круче,чем изотерма. Получим выраж. для работы в адиабатном проц.:
δA= -dU ; δA= - VdT
A=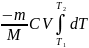 ; A=
V
(T1-T2)
; A=
V
(T1-T2)

52. Политропный процесс
Политропный – процесс,протекающ. при постоян. теплоемкости. C=const.
Получим ур-ние полинтропы для идеального газа: I НТД имеет вид:
δQ=dU+δA
ν= 1 моль
δQ=CdT
; C= ; dU=
VdT
; δA=pdV
; dU=
VdT
; δA=pdV
CdT= VdT+ pdV ; (C- V )dT= pdV
Воспользуемся тем, что газ идеальный: Ур-ние сост. идеального газа для 1 моля:
d|| pV=RT ; pdV+Vdp=RdT
dT=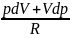
(C- V ) ) = pRdV
(C-
V
–R)pdV+(C-
V
)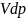 =0
||: p(C-
V
)V
=0
||: p(C-
V
)V
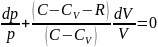
Проинтегрируем:
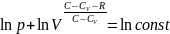
Потенцируя (обр. операц. логарифмиров.)
 =const
; Cp=CV+R
;
=const
; Cp=CV+R
;
 =const
=const
Введем индекс политропы:
n
=
 ур-ние политропы
ур-ние политропы
Политропный проц. включ. в себя как частн. случаи все виды изопроц.
n |
Вид изопроцесса |
С вид теплоемкости |
0 |
p=const изобарный |
Cp |
1 |
pV=const изотермичский |
C |
γ |
адиабатный |
0 |
|
V=const изохорный |
CV |
Изобразим изопроцессы на плоскости p и V

53. Теплоемкость и работа газа в политропном процессе
Индекс политропы n =
nC-nCv=C-Cp ; (n-1)C= nCv- Cp
C=
Cv
Е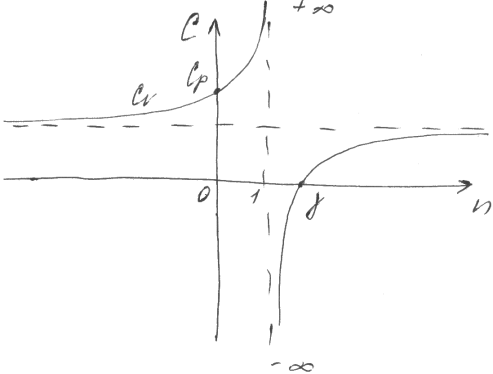 сли
1< n
<γ,
то C
<0 теплоемк. может быть отрицательной;
если n
= γ,
С = 0 адиабатный процесс; C>0,
если n>γ,
n>1;
0<n<1
сли
1< n
<γ,
то C
<0 теплоемк. может быть отрицательной;
если n
= γ,
С = 0 адиабатный процесс; C>0,
если n>γ,
n>1;
0<n<1
Зависимость теплоемкости от индекса политропы:
Вычислим работу в политропном процессе:
Имеем:
 откуда
откуда

Тогда элементарная работа будет равна:
δA= dV
dV
A12=
I=
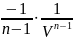
С учетом ур-ния сост. идеального газа имеем:
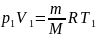
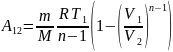 n
n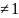
работа газа в политропном процессе при n
n=1

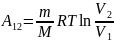
54. Обратимые и необратимые процессы, круговой процесс, тепловые двигатели, холодильные машины.
В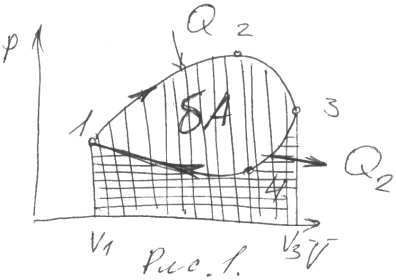 сякий
термодинамический процесс есть переход
системы из одного состояния в другое и
такой переход связан с нарушением
равновесия системы. Равновесный
процесс - процесс, состоящий из
непрерывной последовательности
равновесных состояний. Такие процессы
на диаграмме состояния изображаются
сплошной линией. Равновесным может быть
только бесконечно медленный процесс.
Обратимые процессы – процесс который
допускает возвращение системы в исходное
состояние, так что система может
переходить через те же промежуточные
состояния но в обратной последовательности,
при этом, возвращаясь в исходное
состояние, тела взаимодействуют с
системой. Обратимые – бесконечно
медленное расширение, сжатие газа.
Необратимые – расширение газа в
вакууме, явления теплопроводности,
диффузии. Как правило все процессы
необратимы. Круговым процессом(циклом)
называется равновесный процесс, при
котором система после ряда изменений
возвращается в исходное состояние.
Изобразим цикл на диаграмме pV:
На участке 1-2-3 газ расширяется, при
этом, получая некоторое количество
тепла (Q1) и совершает
работу, численно равную площади
вертикально заштрихованной фигуры. На
участке 3-4-1 газ сжимается и совершает
отрицательную работу, или над газом
совершается положительная работа, при
этом от газа отводится некоторое
количество тепла(Q2).
Работа совершаемая над газом численно
равна площади горизонтально заштрихованной
фигуры. После выполнения цикла газ
возвращается в исходное состояние
(dU=0) и 1-ое начало термодинамики
имеет вид: δQ=δA
; Работа δA численно
равна площади фигуры 1-2-3-4, а
сякий
термодинамический процесс есть переход
системы из одного состояния в другое и
такой переход связан с нарушением
равновесия системы. Равновесный
процесс - процесс, состоящий из
непрерывной последовательности
равновесных состояний. Такие процессы
на диаграмме состояния изображаются
сплошной линией. Равновесным может быть
только бесконечно медленный процесс.
Обратимые процессы – процесс который
допускает возвращение системы в исходное
состояние, так что система может
переходить через те же промежуточные
состояния но в обратной последовательности,
при этом, возвращаясь в исходное
состояние, тела взаимодействуют с
системой. Обратимые – бесконечно
медленное расширение, сжатие газа.
Необратимые – расширение газа в
вакууме, явления теплопроводности,
диффузии. Как правило все процессы
необратимы. Круговым процессом(циклом)
называется равновесный процесс, при
котором система после ряда изменений
возвращается в исходное состояние.
Изобразим цикл на диаграмме pV:
На участке 1-2-3 газ расширяется, при
этом, получая некоторое количество
тепла (Q1) и совершает
работу, численно равную площади
вертикально заштрихованной фигуры. На
участке 3-4-1 газ сжимается и совершает
отрицательную работу, или над газом
совершается положительная работа, при
этом от газа отводится некоторое
количество тепла(Q2).
Работа совершаемая над газом численно
равна площади горизонтально заштрихованной
фигуры. После выполнения цикла газ
возвращается в исходное состояние
(dU=0) и 1-ое начало термодинамики
имеет вид: δQ=δA
; Работа δA численно
равна площади фигуры 1-2-3-4, а
δQ= Q1- Q2 ; Прямым циклон называется равновесный круговой процесс, когда расширение газа происходит при давлениях больших, чем при сжатиях, т. е. на диаграмме pV такой цикл происходит в направлении движения часовой стрелки. В прямом цикле работа газа положительна и по такому циклу работают тепловые машины, при этом работа (δA) совершается за счет тепла (δQ) сообщенного газу. Обратный цикл протекает в направлении противоположном движению часовой стрелки, по обратному циклу работают холодильные машины, тогда работа газа отрицательна и от газа отводят некоторое количество тепла.
Тепловой машиной называют периодически действующий двигатель, совершающий работу за счет тепла получаемого из вне.
Основные элементы тепловой машины:
--нагреватель
--рабочее тело \ вещество
--холодильник
Пусть Q1 это тепло получаемое от нагревателя рабочим телом на участке1-2-3 , Q2 – тепло возвращаемое рабочим телом холодильнику, тогда на работу затрачивается тепло
δQ= Q1- Q2 Вводится КПД (η) – отношение полезно использованного тепла (Q1- Q2) к теплу Q1 полученного от нагревателя. η=(Q1- Q2)/ Q1 η = δA/ Q1
КПД – отношение механической работы совершаемой тепловой машиной за один цикл к количеству тепла отнятого от нагревателя.
КПД паровоза 7%, трансформатора 98% η не больше 1
Холодильный коэффициент (ε) применяется для характеристики цикла при котором происходит перенос тепла от холодного к горячему телу. Холодильный коэффициент – отношение тепла (Q2) отнятого от охлаждаемого тела к работе (А) затрачиваемой на приведение машины в действие: ε = Q2/А= Q2/ Q1- Q2 ε > 1
Холодильная машина отбирает за один цикл от тела с температурой Т2 количество тепла Q2 и отдает телу с более высокой температурой Т1 количество тепла Q1, для обратимого обратного цикла Карно холодильный коэффициент максимален и равен: ε =Т2/(Т1-Т2)